Презентація на тему "Основні співвідношення між тригонометричними функціями одного аргументу"
Про матеріал
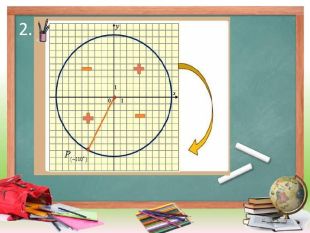
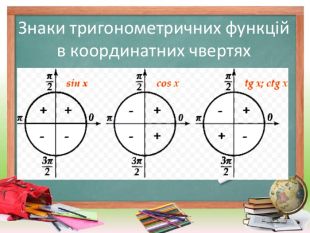
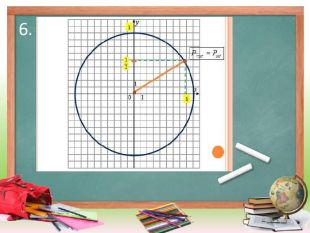
Використано різноманітні форми й методи організації роботи, створюючи атмосферу зацікавленості кожного учня до вивчення теми. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку