Розробка уроку на тему "Теорема Фалеса."
Тема. Теорема Фалеса
Мета: формувати в учнів усвідомлене розуміння змісту теореми Фалеса та способу її доведення; формувати вміння відтворювати формулювання теореми Фалеса; застосовувати її для розв'язування задач на знаходження довжин відрізків, що відтинаються на сторонах паралельними прямими; розв'язувати задачі на поділ відрізка на п рівні відрізки або в даному відношенні.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Теорема Фалеса».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
На цьому етапі уроку можна провести самостійну роботу, зміст завдань якої відтворює ситуацію, опрацьовану на попередніх уроках (застосування властивостей рівнобічної трапеції разом із властивістю катета, що лежить проти кута 30°).
Самостійна робота
Варіант 1
- Основи рівнобічної трапеції дорівнюють 9 см і 15 см. Знайдіть відрізки, на які ділить більшу основу висота, проведена з вершини тупого кута.
- У рівнобічній трапеції один з кутів дорівнює 120°. Діагональ трапеції утворює з основою кут 30°. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 8 см.
Варіант 2
- Основи рівнобічної трапеції дорівнюють 2 см і 10 см. Знайдіть довжини відрізків, на які висота трапеції, проведена з вершини тупого кута, ділить більшу основу.
- У рівнобічній трапеції одна основа дорівнює а, друга втричі менша. Кут при більшій основі дорівнює 60°. Визначте периметр трапеції.
Після виконання завдань самостійної роботи вчитель збирає зошити учнів для перевірки та опрацювання (причому можна оцінити як домашню, так і самостійну роботи та порівняти оцінки). Але обов'язковою умовою має бути надання учням можливості дізнатися, який вигляд має правильне розв'язання завдань — для цього вчитель заздалегідь готує записи правильного розв'язання завдань самостійної роботи або за дошкою, або у вигляді роздавального матеріалу. У разі необхідності розв'язання задач обговорюються. Учням, які не впоралися із завданнями, надається можливість виконання коригуючої роботи (на одному з наступних уроків у вигляді індивідуального завдання).
III. Формулювання мети і завдань уроку
Оскільки властивість середньої лінії трапеції не випливає безпосередньо з теореми Фалеса, то вчитель формулює мету цього та наступного уроків без залучення учнів. Учням повідомляється про існування ще одного з відрізків трапеції, що має важливу властивість (мається на увазі перша середня лінія трапеції), доведення якої ґрунтується на теоремі, яку учні вивчатимуть на уроці. Отже, метою цього уроку є вивчення змісту, доведення та вивчення способів застосування однієї з найважливіших теорем курсу геометрії 7—12 класів — теореми Фалеса.
IV. Актуалізація опорних знань
З метою підготовки учнів до свідомого розуміння та способу доведення теореми Фалеса слід активізувати знання і вміння учнів щодо ознак паралельності прямих, властивості паралельних прямих, означення та властивостей паралелограма, ознак рівності трикутників.
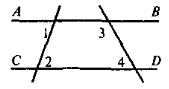
Виконання усних вправ за готовими рисунками
|
1 |
|
Дано:
Довести: |
|
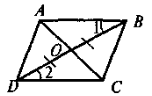
2 |
|
Дано: ВО = ОD, |
|
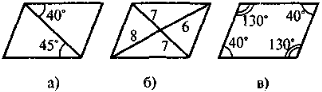
3
|
|
Які помилки допущено в зображенні паралелограма |
V. Засвоєння знань
План вивчення нового матеріалу
- «Класичне» формулювання і доведення теореми Фалеса.
- інше формулювання теореми Фалеса.
- Задача про поділ відрізка на п рівних частин.
Формулювання і доведення теореми Фалеса, що подано в новому підручнику, не відрізняється від аналогічного матеріалу попередніх підручників геометрії. За змістом і за формою розгляд теореми Фалеса повністю відповідає підручнику О. В. Погорєлова. Тому під час викладення цього матеріалу вчитель може використовувати ті самі прийоми і форми роботи, що й раніше. А саме:
- сформулювавши теорему, спочатку попрацювати над усвідомленням учнями самого змісту (важливо, щоб учні усвідомили, що для виконання умови, записаної у висновку теореми, необхідне виконання трьох умов: прямі мають бути паралельні, прямі мають перетинати обидві сторони кута, паралельні прямі мають відтинати на одній зі сторін рівні відрізки); для цього пропонуємо учням виконати усні вправи (див. нижче);
- оскільки доведення теореми є досить простим (ґрунтується на знайомих учням означенні та властивостях паралелограма, а також на ознаках рівності трикутників), то доведення теореми учні можуть розглянути самостійно за підручником. Для усвідомлення ними змісту та логіки доведення вчитель може запропонувати на етапі роботи із доведенням, поданим у підручнику, скласти його план;
- після цієї роботи вчитель пропонує учням «пофантазувати» за теоремою Фалеса: чи буде вона виконуватись, якщо паралельні прямі, що перетинають сторони кута, відтинають кілька рівних відрізків на одній зі сторін кута? Чи буде виконуватися теорема Фалеса, якщо паралельні прямі перетинають не сторони кута, а дві будь-які прямі? Чи буде виконуватись умова, аналогічна до теореми Фалеса, у випадку коли паралельні прямі перетинають сторони не одного, а кількох кутів із спільною вершиною? У випадку ствердної відповіді слід сформулювати «скориговану» для певного випадку теорему (під час обґрунтування своєї точки зору, відповідаючи на поставлені запитання, учні відтворюють міркування, аналогічні до тих, що містяться в доведенні теореми Фалеса, і тим самим закріплюють знання схеми доведення теореми Фалеса);
- як один із засобів застосування вивченої теореми або за підручником, або самостійно учні відшукують спосіб розв'язання класичної задачі на поділ даного відрізка на я рівних частин (перед розв'язуванням цієї задачі для створення проблемної ситуації пропонуємо учням задачу про поділ відрізка на 2п частин, потім пропонуємо випадок, коли п = 3; таким чином учні усвідомлюють неможливість розв'язання задачі відомим способом та необхідність застосування теореми Фалеса).
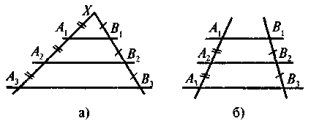
Виконання усних вправ
Дано кут х і прямі АА1, ВВ1, СС1. Заповніть порожні клітинки таблиці: «+» означає виконання умови; «-» означає, що умова не виконується.
|
|
АА1 || ВВ1 || СС1 |
АА1, ВВ1 і СС1 перетинають ХА |
АА1, ВВ1 і СС1 перетинають ХА1 |
АВ = ВС |
А1В1 = В1С1 |
|
1 |
+ |
+ |
+ |
+ |
|
|
2 |
+ |
+ |
- |
+ |
|
|
3 |
- |
+ |
+ |
+ |
|
|
4 |
|
+ |
+ |
- |
+ |
|
Конспект 6 |
|||
|
Теорема Фалеса |
|||
|
|
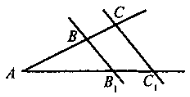
Паралельні прямі, які перетинають дві інші сторони кута і відтинають на одній із них рівні відрізки, відтинають рівні відрізки і на іншій стороні |
||
|
Узагальнена теорема Фалеса |
|||
|
|
|
Паралельні прямі, які перетинають сторони кута, відтинають на сторонах цього кута пропорційні відрізки |
|
VI. Формування первинних умінь
 Оскільки закріплення змісту теореми Фалеса та способу її доведення було здійснено під час вивчення нового матеріалу, то треба почати роботу із формування вмінь та навичок застосовувати теорему для розв'язування задач на обчислення відрізків та доведення їх рівності, а також задач на поділ відрізка на п рівних частин (а також, якщо дозволяє час та можливість учнів, на частини у даному відношенні).
Оскільки закріплення змісту теореми Фалеса та способу її доведення було здійснено під час вивчення нового матеріалу, то треба почати роботу із формування вмінь та навичок застосовувати теорему для розв'язування задач на обчислення відрізків та доведення їх рівності, а також задач на поділ відрізка на п рівних частин (а також, якщо дозволяє час та можливість учнів, на частини у даному відношенні).
Виконання письмових вправ
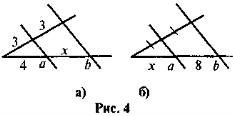
- За даними рисунка 4 знайдіть х, якщо а || b.
-
 Точки М і N — середини сторін ВС і AD паралелограма ABCD. Доведіть, що прямі AM і CN ділять діагональ BD на три рівні частини.
Точки М і N — середини сторін ВС і AD паралелограма ABCD. Доведіть, що прямі AM і CN ділять діагональ BD на три рівні частини.
- Поділіть даний відрізок на шість рівних частин.
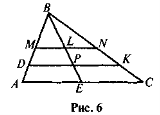
- Точка К — середина медіани AD трикутника ABC (рис. 5). Знайдіть відношення АР : РС.
-
 У прямокутному трикутнику ABC (рис. 6)
У прямокутному трикутнику ABC (рис. 6) 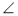 B = 90°, АС = 24 см. МN || АС і DK || AC, ВМ = MA, MD = DA, BE – медіана. Знайдіть LP.
B = 90°, АС = 24 см. МN || АС і DK || AC, ВМ = MA, MD = DA, BE – медіана. Знайдіть LP.
Виконання графічних вправ
Поділіть відрізок у відношенні: а) 1 : 2; б) 2 : 5; в) так, щоб одна з частин становила ![]() відрізка.
відрізка.
VII. Підсумки уроку
Чи правильне твердження: прямі, що відтинають на одній стороні кута рівні відрізки, відтинають на другій його стороні також рівні відрізки? Виконайте відповідні ілюстрації та вставте пропущене слово так, щоб твердження перетворилось на правильне.
VIII. Домашнє завдання
Вивчити зміст та доведення теореми Фалеса, а також алгоритм поділу відрізка на п рівних частин.
Розв'язати задачі.
-
 Через середину D сторони АВ трикутника ABC проведено пряму, яка паралельна АС і перетинає сторону ВС у точці Е. Знайдіть ВС, якщо BE = 8см.
Через середину D сторони АВ трикутника ABC проведено пряму, яка паралельна АС і перетинає сторону ВС у точці Е. Знайдіть ВС, якщо BE = 8см.
- Поділіть відрізок у відношенні 3 : 2.
- Поділіть відрізок на п'ять рівних частин.
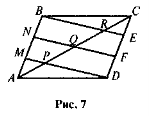
- На стороні АВ паралелограма ABCD (рис. 7) позначили точки М і N, а на стороні CD — точки Е і F так, що BN = NM = MA = CE = EF = FD. Відрізки BE, NF, MD перетинають діагональ АС у точках R, Q, Р відповідно. Доведіть, що AP = PQ = QR = RC.
Повторити означення паралелограма.


про публікацію авторської розробки
Додати розробку