Середня лінія трикутника
Тема. Середня лінія трикутника
Мета: сформувати в учнів поняття середньої лінії трикутника. Розглянути властивості середньої лінії трикутника та зміст задачі Вариньйона; формувати в учнів уміння: відтворювати вивчені твердження (означення та властивості); виконувати зображення середніх ліній трикутника та здійснювати доведення або спростування того, що даний відрізок є середньою лінією трикутника; відтворювати доведення властивості середньої лінії трикутника та опорної задачі; використовувати властивість середньої лінії трикутника під час розв'язування задач.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: конспект «Середня лінія трикутника».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Якщо на попередньому уроці учні добре засвоїли навчальний матеріал, то з метою економії часу на уроці перевірці підлягають тільки завдання достатнього та високого рівнів складності (№ 2, 4). Для цього заздалегідь на дошці виконуються рисунки до цих задач, а на уроці озвучується план розв'язання.
III. Формулювання мети і завдань уроку
Учитель повідомляє учням про те, що розв'язанням задачі на поділ даного відрізка на п рівних частин не обмежується практичне застосування теореми Фалеса. На уроці учні мають засвоїти одне з понять, властивості якого доводяться саме через застосування теореми Фалеса. Засвоєння означення, властивостей та способів застосування цього поняття для розв'язування задачі — головна мета уроку.
IV. Актуалізація опорних знань
З метою підготовки учнів до сприйняття нового поняття та подальшого оволодіння учнями способами дій на застосування нових знань слід активізувати знання і вміння учнів щодо поняття середини відрізка, означення трикутника та його елементів, поняття периметра многокутника, теореми Фалеса, ознак паралелограма.
Виконання усних вправ
|
1 |
|
Знайдіть на відрізки, які є одночасно сторонами не менш як трьох різних трикутників. Назвіть ці трикутники. Чи існують відрізки, які є одночасно сторонами не більш як двох трикутників, зображених на рисунку? |
|
2 |
|
За рисунком складіть задачу і розв'яжіть її |
|
3 |
|
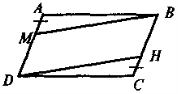
Дано: Довести: АМВН - паралелограм |
|
4 |
|
Дано: ABCD — паралелограм, М — середина ВС, Н — середина AD. Довести: АМСН — паралелограм |
|
5 |
|
Дано: ABCD — паралелограм, AM = СН. Довести: DHBM — паралелограм |
V. Засвоєння нових знань
План вивчення нового матеріалу
- Означення середньої лінії трикутника.
- Властивості середньої лінії трикутника.
- Задача Вариньйона.
Вивчення означення середньої лінії трикутника та її властивостей здійснюється традиційно, але слід урахувати такі контрольні моменти:
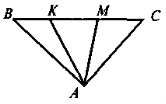
- після введення означення середньої лінії трикутника слід попрацювати над розумінням учнями змісту сформульованого означення (для цього учням пропонується відповісти на запитання: Скільки середніх ліній можна провести в трикутнику? Чи правильне твердження: «Лінія, що з'єднує середини сторін трикутника, є його середньою лінією»? Або виконати усне завдання за готовим рисунком).
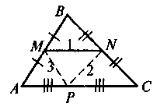
Чи є зображена на рис. 1 лінія середньою лінією трикутника ABC?
- зміст про властивість середньої лінії трикутника слід опрацювати на розуміння (учні мають усвідомити, що в теоремі мова йде про зв'язок між середньою лінією та стороною, до якої вона є паралельною, тобто середня лінія трикутника не дорівнює половині будь-якої його сторони; а також опанувати спосіб визначення середньої лінії за даною паралельною стороною, та навпаки, знаходження сторони, до якої середня лінія трикутника з даною довжиною паралельна);
- доведення як властивості середньої лінії, так і опорної задачі учні можуть опрацьовувати самостійно (скласти план доведення, за якими вдома будуть його вивчати); після вивчення змісту доведення властивості середньої лінії трикутника слід звернути увагу на те, що безпосередньо з доведення (точніше з використання в ньому теореми Фалеса) випливає справедливість твердження про те, що середня лінія трикутника ділить навпіл будь-який відрізок, один кінець якого лежить на паралельній стороні, а другий кінець виходить з протилежної вершини;
- додатково можна розглянути твердження, що безпосередньо випливають із властивостей середньої лінії трапеції (див. конспект, властивості 3, 4).
|
Конспект 7 |
|
|
Середня лінія трикутника |
|
|
|
Означення. Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. |
|
|
|
|
Властивості |
|
|
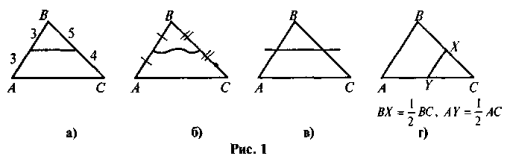
1. У будь-якому трикутнику можна провести 3 середніх лінії.
2. Якщо MN — середня лінія ΔАВС (М — середина АВ, N — середина ВС), то MN || AC, MN = |
|
|
3. Периметр трикутника, утвореного всіма середніми лініями трикутника, дорівнює половині периметра даного трикутника (РΔMNP = |
|
|
4. Три середні лінії трикутника ділять його на чотири рівних трикутники |
|
VI. Формування первинних умінь
Виконання усних вправ
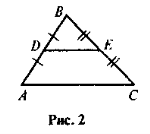
- Відрізок DE — середня лінія трикутника ABC (рис. 2).
а) Визначте вид чотирикутника ADEC.
б) Назвіть медіану трикутника, що виходить з вершини А.
-
 Чи може середня лінія трикутника бути перпендикулярною до його сторони; до двох його сторін?
Чи може середня лінія трикутника бути перпендикулярною до його сторони; до двох його сторін?
- Чи можуть середні лінії трикутника дорівнювати 3 см, 4 см і 10 см? Чому?
- У трикутнику ABC проведено середню лінію паралельно стороні АС. У якому відношенні вона ділить медіану ВМ; висоту ВH?
- Дві середні лінії трикутника рівні між собою і взаємно перпендикулярні. Який це трикутник? Відповідь поясніть.
Виконання графічних вправ
Накресліть трикутник ABC. Позначте на стороні АВ точки А1, А2 і А3 так, щоб вони ділили відрізок АВ на чотири рівні частини. Проведіть через ці точки прямі, паралельні стороні АС, і позначте точки їх перетину зі стороною ВС С1,С2 і С3 відповідно.
а) Виміряйте і порівняйте довжини відрізків, на які точки С1,С2 і С3 ділять сторону ВС.
б) Виділіть червоним кольором середню лінію трикутника ABC.
Виконання письмових вправ
- Сторони трикутника дорівнюють 12 см, 16 см і 20 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника.
- Середня лінія трикутника відтинає від нього трапецію з бічними сторонами 3 м і 4 с і меншою основою 5 м. Знайдіть периметр трикутника.
- Доведіть, що середини сторін ромба є вершинами прямокутника.
Під час розв'язування задачі № 3 слід повторити ознаку прямокутника та використати задачу Вариньйона.
Задача Вариньйона. Середини сторін чотирикутника є вершинами паралелограма.
VII. Підсумки уроку
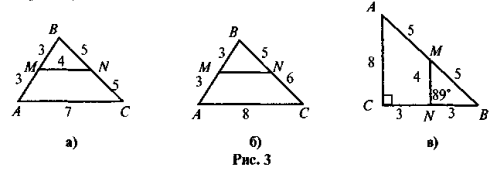
Які помилки допущено в зображенні середньої" лінії трикутника (див. рис. 3)?
VIII. Домашнє завдання
Вивчити зміст нового теоретичного матеріалу. Розв'язати задачі.
-
Накресліть трикутник ABC. Позначте точки D, Е і F — середини
сторін АВ, ВС і АС відповідно. Сполучіть позначені точки.
а) Визначте вид чотирикутника ADEF.
б) Визначте вид чотирикутника ADEC.
в) Назвіть усі трикутники, що дорівнюють трикутнику DEF. Запишіть відповідні рівності.
- Середня лінія рівностороннього трикутника дорівнює 3,5 см. Знайдіть периметр трикутника.
- Діагоналі чотирикутника дорівнюють 18 см і 22 см. Знайдіть периметр паралелограма, вершинами якого є середини сторін даного чотирикутника.
- Доведіть, що середини сторін прямокутника є вершинами ромба.

про публікацію авторської розробки
Додати розробку