Розробка уроку на тему "Теорема Фалеса" (8 клас).

Тема уроку. Теорема Фалеса.

Мета уроку. Засвоєння теореми Фалеса, формування вмінь застосовувати теорему при поділі відрізка на рівні частини та узагальнювати свої теоретичні знання, планувати відповідь. Розвивати логічне мислення (послідовність, доказовість, пошуковість), формування пізнавальної культури. Виховувати інтерес до нових знань, культуру математичних міркувань, навички колективної праці.

Тип уроку: засвоєння нових знань.

Обладнання: портрет Фалеса, опорний конспект «Теорема Фалеса»,  проектор, шматок дошки розміром 60 см х 20 см х 2 см.

Підручник. Бурда М. І. Геометрія: підруч. для 8 кл. загальноосвіт. навч. закл./ М. І. Бурда, Н. А. Тарасенкова. – К.: УОВЦ «Оріон», 2016. – 224 с.

У процесі уроку учні зможуть:                      - ознайомитися з формулюванням  і доведенням теореми Фалеса;                                                                      - застосувати теорему Фалеса під час розв’язування задач прикладного змісту;                                          - виконати експериментальне завдання по знаходженню залежності між відрізками на сторонах кута;                                                                                                                                                                                      - робити логічні висновки, аналізувати поданий матеріал;                                                                                    - поглибити свої знання з історії геометрії;                                                                                                                - удосконалити вміння ділити відрізок на рівні частини.

Попередня робота.          1. Підготувати повідомлення про біографію Фалеса.                                                                                                  2. Підбір рисунків для демонстрації через проектор.

Епіграф уроку. Від часів греків говорити «математика» - означає говорити «доведення». А початок цьому поклав Фалес.                                                                                                                Є. Куртіус.

    Хід уроку.

І. Психолого - організаційний етап.                      Сьогодні чудовий день! І хоч  на нас чекає багато серйозної пізнавальної роботи, хай це не заважає нам залишатися в гарному настрої.                                                                                                                              Рефлексуйте свій робочий настрій на полях робочого зошита:                                                                      ■ – гарно почуваюся;                                                                                                                                                           □ – не добре себе почуваю;                                                                                                                                            ⃝ - не хочу працювати.

ІІ. Виконання експериментального  завдання.                    Учні працюють у парах.                                                                                                                                            Завдання: знайти залежність між відрізками на сторонах кута.                                                                      Обладнання: лінійка, олівець, циркуль.                                                                                                                Алгоритм експерименту:                                                                                                                                            а) накреслити кут;                                                                                                                                                          б) на одній із сторін кута відкласти п’ять рівних відрізків, починаючи від вершини кута;                            в) через отримані точки поділу провести п’ять паралельних прямих;                                                        г) виміряти та порівняти довжини відрізків, отриманих  на другій стороні кута;                                          д) зробити висновок.                                                                                                                                                          Очікуваний висновок: вимірювання показує, що їх довжини рівні між собою.                                          Чи випадково це? Виявляється, що ні! Справедлива так звана теорема Фалеса.

ІІІ. Вивчення нового матеріалу.                      Отож запишіть тему уроку «Теорема Фалеса». Ви зараз будете працювати у групах і самостійно опрацюєте доведення цієї теореми за опорним конспектом та карткою – інструкцією.                            Зміст картки – інструкції.                                                                                                                                            1. Прочитати формулювання теореми Фалеса у підручнику на стор. 38.                                                        2. На аркуші з опорним конспектом записати , що дано і що довести.                                                        3. Користуючись опорним конспектом, проаналізувати доведення теореми.                                          4. Дати відповіді на запитання.                                                                                                                              - Назвати теореми , на які спирались у ході доведення теореми  Фалеса.                                                        - За яких умов В₁В₂=В₂В₁? (Якщо ці відрізки будуть сторонами рівних трикутників).                                          - За яких умов ∆В₂В₁F=∆В₂В₃Е? (За стороною і двома прилеглими до неї кутами).                                          - За яких умов прилеглі кути до сторін FВ₂, В₂Е будуть рівними? (Як різносторонні при паралельних прямих і як вертикальні).                                                                                                                              5. Виконання завдання.                                                                                                                                            6. Звіт про виконання завдання у кожній групі.

ІІІ. Формування вмінь і навичок застосування теореми Фалеса.                   1. Обгрунтувати  виконання експериментального завдання (виконаного на початку уроку) за теоремою Фалеса.                                                                                                                                                                        2. Розв’язування задач із підручника.                                                                                                                                            № 257, 259 (усно).                                                                                                                                                          №261 із коментуванням.                                                                                                                              3. Поділ довільного відрізка на певну кількість рівних частин (індивідуальне виконання).                                          №265.                                                                                                                                                                        4. Будь-яка теорія цінна для практики.                                                                                                                              А). Практична робота: треба розрізати дошку по ширині на 5 рівних частин (рейок). Чи можна зробити розмітку (рис. 1), не вимірюючи ширини дошки? (Рисунок демонструється через проектор). 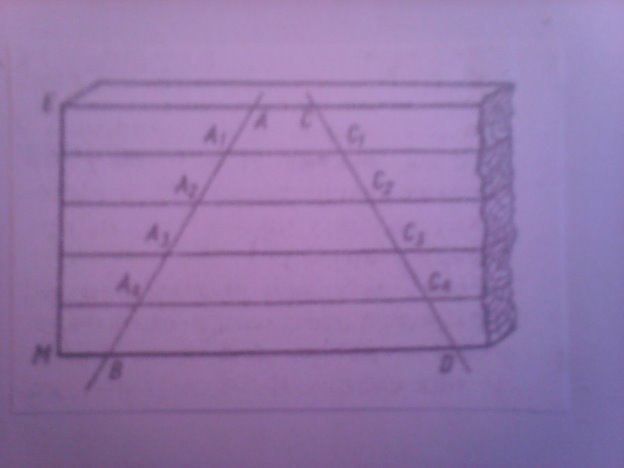                                                                                                                                                                                                                                                                          Рис.1.                                                                                                                                                                                                                                                                                                                    Після деяких роздумів учнів, вчитель зауважує, що для поділу дошки на n частин, столяр прикладає вимірювальну лінійку так, щоб довжина відрізків АВ і СД   (рис. 1) виражалася цілим числом, котре ділиться на 5 без остачі (це полегшує виконання практичного завдання). Точки поділу відрізків АВ і СД сполучає прямими лініями.                                                                                                                Завдання: довести, що довжина відрізка МЕ (ширина дошки) також поділиться на 5 рівних частин.                                                                                                                                                                                                    Б). Самостійно зробити розмітку на дошці, користуючись таким способом (робота у парах).

ІV. Історична довідка.                         Розповідь учня, який заздалегідь підготовив повідомлення про Фалеса.                                                        Фалес  Мілетський (640-548 рр. до н.е.) – давньо - грецький філософ, математик, астроном, купець, політичний діяч,…  З його ім’ям пов’язують  початок розвитку в Греції геометрії як науки.  Фалес розвинув і поглибив багато тверджень про трикутники і лінії взагалі. У Фалеса вперше в історії математики зустрічаються доведення теорем. Якщо єгипетських землемірів задовольняла відповідь на питання «Як?», то Фалес , мабуть першим у світі задав питання «Чому?» і успішно відповів на нього. Фалесу приписують відкриття і доведення ряду теорем: про поділ кола діаметром навпіл; про те, що кут, вписаний у півколо є прямим; про рівність кутів при основі рівнобедреного трикутника; про рівність вертикальних кутів; про пропорційність відрізків, утворених на прямих, що перетинаються декількома паралельними прямими. Фалес установив, що трикутник повністю визначається стороною і прилеглими до неї кутами. Як вважають історики, саме Фалес увів у застосування як основні геометричні інструменти циркуль і лінійку.                                           Твори Фалеса до нас не дійшли (за переказами вони складаються з двохсот віршів).                            Як інженер, Фалес прославився будівництвом стратегічної греблі. Яка змінила напрям течії річки,               внаслідок чого утворився брід, через який рушило військо Креза. Тоді греблю було відкрито і води річки знищили цю армію.                                                                                                                              Фалеса з Мілету у 582 році було проголошено одним з семи мудреців світу.                                          Розповідають , що Фалес раптово помер у похилому віці під час олімпійських ігор.                                          Історики стверджують, що на його гробниці було викарбовано напис «Наскільки малм ця гробниця, настільки велика слава цього царя астрономів у світі зірок».

V. Підбиття підсумків і самооцінка учнями результатів уроку.                     Учням ставиться запитання з використанням вправи «Мікроон».                                                                      1. Що нового ви дізналися на уроці?                                                                                                                              2. Над виробленням яких навичок і вмінь працювали?                                                                                    3. Що сподобалось під час уроку, а що ні?                                                                                                                4. Як ви оцінюєте свою особисту працю на уроці?                                                                                                  5. Чи з’ясували для себе,  що із вивченого потребує доопрацювання?                                                       

VІ. Повідомлення домашнього завдання.                      Вивчити $6, №264, 263.

Використана література.                        1. Погорєлов О. В. Геометрія: Планіметрія: Підруч. для 7-9 кл. серед. шк.. – К.: Освіта, 2000.              2. Возняк Г. Прикладні задачі: від теорії до практики./ Г. Возняк, О. Возняк. – Тернопіль: Мандрівець, 2003.                                                                                                                                                                        3. Возняк Г. Уроки геометрії у 8 класі./ Г. Возняк, Г. Гап’юк. – Тернопіль: Підручники і посібники, 2004.                                                                                                                                                                        4. Савченко Л. В. Опорні конспекти. Геометрія. 8-й клас. Математика, № 187-188, 2002.                            5. Шмигевський М. В. Видатні математики. Харків: Основа, 2004.