Урок. "Теорема Піфагора та її застосування"

         Тема уроку: Теорема Піфагора

 Мета уроку: Повторити з учнями зміст і доведенням теореми Піфагора та наслідків з неї; показати застосування теореми при розв’язуванні задач. Розвивати логічне мислення школярів, формувати навики самооцінки, виховувати інтерес до історії математики.

 Обладнання уроку: Комп’ютер, дошка, портрет Піфагора, плакати з усними вправами, малюнки до задач, картки для практичних робіт, математичне лото.

 Тип уроку: урок узагальнення та систематизації  знань та умінь.

 Очікувані результати:

 засвоєння учнями теореми Піфагора і наслідки з неї;

 вироблені уміння розв’язувати найпростіші задачі з теми;

 викликаний інтерес до біографії Піфагора як легенди і джерела дискусії;

 вдосконалені навики роботи на комп’ютері, застосування їх для здобуття нових знань;

 навчання учнями робити власні висновки.

 

План уроку

І. Організаційний момент.

Вчитель: Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання і нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір. Я надіюся на нашу співпрацю, свідоме засвоєння матеріалу уроку, зацікавленість до продовження роботи над мультимедійним проектом. Запишіть, будь-ласка, число, класна робота і свої очікування від уроку.

 У кулачному бою на  58-й Олімпіаді, яка проходила в 548 році до н.е. брав участь один із давньогрецьких математиків. Переказують, що через малий зріст судді не хотіли допустити його до змагань.

 - Можливо, - заперечив молодий вчений, - мій вигляд і не викликає у вас довіри. Але я буду наносити удари з такою математичною точністю, що супротивникові стане жарко. Моя глибока віра в число – це моє життєве кредо.

 І він додержав свого слова – став чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах.

 То ж нехай його слова: „ Тимчасова невдача краща від тимчасової удачі” стануть девізом уроку.

 

 ІІ. Актуалізація опорних знань та умінь.

 

 

1. Вправа „ Снігова лавина ”:

• Катет, прямокутний трикутник, єгипетський прямокутний трикутник, ….
• Трикутник, прямий кут, прямокутний трикутник,……….

 

2. Усні вправи за плакатами: (слайд 4,5)

 

 ІІІ. Повідомлення теми, мети уроку, мотивація навчальної діяльності.

 

 ІV. Повторення вивченого матеріалу.

1. Математичне лото. (слайд 6, 7)

 

Вчитель. А чи потрібна теорема Піфагора в житті? Побачимо. (слайд 8,9)

 

2. Усне розв’язування задач на знаходження гіпотенузи прямокутного трикутника (використовуються малюнки до задач) – „Займи позицію”.

 

А) Знайдіть довжину приставленої до будинку драбини, якщо нижній кінець знаходиться на відстані 5 м від будинку, а верхній – на стику стіни й даху. Висота стіни будинку дорівнює 12 м.

 Дано: ∆ АВС, С = 90⁰, АС= 5 м, ВС= 12 м

 Знайти: АВ

 Відповідь. 13 м.

 Б) висота новорічної ялинки 9 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ₁, АВ₂ однакової довжини і закріпили їх на підлозі на відстані 12 м від основи ялинки. Якої довжини повинна бути натягнута проволока, щоб ялинка стояла вертикально. ( АВ = )

 

 Вчитель. Теорема – це твердження яке доводять. Виділимо умову і висновок теореми Піфагора.

 

3. Доведення теореми Піфагора  (слайд  10)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V. Формування практичних навичок

1. Розв’язування задач    (слайд 11- 16)    

 

   1. Сторони прямокутного трикутника 5см і 4 см. Знайдіть периметр цього трикутника. ( 2 розв’язки).

 

Відповідь: 5+4+3=12(см). 5+4+ =9+        

 

2. Медіана, проведена до гіпотенузи прямокутного трикутника дорівнює 75 см, а катети відносять ся як 3:4. Знайдіть периметр трикутника.

 

Гіпотенуза 150 см. 150=5х, х=30. Р =150+90+120=360 см.

3. З точки до прямої проведено дві похилі. Довжина однієї з них дорівнює 15 см, а її проекція на цю пряму 12 см. знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.

Відповідь 9 см.

Вправи для зняття втоми очей.

1.Швидко кліпати очима протягом 15 с.

2.Заплющити очі. Не відкриваючи очей, начебто подивитися ліворуч на рахунок „раз-чотири”, повернутися у вихідне положення. Так само подивитися праворуч на рахунок „п’ять-вісім” і повернутися у вихідне положення. Повторити 5 разів.

3.Спокійно посидіти із закритими очима, розслабившись протягом 5 с.

 

4. У прямокутний трикутник  вписано коло. Точка дотику поділяє один з катетів  на відрізки  3 см і 5 см, рахуючи від вершини прямого кута. Знайдіть гіпотенузу і другий катет трикутника.

 

Відповідь  17см і 15 см.

 

5. У трикутнику АВС АВ=ВС=см. Точка перетину медіан віддалена від вершини В на 6 см. Знайдіть медіану трикутника, проведену до бічної сторони.

 

Відповідь Якщо ВО=6 см, то ВД=9 см. Тоді АД=4 см. АО=5 см, АК=7,5 см.

 

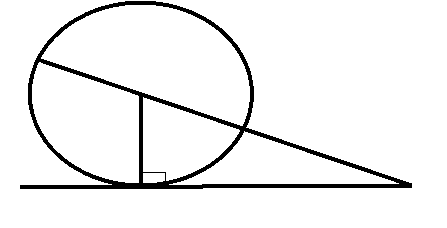
6. З вершини С прямокутного трикутника АВС (∠С=90°) проведено висоту СД та медіану СО (як показано на рисунку). СД=24 см. СО=25 см. Знайдіть периметр трикутника АВС.    

 

 

5.  Історична довідка про Піфагора.

 Учитель.

Піфагор – один із найбільш знаменитих учених за всю історію людства. Він був не лише вченим і засновником першої наукової школи.  Ця унікальна людина була і „володарем душ”, і проповідником власної „піфагорської” етики, і великим філософом. Піфагор виховав у людства віру в могутність розуму, переконаність у можливості пізнання природи, впевненість у тому, що ключем до таємниці світопобудови є математика.

  Учень робить повідомлення про Піфагора.

Вправа „Оціни себе”.

 

 

 

VІ. Домашнє завдання: вивчити п. 63, повт. 62.

 Середній рівень: № 2 (1), 3 (1)

 Достатній рівень: № 2 (2), 3 (3)

 Високий рівень: № 6 (2), № 7 § 7 с. 107.

 Додаткова задача (за бажанням учнів)

 

 

         VІІ. Підсумки уроку.

1. Усна вправа – знайдіть помилку – „Метод ПРЕС”. (слайд 17)

 

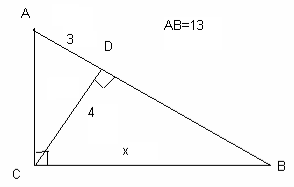
  DВ = 13-3 = 10,

   З ∆ DСВ:  Х² = 4² + 10² = 116

З  ∆ АСД:  ВС² = 16 + 9 = 25

З   ∆ АСВ:  Х² = 169 – 25 = 144

                   116 ≠ 144 

 

 

 

 

 

Вчитель. Історія теореми Піфагора цікава. Адже була відома у Вавілоні ще за 1500 років до народження Піфагора. Можливо, що тоді ще не знали її доведення, а співвідношення між гіпотенузою і катетами було встановлено дослідним шляхом на основі вимірів. Піфагор, очевидно, знайшов доведення цього співвідношення. Збереглася давня легенда, що на честь такого відкриття Піфагор приніс у жертву сто биків, хоча за іншими версіями вчений був непримиренним противником жертвування тварин, особливо великої рогатої худоби.

 В різних джерелах теорему Піфагора називають „теорема нареченої”, „ослиний міст”, „Піфагорові штани”.    

2. Вправа „Мікрофон”.

Що нового  дізнались на уроці?

Як читається теорема Піфагора?

Які наслідки з теореми Піфагора?

Що корисного для себе ви винесли з уроку?

Де, у яких ситуаціях ви можете використати набутий на уроці досвід?

Що було потрібним на уроці? зайвим?

Що ви очікували від уроку? чи збулися ваші очікування?

 

 

 

 

 

 

 

 

 Додаткові завдання та інформація до уроку

 

 На березі річки росла тополя висотою 15м. Буря зламала дерево на висоті 6 м від землі так, що вершина уперлась в інший берег. Знайдіть ширину річки СВ, якщо вважати, що АСВ = 90⁰.

 

 

 

 Вчитель. Математику та літературу іноді ставлять на протилежних полюсах людського знання. Проте мости між літературою й точними науками ніколи не розводилися, адже людський інтерес не можна відділити від емоцій, а „сухі” формули не ізольовані від гарячого „випромінювання” людських почуттів.

 Сонет відомого німецького поета ХІХ століття Адельберта фон Шаміссо є прикладом гармонійного поєднання поезії з геометрією.

 

Як Істину відкрив – сіять їй вічно,

Вона нам – найнадійніша опора:

Так в древній теоремі Піфагора

Й донині бездоганно все й логічно.

 

 

3 м	Квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів
а2 = в с	Так
Відношення прилеглого катета до гіпотенузи	5 м

 

 

У прямокутному трикутнику будь-який з катетів менший за гіпотенузу	1 м
Ні	а с =в а
7 м	Відношення гіпотенузи до прилеглого катета

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тести

 

 1. Як називаються сторони прямокутного трикутника, які утворюють гострий кут?

   а) катети     б) гіпотенуза        в) катет і гіпотенуза  г) два катети і гіпотенуза

 

 2. Знайдіть сторону ромба, якщо його діагоналі дорівнюють 6 см і 8 см.

 

 а) 15 см         б) 10 см         в) 5 см            г) 14 см

         3. Сторони прямокутника 8 см і 15 см. Знайдіть його діагональ.

 

                       а) 23 см         б) 10 см         в) 3 см            г) 17 см

 

 4. Як читається теорема Піфагора?

 а) квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його катетів

 б) квадрат гіпотенузи прямокутного трикутника дорівнює різниці квадратів його катетів

 в) гіпотенуза прямокутного трикутника дорівнює сумі катетів

 г) с² = а² – в²

 

 5. Катети прямокутного трикутника дорівнюють 5 і 12 см. Чому дорівнює гіпотенуза трикутника?

                  а) 15 см         б) 14 см         в) 13 см            г) 16 см

 6. Гіпотенуза прямокутного трикутника дорівнює 10 см, а один з катетів 8 см. Чому дорівнює другий катет?

                  а) 25 см          б) 6 см            в) 5 см             г) 1 см

 7. Порівняйте катети а і в прямокутного трикутника з його гіпотенузою.

 а)  а < c, в > c  б)  a < c, в = c  в)  a > c, в > c  г)  a < c, в < c

 

 8. Катети рівнобедреного прямокутного трикутника дорівнюють 4 см, тоді його гіпотенуза дорівнює

 

                          а) 2 см         б) 4 см         в) 8 см            г) 16 см

          9. Чи буде прямокутним трикутник зі сторонами 9 см, 12 см і 15 см.

                 а)  так          б) ні            в) неможливо визначити