Урок + презентація на тему "Теорема Фалеса". Геометрія 8 клас

Тема уроку: Теорема Фалеса.

Мета уроку: Довести теорему Фалеса, показати практичне застосування до розв’язування вправ. Розвивати графічну культуру, логічне мислення, вміння аргументувати, робити висновки. Здійснювати міжкурсові та міжпредметні зв’язки. Розвивати пізнавальні інтереси учнів, розширювати кругозір.

Виховувати охайність, свідоме ставлення до навчання.

Обладнання: Портрет Фалеса, історична довідка, вислови Фалеса, малюнки до задач, комп’ютерна презентація .

Тип уроку: Урок вивчення нового матеріалу.

                                                Хід уроку

(Слайд 1)

І.Мотивація пізнавальної діяльності учнів (Слайд 2)

 Один із семи мудреців світу.

Багато подорожував , особливо по Єгипту. Вивчав досвід єгипетських математиків.

Він самостійно визначив висоту єгипетських пірамід , чим здивував єгипетського фараона Амазіса.

  Повернувшись на батьківщину , заснував Іонійську школу.(Слайд 3)

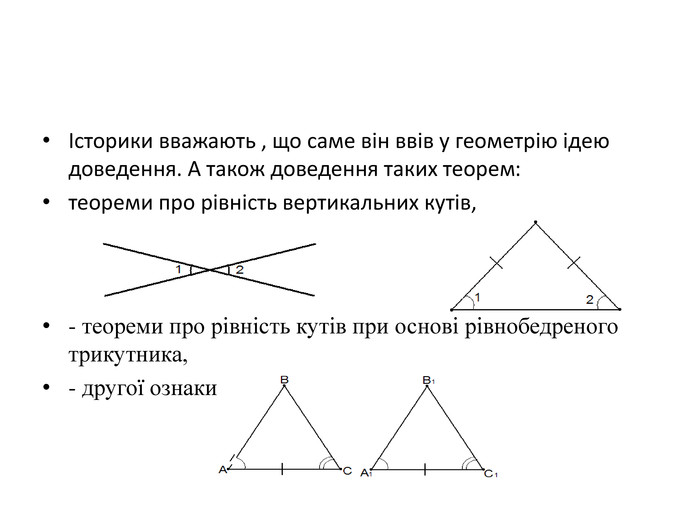
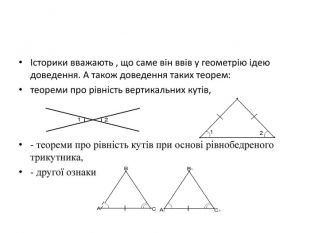
 Історики вважають , що саме він ввів у геометрію ідею доведення. А також доведення таких теорем:

• теореми про рівність вертикальних кутів,

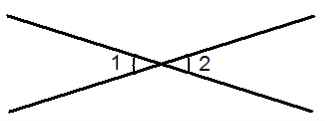
- теореми про рівність кутів при основі рівнобедреного трикутника,

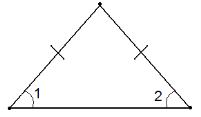
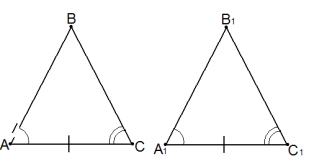-другої ознаки рівності трикутників,

(Слайд 4)

-Кут, що спирається на діаметр , прямий.

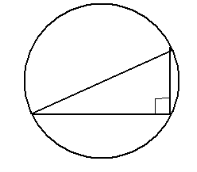
 А також знайшов розв’язання задачі про визначення відстані до корабля, що перебуває в морі.(Слайд 5)

 В астрономії визначив тривалість року 365 днів, довів, що Земля має форму кулі та передбачив сонячне затемнення 28 травня 585 року до нашої ери.

На пам’ятнику йому написано: „Настільки мала ця гробниця, настільки велика слава цього царя в галузі зірок”

 Гадають, що він трагічно загинув на стадіоні великих олімпійських ігор в 80 річному віці. Можливо від спеки, можливо натовп мимоволі заподіяв смерті мудрецеві, а можливо від хвилювання за свого учня  - Піфагора - чемпіона з кулачного бою. .(Слайд 6)

 Ім’я йому – Фалес Мілетський. (портрет)

Це він говорив «Блаженство тіла – в здоров’ї,

блаженство розуму – в знаннях»

ІІ. Повідомлення теми і мети уроку.

Їх в геометрії багато

І всі їх треба добре знати,

Які б ми не вивчали теми

Ми скрізь зустрінемо теореми.

 А от теорема, яку ми сьогодні вивчаємо носить ім’я Фалеса. Він її відкрив і він її довів. Слайд 7

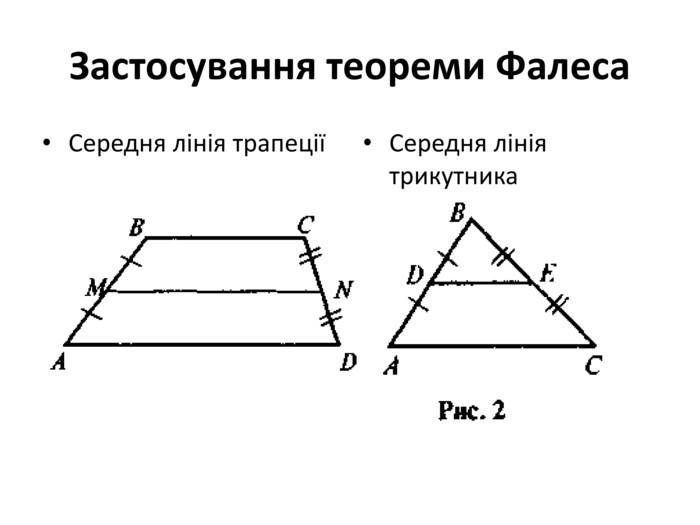
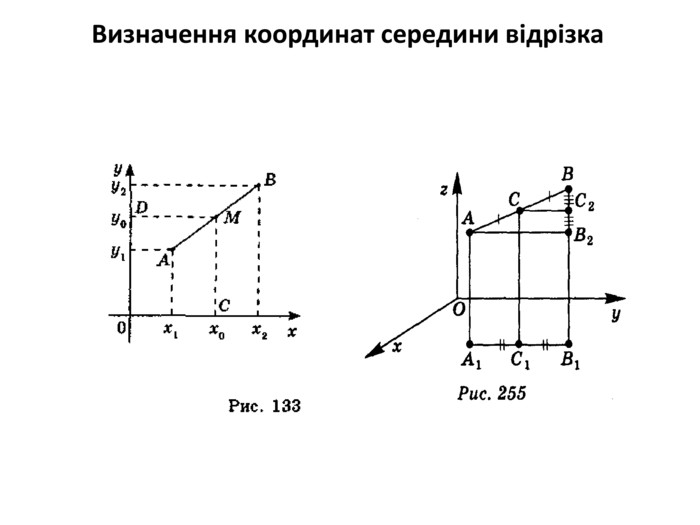
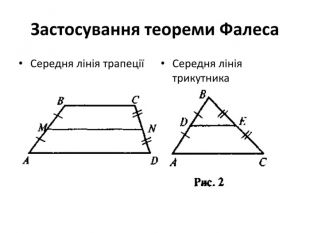
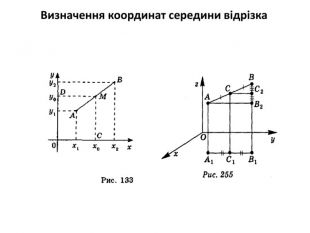
 За допомогою теореми Фалеса можна довести властивість середньої лінії трикутника, трапеції, поділити  за допомогою лінійки і циркуля відрізок на п рівних частин,  Слайд 8 вивести  формули середини відрізка на площині в 8 класі та в просторі в 10 класі . Досить великий клас задач розв’язується за допомогою даної теореми.  Слайд 9

 Але сьогодні буде перший урок вивчення великої за обсягом теми ( 25 годин), яка називається «Подібність трикутників» При її вивченні ми познайомимось із подібними трикутниками та ознаками їх подібності, вивчимо властивість бісектриси кута трикутника, точок перетину медіан та висот трикутника , і , звичайно теорему Фалеса. Записали дату, тему блоку та уроку Слайд 10

ІІІ. Повідомлення девізу уроку.

„Яка радість особливо велика? Коли вдається досягти бажаного.”

Фалес Мілетський. 

 Так бажаним на сьогоднішньому уроці  буде  реалізація трьох задач:

• Відкрити теорему Фалеса.
• Довести її.
• Показати практичне застосування до розв’язування вправ.

ІV. Осмислення та вивчення нового матеріалу.

 1.Практична робота.

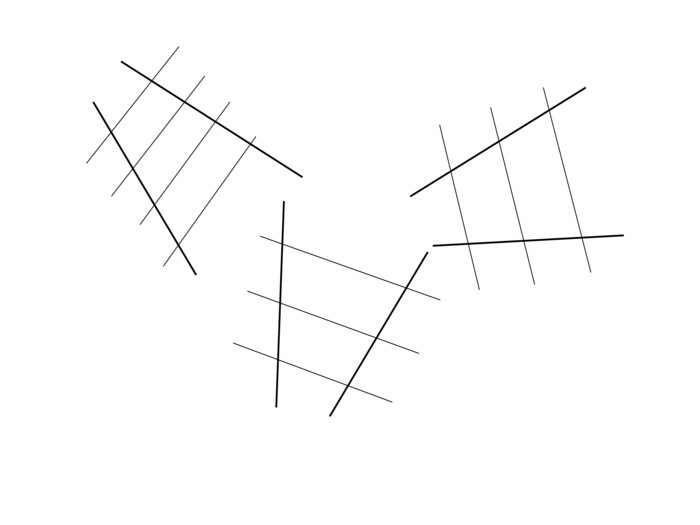
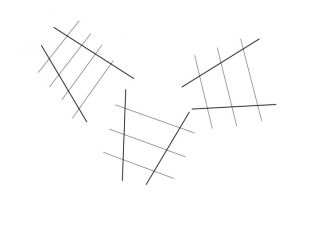
 Накреслити кут. На одній стороні кута відкласти рівні відрізки. Провести паралельні прямі через кінці відрізків. Виміряти та порівняти відрізки, що утворились на другій стороні кута.

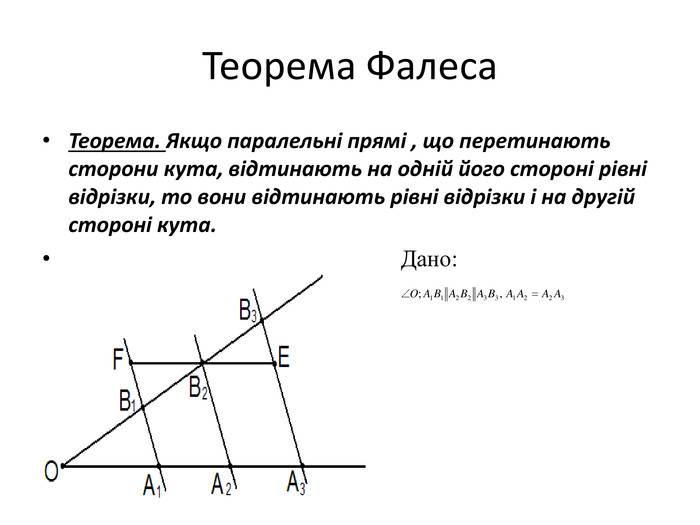
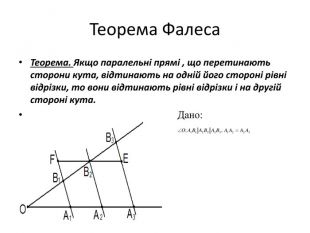
Теорема. Якщо паралельні прямі , що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій стороні кута.                                                             

               Робота з книгою.с.99.

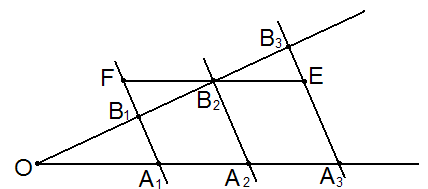Дано:

Довести:                                                                 

                                      Доведення

1.Проведемо Е.

2.- паралелограм.│

    - паралелограм│             Тоді

3.Розглянемо .

  В них : ( за п.2)

               ( як вертикальні)

              ( як внутрішні різносторонні кути при паралельних       прямих ).

За ІІ ознакою рівності трикутників .

4.Звідси .Слайд 11. Ще раз прочитати по слайду теорему

 Зауваження. (Витерти на дошці допоміжну побудову і частину кута до прямих)

 Це буде  теж малюнок до теореми Фалеса. . Слайд 12

У підручнику  подано інше доведення теореми Фалеса. Із яким ви познайомитесь вдома самостійно.

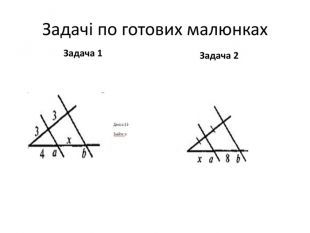
V.Розв’язування вправ. Слайд 13

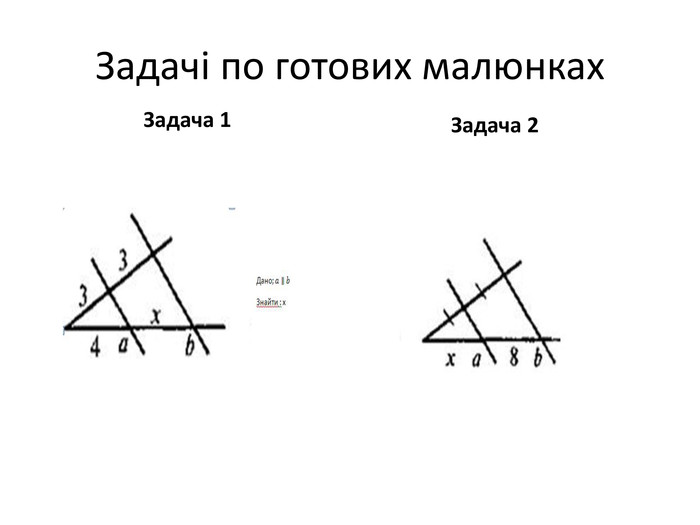
Усні вправи по готових малюнках.

Існує алгоритм доведення вправ за допомогою теореми Фалеса

• 1.Встановити , що на одній стороні кута (прямій ) відкладено рівні відрізки.
• 2.Встановити паралельність прямих, що перетинають дані сторони кута(  дані прямі).
• 3. Зробити висновок.

Слайд 14

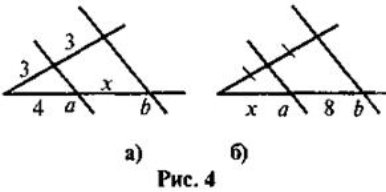
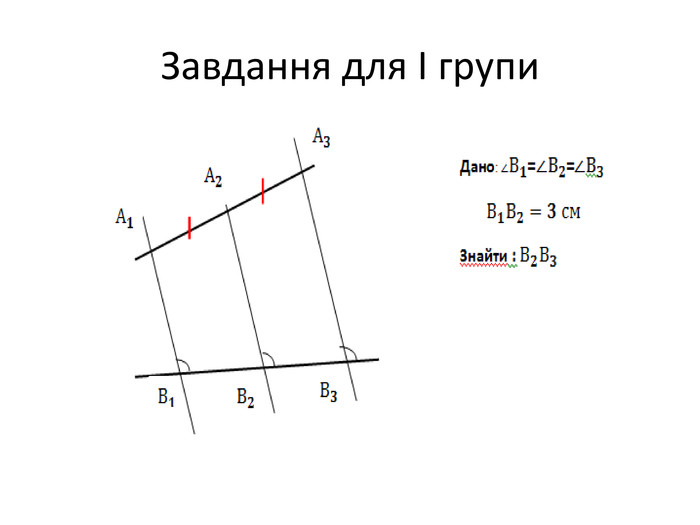
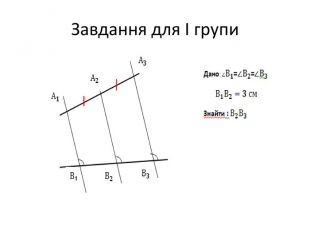
Слайд 15 .Завдання для І групи

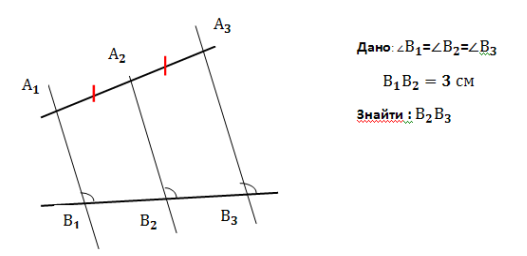
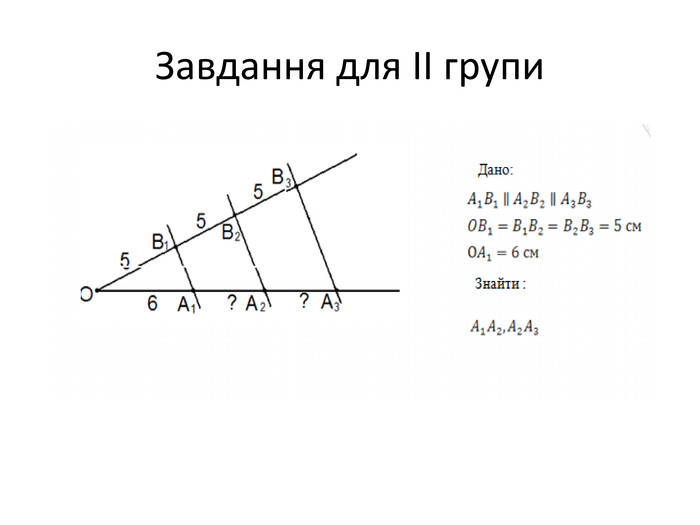
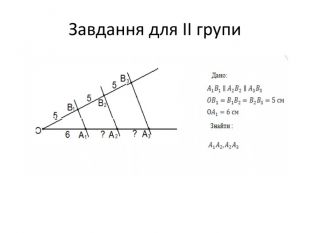
Слайд 16. Завдання для ІІ групи

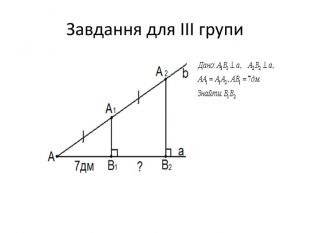
                                                                                       Дано:

  ,

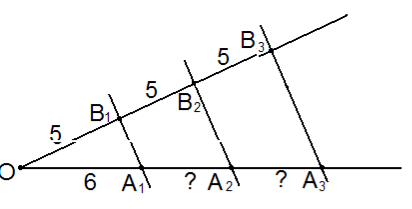
Знайти :
 

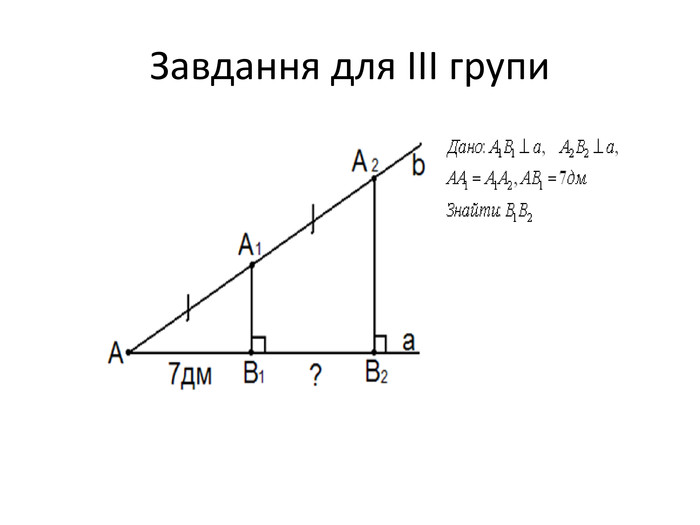
. Слайд 17. Завдання для ІІІ групи

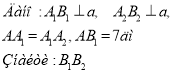
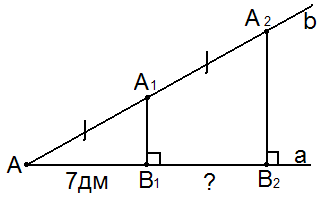
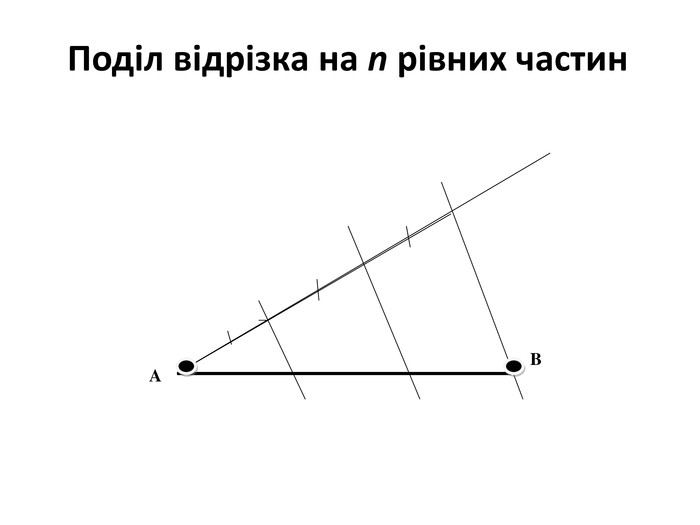
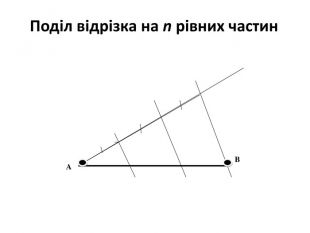
А зараз ми дізнаємось як за допомогою циркуля та лінійки можна поділити відрізок на кулька рівних частин

Слайд 18

    Дано: Відрізок АВ

                                                                                                  Побудувати :

                                                                                                  Поділити на три

                                                                                                  рівні частини

                                   Побудова.

1.Проведимо півпряму а з початком в точці А.

2.Відкладемо на ній три рівні відрізки   .

3.З’єднаємо точку з В.

4.Проведемо прямі .

За теоремою Фалеса

VII.Підсумок уроку.    Підбиття підсумків роботи    учителем.

-Як ви гадаєте чи вдалось нам досягти бажаного?

- Що на уроці було головним? Цікавим?

-  Чого ви навчилися?

- Чим поповнили свої знання?

-   Як працював клас? Окремі  учні?

-  Оцінки тим, хто захищав задачу, хто брав активну участь в обговоренні.

-Чи переконались ви в тому , що Фалес , давньогрецький математик зробив для математики неоціненний вклад? Слайд 19 .А хто пам’ятає речення із якого я розпочала урок ?

VIII. Домашнє завдання. Відшукати  імена ще 6 мудреців світу.

Опрацювати П.15.Вивчити теорему 15.1

Виконати №15.11

  На завершення уроку хочу сказати , що ми з вами наступного уроку глибше дізнаємось про наукову спадщину великого математика, вивчивши узагальнену теорему Фалеса