Розробка уроку на тему " Віднімання натуральних чисел."

Тема. Віднімання натуральних чисел.

Мета: ввести поняття і зміст дії віднімання; сформувати навички віднімання багатоцифрових чисел.

Тип уроку: засвоєння нових знань.

Хід уроку

І. Актуалізація опорних знань

Усні вправи

1. Суму чисел 19 і 8 зменшити на 27.
2. Від числа 53 відніміть суму чисел 13 і 17.
3. Які з наведених записів є записами одного й того ж самого числа?

1) 300 + 40 + 5; 2) 3000 + 400 + 5;  3) 3405;

4) 3 · 1000 + 4 · 100 + 5 · 1;  5) 3045; 6) 345.

II. Засвоєння знань

Задача 1. Група туристів, що складається з 14 осіб, пішла в похід місцями бойової слави. П'ять туристів поїхали автобусом, а решта відпра­вились пішки. Скільки туристів відправилось пішки?

 Аналіз розв'язання

Якщо число туристів, які подорожували пішки, невідоме (позначимо його літерою х), то умову задачі можна записати так: 5 + х = 14.

Тобто в задачі треба за відомою сумою двох чисел (14) і одним відомим доданком (5) знайти невідомий доданок (х), який знаходимо відніман­ням:

х = 14 – 5; х = 9.

Отже, відняти від числа 14 число 5 — означає, що треба знайти таке число х, яке в сумі з числом 5 дає число 14.

Задача 2. На кінець І семестру у 5 класі було 18 учнів, що вчаться на достатньому рівні. Але за II семестр кількість таких учнів збільшилась, і на кінець року таких стало 23 учні. На скільки збільшилась кількість учнів 5 класу, що навчаються на достатньому рівні?

Розв'язання

Якщо шукана кількість учнів невідома (позначимо її літерою х), то умову задачі можна записати так: 18 + х = 23. Отже, знову в задачі знаходи­мо невідомий доданок (х) за відомою сумою (23) і другим відомим додан­ком (18). Зрозуміло, що х = 23 – 18; х = 5 і відняти від 23 число 18 — означає, що треба знайти таке х, яке б у сумі з числом 18 дало число 23.

Після цих пояснень навіть учні можуть сформулювати означення:

Відняти від числа а число b — означає знайти таке число х, яке б у сумі з b давало число а:

a – b = x, х + b = а.

При цьому а — зменшуване; b — від'ємник; а – b, х — різниця.

Зауваження. З означення віднімання випливає, що правильність від­німання перевіряється додаванням (до різниці додати від'ємник, щоб от­римати зменшуване).

Приклад

Що означає відняти: 1) від 18 число 9; 2) число 7 від 12?

Як перевірити правильність виконання дії віднімання?

Задача 3

1) На скільки число 62 більше від 38?

2) На скільки 49 менше за 81?

    Щоб відповісти на запитання, треба відняти:

1) 62 – 38 = 24; 2) 81 – 49 = 32

Отже, різниця а і b показує, на скільки а більше від b, або на скільки b менше від а.

Задача 4. На яке число треба зменшити число 24; 38; 1; 0, щоб отримати

1) нуль; 2) ці самі числа

Розв'язання. З властивостей додавання відомо, що а + 0= а, отже, за оз­наченням віднімання, 0 = а – а, а = а – 0, тобто:

1) 24 – 24 = 0; 38 – 38 = 0; 1 – 1 = 0; 0 – 0 = 0;

2) 24 – 0 = 24; 38 – 0 = 38; 1 – 0 = 1; 0 – 0 = 0.

Завдання 5. Як додати 23 795 до 7 459? Як знайти різницю цих чисел?

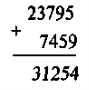
Отже, віднімання виконується теж «у стовпчик». Правильність вико­нання можна перевіряти додаванням:

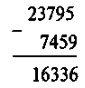
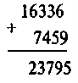
III. Закріплення знань. Формування вмінь

Усні вправи

1. Що означає відняти:

1) від 48 число 12; 2) 17 від 32; 3) від суми 13 і 5 число 7; 4) від т число п?

2. Назвіть компонент дії в кожній рівності. Як перевірити правильність
   віднімання?

12 + 19 = 21; 19 – 12 = 7; 48 – 11 = 38; 45 + 11 = 56.

3. Яке число стоїть в кінці ланцюжка обчислень?

Вправи для письмового розв'язання

№ 211 (1, 2, 4); 213; 215; 234 (1, 3, 5, 6); 238 (1).

 Вправи № 211, 213, 215 — обов'язкового рівня, призначені для форму­вання вмінь виконувати віднімання багатоцифрових чисел.

 Вправу № 234 можна дати на цьому уроці як логічне продовження теми віднімання багатоцифрових чисел з попереднім представленням величин через одну одиницю вимірювання.

Наприклад

76 м 39 см – 41 м 24 см = 7639 см – 4124 см = 3515 см = 35 м 15 см

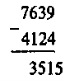
 Вправа № 238 (1) пропонується сильним учням, які добре засвоїли правила віднімання багатоцифрових чисел у початковій школі, а також матеріал теми «Натуральні числа» в 5 класі.

IV. Домашнє завдання

п. 8; усно: №№ 209, 210; письмово: №№ 212 (1-3); 214; 218; 235 (1,3).