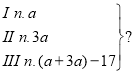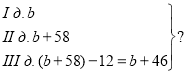Розробка уроку на тему "Вирази. Тотожності"

Варіант 1

Варіант 2

№ 1. Спростіть вираз:

4(5а – 3b) – (-b + 2а).

№ 1. Спростіть вираз

3(4х – 2z) – (5z + 10х).

№ 2. Знайдіть значення виразу:

4 : (-0,8) – .

№ 2. Знайдіть значення виразу

0,35 · – .

№ 3. Доведіть тотожність:

7(4 – a) – 3(-3а + 1) – 25 = 2а.

№ 3. Доведіть тотожність

9,8b = 5 + 9b – 1,2b – 2(2,5 – b).

№ 4. При яких значеннях змінної має зміст вираз ?

№ 4. При яких значеннях змінної має зміст вираз ?

№ 5. Спростіть вираз і знайдіть його значення:

0,5(1,6х – 6,4у) – 2,4(1,5х + у),

якщо х = 3, у = -4,5.

№ 5. Спростіть вираз і знайдіть його значення:

1,5(-2,4а + 3,8b) – 1,6(2,5а – b),

якщо а = 2; b = -3.

№ 6. На першій полиці стоїть а кни­жок, на другій — утричі більше, ніж на першій, а на третій — на 17 книжок менше, ніж на першій і другій полицях разом. Запишіть у вигляді виразу кількість книжок на трьох полицях ра­зом. Обчисліть при а = 20.

№ 6. За перший день магазин продав b кг цукру, за другий — на 58 кг більше, ніж за перший, а за третій — на 12 кг менше, ніж за другий. Запишіть у вигляді виразу кількість кілограмів цукру, проданого ма­газином за три дні. Обчисліть при b = 45.

№ 7*. Доведіть, що сума тризначного числа і подвоєної суми його цифр ділиться на 3.

№ 7*. Доведіть, що шестицифове число, в запису якого перші три цифри однакові й останні три цифри однакові, ділиться на 37.

Варіант 1

Варіант 2

№1.    4(5а – 3b) – (-b + 2а) =

= 20а – 12b + b – 2а = 18а – 11b.

№1. 3(4х – 2z) – (5z + 10x) =

       = 12x – 6z – 5z – 10x = 2x – 11z.

№2. 4 : (-0,8) – = -5 - = -5.

№2.  0,35 · – =

        = -0,28 – 0,36 = -0,64.

№3. 7(4 – а) – 3(-3а + 1) – 25 =

        = 28 – 7а + 9а – 3 – 25 = 2а.

№3. 5 + 9b – 1,2b – 2(2,5 – b) =

       = 5 + 9b – 1,2b – 5 + 2b = 9,8b.

№ 4. має зміст при всіх а, окрім а = -2,5, бо при а = -2,5  2а + 5 = 0.

№ 4. має зміст при всіх х, окрім х = 2, бо при х = 2   7х – 14 = 0.

№ 5. 0,5(1,6х – 6,4у) – 2,4(1,5х + у) =

      = 0,8х – 3,2y – 3,6х – 2,4y  =

      = -2,8х – 5,6y.

Якщо х = 4, у = -4,5, то

       -2,8х – 5,6у = -2,8 · 3 – 5,6 · (-4,5) =

       = -8,4 + 25,2 = 16,8.

№ 5. 1,5(-2,4а + 3,8b) – 1,6(2,5а – b) =

     = -3,6а – 5,7b – 4а  + 1,6b =

     = -7,6а - 3,9b.

Якщо а = 2, b = -3, то

-7,6а – 3,9b = -7,6 · 2 – 3,9 · (-3) =

= -15,2 + 11,7 = -3,5.

№6. 

а + 3а + ((а + 3а) – 17) =

       = 4а + 4а – 17 = 8а – 17.

Якщо a = 20,

то 8а – 17 = 8 · 20 – 1 7 = 143.

№6.

b + (b + 58) + (b + 46) = 3b + 104.

Якщо b = 45, то 3b + 104 =

= 3 · 45 + 104 = 135 + 104 = 239.

№7. + 2(а + b + с) = 3х, де х —ціле.

+ 2(а + b + с) =

= 100а + 10b + с + 2а + 2b + 2с =

= 102а + 12b + 3с =

= 3 · 34а + 3 · 4b + 3с = 3(34а + 4b + с)

- ціле, натуральне. Отже,

+ 2(a + b + с) ділиться на 3.

№7. = 37 · х,

      де х —ціле (натуральне).

= 100000a + 10000a + 1000a + +100b + 10b + b = 111000а + 111b =

= 111(1000a + b) = 37 · 3 · (1000а + b) — натуральне, бо а, b — цифри, тому ділиться на 37.