Презентація до уроку " Розв'язування найпростіших тригонометричних нерівностей"
Про матеріал
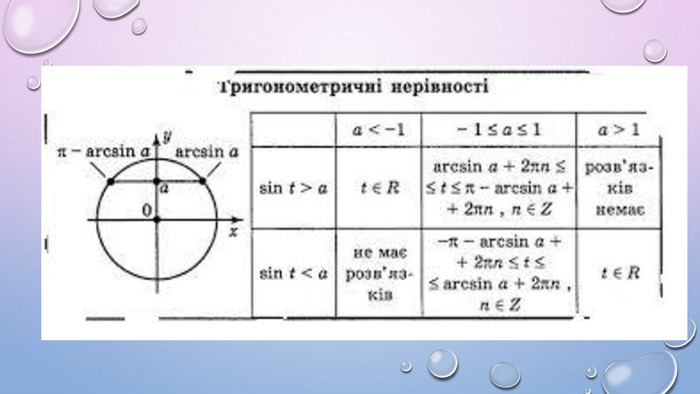
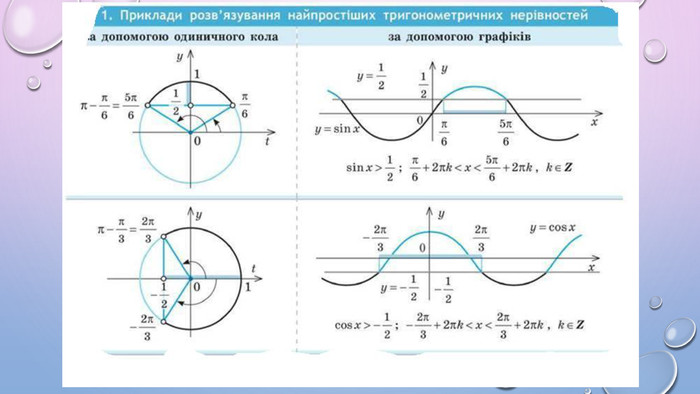
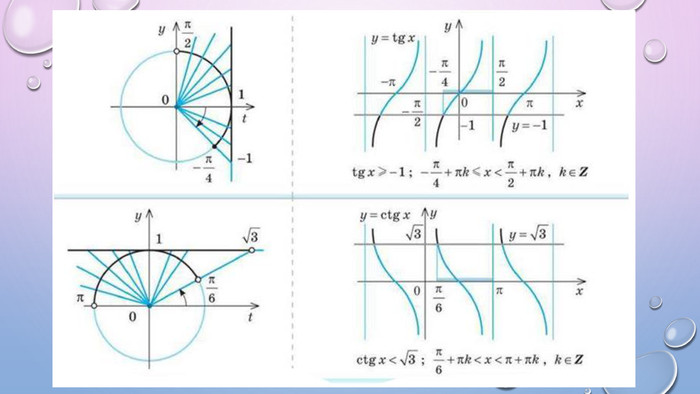
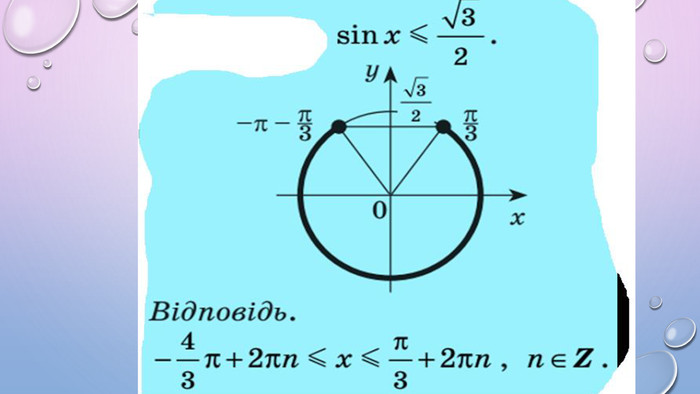
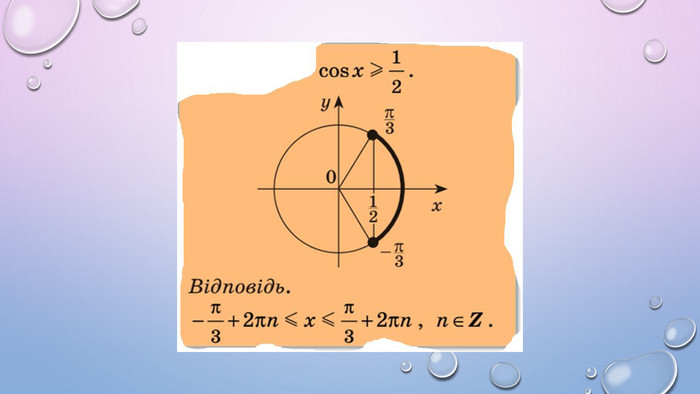
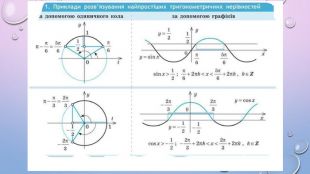
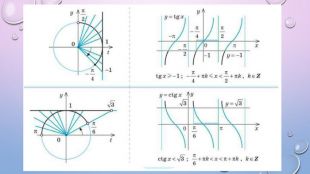
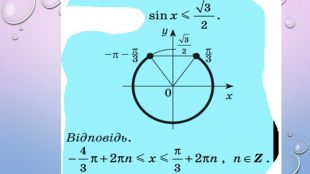
Презентація містить теоретичний матеріал у вигляді таблиць, які допомагатимуть учням під час розв'язування нерівностей. А також приклади розв'язаних нерівностей за допомогою одиничного кола Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку