Тема. Математичний маятник. Формула періоду коливань математичного маятника. Розв’язування задач Мета:

− формувати поняття математичного маятника, вивчити залежність періоду коливань математичного маятника від його довжини та прискорення вільного падіння, формувати вміння застосовувати отриманні знання при розв’язуванні задач на рух математичного маятника, розширювати та поглиблювати знання про коливальні рухи та їх характеристики;

− розвивати уміння здобувати міцні і свідомі знання шляхом реалізації практичної діяльності, створювати умови для активної пізнавальної

діяльності;

− виховувати творчу особистість, забезпечувати умови реалізації індивідуальних здібностей.

− використання практичної діяльності студентів для реалізації частковопошукового методу навчання.

Тип уроку: засвоєння нових знань з елементами пошукових досліджень Обладнання: штатив, нитка, набір тягарців, лінійка.

Забезпечення уроку: підручник, збірник задач, картки індивідуального оцінювання, роздатковий матеріал, відео фрагменти, презентація.

Хід заняття:

                 I.     Організація учнів до уроку

Привітання. Облік відвідування. Налаштування на роботу. 

Протягом заняття ви зможете оцінювати самостійно якість своєї праці на занятті. Для цього скористаємося таблицею індивідуального оцінювання (СЛАЙД 2)

 

              II.     Актуалізація опорних знань і чуттєвого досвіду

 

Ми продовжимо працювати над розділом. Вивчення якого розпочали на попередньому занятті. Нагадайте його назву.

Для налаштування на роботу проведемо розумову розминку.

 

Тестування із самоперевіркою (запитання і відповіді у презентації, оцінювання у картці)

(СЛАЙДИ 4-11, 3)

1.     Рухи, при здійсненні яких через рівні проміжки часу координати тіла, швидкість і прискорення періодично повторюються, називаються…

a)     Рухами по колу;

b)    Механічними коливаннями;

c)     Вільними коливаннями.

2.     Серед коливань виберіть вільні:

a)     Рух маятника у годиннику;

b)    Рух шальок терезів;

c)     Рух гойдалки при постійному розгойдуванні.

3.     Гармонічні коливання описують рівнянням:

a)     𝑣 = 𝐴 cos 𝜔𝑡;

b)    𝑥 = 𝜔 cos 𝐴𝑡;

c)     𝑥 = 𝐴 sin 𝜔𝑡.

4.     Час, протягом якого здійснюється одне повне коливання, називається… a) Періодом;

b)    Частотою;

c)     Циклічною частотою.

5.     Частота коливань обчислюється за формулою:

a)     𝜈 = ^𝑛;

𝑡

b)    𝜈 = ^𝑡;

𝑛

c)     𝜈 = 2𝜋𝜔.

6.     Амплітуда коливань вимірюється у

a)     с;

b)    Гц;

c)     м.

7.     Циклічна частота – це величина, яка визначає…

a)     Кількість коливань за 1 с;

b)    Кількість коливань за період;

c)     Кількість коливань за 2𝜋 с.

8.     Чим більша частота коливань, тим їх період…

a)     Більше;

b)    Менше;

c)     Не залежить від частоти.

 

Перевірка відповідей. Оцінювання в таблиці (0,5 б за кожну правильну відповідь) Продовжуйте працювати протягом заняття і накопичуйте бали.

 

            III.       Повідомлення теми і завдань уроку. Мотивація навчальної діяльності

Отже, одним з досить  розповсюджених видів нерівномірного руху є коливальний рух. Він часто зустрічається як в природі, так і в техніці. (СЛАЙД 23-24)

Чим схожі всі ці рухи? (наближено повторюються через певний період часу, характеризуються одними і тими ж величинами)

Для спрощеного вивчення коливальних рухів використовують ідеальну модель коливальної системи – математичний маятник. Він дозволяє дослідити основні властивості і закономірності коливальних рухів, які потім можна застосувати до більш складних коливальних систем.

Тема: «Математичний маятник. Формула періоду коливань математичного маятника. Розв’язування задач» (СЛАЙД 26)

 

            IV.     Сприймання і усвідомлення нового матеріалу

 

Маятник – це фізичний пристрій, який здійснює коливальні рухи.

Як по-іншому можна назвати маятник? (коливальна система)

 

Види маятників: фізичний, математичний, пружинний (демонструю).

 

Математичний маятник – це ідеальна коливальна система без тертя, що складається із невагомої й нерозтяжної нитки, на якій підвішена матеріальна точка.

(ДЕМОНСТРУЮ МОДЕЛЬ МАТЕМАТИЧНОГО МАЯТНИКА)

 

-        Як розпочати коливання маятника? (вивести із положення рівноваги)

-        Куди рухатиметься кулька, якщо її відпустити? (до положення рівноваги)

 

ВІДЕО (1 причини руху маятника)

-        Чому маятник рухається до положення рівноваги? (На нього діє рівнодійна сил тяжіння і натягу нитки, направлена до положення рівноваги)

-        Чи зупиняється маятник у положенні рівноваги? (Ні)

ВІДЕО (2 перетворення енергії)

Висновок: під час коливань маятника відбуваються взаємні перетворення потенціальної і кінетичної енергій.

 

Коливальний рух маятника характеризується періодом коливань. Ми з вами спробуємо самостійно з’ясувати, від чого залежить період коливань математичного маятника.

(УЧНІ ВИСЛОВЛЮЮТЬ ПРИПУЩЕННЯ)

Основні гіпотези:

− Від довжини маятника (І ряд);

− Від маси маятника (ІІ ряд);

− Від амплітуди коливань (ІІІ ряд).

 

(УЧНІ ПЕРЕВІРЯЮТЬ СВОЇ ПРИПУЩЕННЯ ПРАКТИЧНО)

 

Отже, період коливань математичного маятника залежить від його довжини і не залежить від маси та амплітуди коливань.

ВІДЕО (3 підтвердження гіпотез)

Незалежність періоду коливань від маси маятника з’ясував Галілео Галілей.

(ПОВІДОМЛЕННЯ ПРО ГАЛІЛЕЯ)

 

Але період коливань математичного маятника залежить не тільки від його довжини. Однією із сил, яка змушує рухатися маятник. Є сила тяжіння. Вона залежить від прискорення вільного падіння. Що ви знаєте про цю фізичну величину?

Хоч ми і звикли вважати її сталою, насправді ми користуємося стандартним значенням, прийнятим рішенням третьої Генеральної конференції з мір та ваг.

Насправді ж, прискорення вільного падіння набуває різних значень. В залежності від деяких факторів.

(ПОВІДОМЛЕННЯ ПРО ПРИСКОРЕННЯ ВІЛЬНОГО ПАДІННЯ)

 

Маятник коливається з різним періодом у різних точках Землі. Це використовують для відшукання покладів корисних копалин (важких-металів або легких-газів, нафти).

 

Отже, період коливань математичного маятника можна обчислити за формулою

𝑻 = 𝟐𝝅

Ця формула носить ім’я Христіана Гюйгенса. (СЛАЙД)

Треба розуміти, що до фактичної появи математичного аналізу і перших спроб вирішення диференціальних рівнянь (Ньютон, Лейбніц) всі розрахунки такого типу були здебільшого геометричними, так що уявна простота виведення формул такого типу є оманливою. І, незважаючи на практично повну відсутність відповідного математичного апарату в його часи, праці Гюйгенса по маятникам є багато в чому вичерпними навіть з сучасної точки зору.

 

При невеликих амплітудах математичний маятник здійснює гармонійні коливання.

ВІДЕО (4 гармонійні коливання)

Отже, коливання математичного маятника можна описувати законами sin або cos.

 

               V.     Осмислення об’єктивних зв’язків і взаємозалежності у матеріалі

(СЛАЙД 29-34 )

Якісні (бліц-опитування):

− Банку з піском підвісили на довгій нитці. У скільки разів зміниться період коливань банки з піском, якщо в результаті висипання піску маса повної банки зменшиться вдвічі? (Не зміниться)

− Куди треба пересунути сочку маятника (тягарець на стрижні), якщо годинник поспішає? (Вниз)

− Космонавт узяв із собою на Місяць маятниковий годинник. Чи йтиме він на Місяці так само, як і на Землі? (Ні, маса Місяця менша Землі)

− Чи зміниться період коливань гойдалки, якщо замість однієї людини на гойдалку сядуть двоє? (Ні)

− Як і чому зміниться період коливань маятника, якщо його перенести із повітря у воду? (Збільшиться)

− Як і чому зміниться період коливань металевої кульки на нитці, якщо під нею розташувати магніт? (Зменшиться)

(ПОВТОРЕННЯ АЛГОРИТМА РОЗВ’ЯЗАННЯ ЗАДАЧ З ФІЗИКИ)

Кількісні:

№ 422 (1 фронтально), с. 64

Дано:         

l=0,141 м     Т        Т  с     

             Т-?, ν-?        𝜈                 𝜈 Гц   

Т

                                          Відповідь: 0,75 с, 1,33 Гц.

 

№ 422 (2-4 по рядах) Відповідь:

2)  2,01 с, 0,498 Гц.

3)  1,72 с, 0,582 Гц. 4) 2,93 с, 0,341 Гц.

Порівняння результатів (залежність періоду і частоти від довжини маятника)

 

№ 425 Дано:

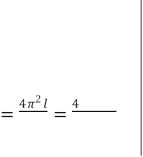
l=80 см    0,8 м     Т = 2𝜋 𝑔  t=1 хв       60 с        n=34                       𝑔          ₂                     ^𝜋2₂^𝑙𝑛2

                                                                           𝑇                  𝑡

g-?                           [g]= ^м₂ Відповідь: 10,13 м/с²

𝑐

 

 

            VI.     Узагальнення і систематизація знань

 

Робота над заповненням таблиці.

Знайома інформація (я це вже знав)
Нова інформація (це для мене нове)
Суперечлива інформація (я думав інакше)
Недостатня інформація (хотілося б дізнатися більше)

 

          VII.     Оцінювання роботи учнів на занятті

Підведення підсумків за карткою

 

       VIII.    Домашнє завдання