Розробка уроку "Пропорція" 6 клас
Розробка уроку з теми «Пропорція» 6 клас.
Тема: Пропорція. Основні властивості пропорції.
Цілі:
навчальна: 1) ввести поняття пропорції; 2) вивести основні властивості; 3) закріпити нові поняття; 4) формувати вміння застосовувати властивості пропорції при вирішенні завдань.
розвиваюча: 1) прищеплювати кожному учневі смак до самостійної, активної творчої діяльності; 2) розвивати пізнавальний інтерес до предмета.
Виховна: 1) виховувати чесність в оцінці своїх знань; 2) навчати працьовитості, акуратності
Тип уроку: творча лабораторія
Методи: дослідження
Обладнання: дошка, підручник, карти настрою, опорні схеми по темі для кожного учня. Комп'ютерна презентація.
Структура уроку.
І. Організаційний етап (5 хв)
ІІ. Пояснення нового матеріалу. (27 хв)
ІІІ. Фізкультхвилинка (3 хв)
ІV. Застосування поняття пропорція в повсякденному житті. ( 5 хв)
V. Підведення підсумків. ( 3 хв)
VІ. Повідомлення домашнього завдання (2 хв)
Хід уроку.
І. Організаційний етап.( 5 хв)
- Перевірка готовності учнів і класу до уроку.
Девіз уроку математики
Міркуємо - швидко!
Відповідаємо - точно!
Лічимо - правильно!
Пишемо - гарно!
- Хтось сьогодні буде задоволений, що зумів вирішити сам або за допомогою однокласників смішне або важке завдання; хтось тим, що він дізнався щось нове; а хтось тим, що йому пощастило, і не довелося думати над завданням.
Перед вами листок настрою

Ви мій настрій бачите, він залежить від вас, від ваших знань. А який ваш настрій? Покажіть його, закрасивши синім олівцем те личко, яке відповідає вашому настрою до початку уроку.
- А тепер розгадайте ребус (картинка на екрані)
![]()
![]()
![]()
![]()

 _ _ _
_ _ _  (пропорція)
(пропорція)
- Отже, ми сьогодні будемо говорити про пропорцію таі її властивості.
- Учитель. Багато чого з математики не залишається в пам’яті, але коли зрозумієш її, тоді легко при нагоді згадати призабуте. (М.В.Остроградський).
Сьогодні в кабінеті математики відкрито науково-дослідницький інститут. Директором НДІ призначили мене, а всі ви - його наукові співробітники. Організовано три лабораторії, в кожній лабораторії я призначаю старшого наукового співробітника. (Видаю таблички «лабораторія №1, №2, № 3» та бейджики «старший науковий співробітник»), вони відповідають за злагоджену роботу всієї лабораторії.
ІІ. Пояснення нового матеріалу (27 хв)
Лабораторія № 1
Відомо, що результат при діленні називається часткою. Проте, нерідко для позначення цього результату використовується слово ... Вирішіть приклади, використовуючи відповіді, дізнайтеся це слово.
2,1 · ![]() = ш
= ш ![]() : 1
: 1![]() = о
= о
3,5 · ![]() = н
= н ![]() = я
= я
4,8 ·![]() = в
= в ![]() : 2 = ц
: 2 = ц
2,4 : ![]() = д 0,5
= д 0,5 ![]()
![]() = р
= р
4![]() : 9 – 4
: 9 – 4 ![]() ·
· ![]() = і
= і 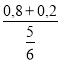 = п
= п
![]() :3 – 0,2 = е
:3 – 0,2 = е ![]()
|
1,8 |
0 |
12 |
1 |
0,5 |
0,7 |
|
1 |
1 |
|
|
в |
і |
д |
н |
о |
ш |
е |
н |
н |
я |
Лабораторія № 2
Вирішіть приклади (ті ж, що і у лабораторії №1), заповніть таблицю і дізнайся, що в математиці, при вирішенні деяких завдань, доводиться мати справу з рівністю двох ...
|
1,8 |
0 |
12 |
1 |
0,5 |
0,7 |
|
1 |
|
|
в |
і |
д |
н |
о |
ш |
е |
н |
ь |
Лабораторія № 3
Дізнайтеся, як називається рівність двох відношень, вирішивши приклади (ті ж, що і у лабораторії № 1), заповнивши таблицю.
|
|
|
|
|
|
|
|
0 |
|
|
п |
р |
о |
п |
о |
р |
ц |
і |
я |
Учитель. Давайте вислухаємо звіти лабораторій про виконану роботу. Зі звітів лабораторій дайте відповідь на питання «що таке пропорція?» (Пропорція - це рівність двох відношень). Вирішимо усно задачу.
Чіп і Дейл купили сир. Чіп заплатив 100 грн. за 2 кг., а Дейл - 150 грн. за 3 кг. того ж сиру. З'ясуйте: «За однакової ціною був куплений сир?»
Учитель записує на дошці:
100 : 2 = 50 (грн.) – чип заплатив за 1 кг.
150 : 3 = 50 (грн.) – Дейл заплатив за 1 кг.
Отримали: 100 : 2 =150 : 3 або запишем по-іншому ![]() =
= ![]() .
.
Ми склали з вами пропорцію.
Запишемо рівність двох відношень в загальному вигляді a : b = с : d ; ![]() =
= ![]()
читається: а, поділене на b, дорівнює с, поділене на d, або відношення а і b дорівнює відношенню с і d, або а відноситься до b як d відноситься до с.
Числа а, в, с, d називають членами пропорції.





 Подивіться на опорну схему яка знаходиться у кожного на столі.
Подивіться на опорну схему яка знаходиться у кожного на столі.


Усно. Назвіть крайні і середні члени пропорції 100 : 2 = 150 : 3.
Учитель. А зараз послухаємо історичну довідку, підготовлену нашим співробітником.
Історична довідка о виникненні пропорції.
Учитель. А зараз проведемо справжню дослідницьку роботу, адже ми НДІ. Лабораторії отримують завдання.
Лабораторія № 1
Дана пропорція 3 : 4 = 9 : 12
1) Поміняйте місцями крайні члени. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію самі. Переконайтеся в цьому ще раз. Зробіть висновок.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Лабораторія № 2
1) Поміняйте місцями середні члени пропорції 3: 4 = 9: 12. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію самі. Переконайтеся в цьому ще раз. Зробіть висновок.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Лабораторія № 3
1) Поміняйте місцями крайні і середні члени пропорції 3: 4 = 9: 12. Чи буде отримана пропорція вірною?
2) Придумайте вірну пропорцію. Переконайтеся в цьому ще раз.
3) Знайдіть добуток крайніх і середніх членів всіх пропорцій. Зробіть висновок.
Учитель. Послухаємо звіт лабораторій про виконану роботу, зробимо висновки. (Заслуховуються звіти кожної лабораторії) Потім вчитель підводить підсумок і формулює властивість пропорції і робить запис на дошці:
ІІІ. Фізкультхвилинка (3 хв)

![]() ІV. Застосування поняття пропорція в повсякденному житті. (5 хв)
ІV. Застосування поняття пропорція в повсякденному житті. (5 хв)
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Архітектура

При побудові храму богині Діани римляни взяли пропорцію, якою відрізняються стрункі жінки: товщина колони складала ![]() її висоти. Тому колони здавалися вищі ніж вони були насправді, як раз за рахунок зменшення товщини. У архітектуру увійшли два види колон, зберігаючи одна чоловічу, друга жіночу пропорцію у відношеннях між основою і висотою.
її висоти. Тому колони здавалися вищі ніж вони були насправді, як раз за рахунок зменшення товщини. У архітектуру увійшли два види колон, зберігаючи одна чоловічу, друга жіночу пропорцію у відношеннях між основою і висотою.
Золотий переріз
«Золотим перерізом» називається поділ відрізка, при якому довжина всього відрізка так відноситься до довжини його більшої частини, як довжина більшої частини до меншої.
![]() Число, рівне відповідним відносинам, називають коефіцієнтом «золотого перетину» і наближене значення цього числа з точністю до десятих часток одно 0,6.
Число, рівне відповідним відносинам, називають коефіцієнтом «золотого перетину» і наближене значення цього числа з точністю до десятих часток одно 0,6.
Вважають, що поняття про золотий поділ ввів у науковий обіг Піфагор, древньогрецький філософ і математик . Є припущення , що Піфагор своє знання золотого поділу запозичив у єгиптян і вавилонян. І дійсно пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту та прикрас з гробниці Тутанхамона свідчать про те, що єгипетські майстри користувались співвідношенням золотого поділу при їх створенні.
У багатьох метеликів співвідношення розмірів грудної та черевної частини тіла відповідає золотої пропорції. Склавши крила, нічний метелик утворює правильний рівносторонній трикутник. Але варто розвести крила, і ви побачите той же принцип членування тіла на 2,3,5,8. Бабка також створена за законами золотої пропорції: відношення довжин хвоста і корпусу дорівнює відношенню загальної довжини до довжини хвоста.

Наш сучасник, американський хірург Стівен Марквардт створив, використовуючи принципи золотого перетину, геометричну маску, яка може служити еталоном прекрасного особи.

Кулінарія.
 Поняття пропорції використовується у кулінарії. Коли ми готуємо яку-небудь страву, ми намагаємось використовувати ту кількість продуктів, яка записана у рецепті, для того щоб страва була смачна. Також пропорція дозволяє розрахувати кількість продуктів для приготування страви для різної кількості людей
Поняття пропорції використовується у кулінарії. Коли ми готуємо яку-небудь страву, ми намагаємось використовувати ту кількість продуктів, яка записана у рецепті, для того щоб страва була смачна. Також пропорція дозволяє розрахувати кількість продуктів для приготування страви для різної кількості людей
Медицина
 В медичній практиці лікарі слідкують за тим, скільки і коли потрібно давати ліки хворому. В правильних дозах ліки дають лікувальний ефект, в менших – вони даремні, в більших – шкодять. При виготовленні лікарських засобів теж дотримуються пропорції.
В медичній практиці лікарі слідкують за тим, скільки і коли потрібно давати ліки хворому. В правильних дозах ліки дають лікувальний ефект, в менших – вони даремні, в більших – шкодять. При виготовленні лікарських засобів теж дотримуються пропорції.
Географія
В географії також застосовують пропорції – масштаб. Масштабом називають відношення довжини відрізку на карті або на плані до довжини відповідного відрізку на місцевості.
V. Підведення підсумків. ( 3 хв)
Робота з картками настрою
Відповідь на питання:
-Я дізнався ….
- Було цікаво….
- Було не зрозуміло …
VІ. Повідомлення домашнього завдання (2 хв)
§ 21, № 531, 539 (1). Творче завдання «Скласти кросворд з понять § 21»


про публікацію авторської розробки
Додати розробку
