Розробка уроку "Розв'язування прямокутних трикутників"

 

Кинашівська ЗОШ І-ІІІ ступенів

Борзнянської міської ради

Чернігівської області

 

 

 

 

 

 

 

 

 

Розв'язування прямокутних трикутників

 

 

Урок геометрії 8 клас

 

                                                    

 

 

 

 

 Підготувала вчитель математики

                                     Кот Людмила Іванівна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема.   Розв'язування прямокутних трикутників

 

Мета: закріпити, систематизувати і перевірити знання з даної теми; повторити означення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника, теорему Піфагора та основні наслідки з неї; закріпити вміння і навички застосувати теоретичний матеріал до розв'язування прямокутних трикутників; показати практично-прикладний характер здобутих знань.

Розвивати міжпредметні зв'язки,  вміння аналізувати, робити висновки, знаходити власні способи розв’язання.

Формувати компетентності: соціальні (розвиток пізнавальної активності учнів, робота в команді, усвідомлення власного внеску в спільну роботу, вміння брати відповідальність), комунікативні (формування власної точки зору, розвиток культури мовлення, вміння доводити власну позицію). Виховувати активність, увагу, кмітливість, самостійність, пізнавальний інтерес до вивчення математики.

Тип уроку: урок застосування   знань, умінь і навичок.

Форма проведення: урок - мандрівка

Обладнання: картки із завданнями, задачі – малюнки, таблиці-вислови, комп’ютер, презентація, портрети вчених, практичні задачі в малюнках.

 

Епіграф:

«Серед рівних розумом – за однакових інших умов – переважає той, хто знає геометрію».                                                           Блез Паскаль

 

Хід уроку

І. Організаційний етап.

 

ІІ. Мотивація навчальної діяльності.

На попередніх уроках ми розглянули прямокутний трикутник, теорему

Піфагора та наслідки з неї, розглянули основні типи задач на обчислення елементів прямокутного трикутника. Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство дізналось ще в давнину. Задачі про трикутники знаходяться у давньоєгипетських папірусах, старинних індійських книгах.

Чому ж трикутник цікавив людей з давніх часів? Жорсткість трикутника використовували під час будівництва й конструювання. Сьогодні наша мета – узагальнити і систематизувати набуті знання з теми «Розв’язування прямокутних трикутників» та показати їх практичне застосування.

Для чого ми вивчаємо тему «Прямокутні трикутники» ?

Чи потрібні нас ці знання в повсякденному житті ? (Обговорення з учнями).

 

 

 

Якщо хочеш досягнути

У житті своїх вершин,

Математику збагнути

Маєш тонко до глибин.

 

 

III. Актуалізація опорних знань.

 

1. Вправа «Продовж речення» - «Мікрофон»

(повторення відомостей про прямокутний трикутник)

• Прямокутним трикутником називається трикутник, який …..
• Сторона прямокутного трикутника, яка лежить проти прямого кута ….
• Сторони прямокутного трикутника, які утворюють прямий кут  …
• Сума всіх кутів трикутника дорівнює…..
• Сума гострих кутів прямокутного трикутника дорівнює …
• У прямокутному трикутнику не може бути …. кута.
• Якщо один із гострих кутів прямокутного трикутника дорівнює 40º, то інший..
• Якщо в прямокутному трикутнику є гострий кут, який дорівнює 30°, то ….
• Прямокутний трикутник з рівними катетами …
• Гострі кути прямокутного, рівнобедреного трикутника …
• Якщо відомі катети прямокутного трикутника, то його площа дорівнює …
• Наприклад, катети прямокутного трикутника дорівнюють 6 см і 8 см, тоді його площа дорівнює …
• Висота прямокутного трикутника, проведена до гіпотенузи є середнім пропорційним між проекціями ….
• Катет  прямокутного трикутника є середнім пропорційним між гіпотенузою і ..
• Відношення протилежного катета до гіпотенузи називається…….
• Відношення протилежного катета до прилеглого називається……
• Відношення прилеглого катета до гіпотенузи називається…..
•  Що більше - похила чи її проекція?
• Як за двома сторонами прямокутного трикутника знайти його гострі кути?

 

2. Завдання за готовими динамічними моделями в програмі GeoGebra.

 

 

 

 

 

 

 

 

 

Завдання 1.

 

 

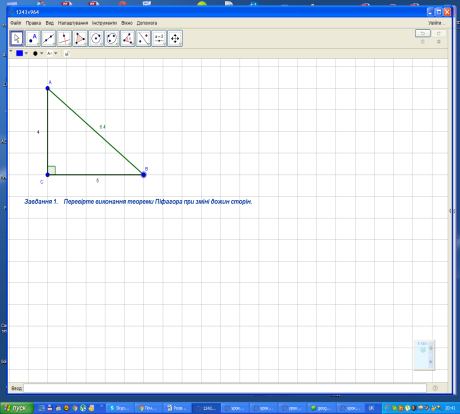
Завдання 2.

 

                                                     

 

 

 

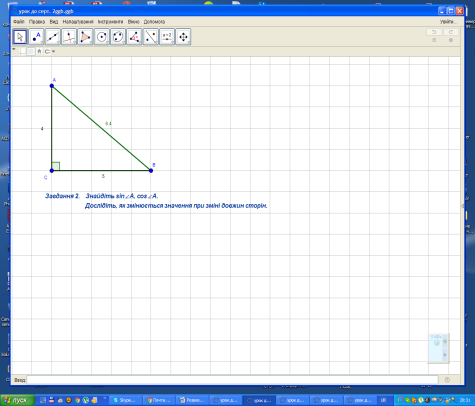
Завдання 3.

 

 

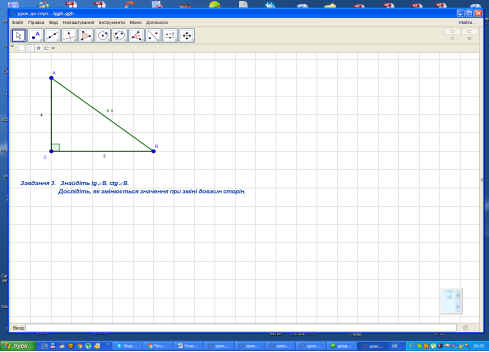
Завдання 4.

 

 

 

 

 

 

 

 

 

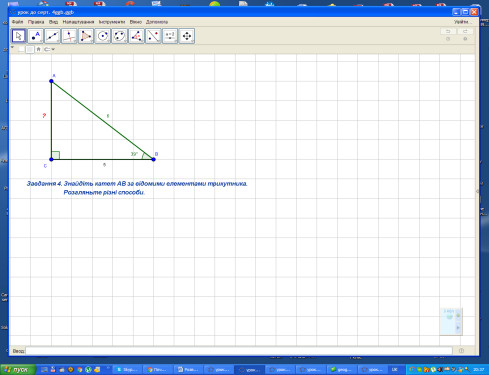
Завдання 5.

 

 

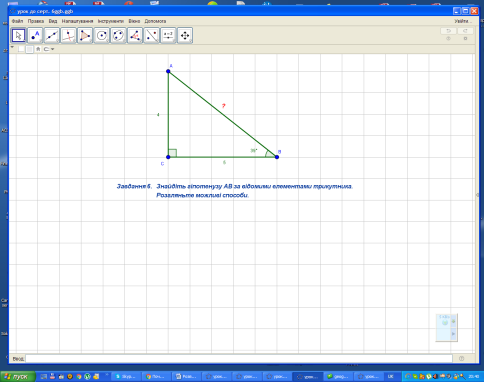
Завдання 6.

 

 

3. Завдання за готовими малюнками за презентацією (слайди 13,14).

 

 

 

 

IV. Застосування знань, умінь, навичок.

 

1. Зараз я запрошую вас у мандрівку.     Великий Піфагор говорив :

« Світ, що нас оточує, - це світ геометрії».

-  То ж давайте його пізнавати!

-  Чим будемо мандрувати? Як і всі мрійники – на повітряній кулі.   Земля як на долоні, коли ти в небі на повітряній кулі!

 

Але спочатку розв’яжемо задачу (слайд 15).

Задача 1. Як далеко видно з повітряної кулі, що піднялася на висоту 4 км над Землею (радіус Землі приблизно дорівнює 6370 км).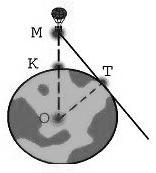 
Розв'язання.
1. За теоремою про властивість дотичної до кола, дотична перпендикулярна радіусу, проведеному в точку дотику, тобто  OTM = 90 ^о. .

2.  MO = 6370 +4 = = 6374 км.

3. За теоремою Піфагора: 
MT ² + OT ² = MO ² 
MT ² = MO ² - OT ² 
MT = 112,9 км 

Полетіли!

 

2. Ось наша

Кинашівка!

 

 (слайд 16)                                                                                                                                   

 

 

 

 

 

 

 

Наша рідна школа (слайди 17,18) .                              Де школа - там задачі!

                                                                                         (на 2 варіанти)

Задача 2. Знайти довжину драбини, прикладеної до будинку, якщо один її кінець знаходиться на відстані 4м від будинку, а другий на  зіткненні стіни і даху. Висота будинку дорівнює 8м.

 

Задача 3. Ширина  фронтона   7 м, довжина крокви 4,5 м. Під яким           кутом крокви нахилені до стелі ?

 

3. В центрі села знаходиться пам’ятний знак на місці церкви. Відомо, що пам’ятний знак було встановлено у ХІХ столітті (слайд19).

 

До реставрації.

 Реставрований.

 

 

 

 

 

 

 

 

 

 

 

Задача 4. Знайдіть кут підйому  дороги від мосту до пам'ятника, якщо на        відстані 200 м висота підйому становить 8 м.

                                                           Розв'язання.

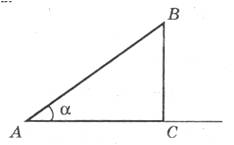1. На рисунку α — кут підйому дороги, АС горизонтальна пряма.

2. Проведемо , тоді ВС — висота підйому дороги.

3. За умовою АВ=200 м, ВС=8 м. Кут α знайдемо з прямокутного трикутника ABC,

.

Тоді α=2°18'.

Відповідь. Кут підйому дороги приблизно дорівнює 2°18'.

 

 

4. Від цього історичного місця спускаємось вниз до річки (слайд 20).

   

 

    

 

 

 

 

 

 

 

Задача 5.  На березі річки тополя росла та вітру порив її стовбур зламав.

                  Тополя упала і стовбур її кут прямий з течією річки утворив.

        Памятайте у тому місці ріка 4 фути була шириною.

        Верхівка схилилась до краю, залишивши 3 фути всього під     водою.

        Скажіть, тополя якої була висоти ?

(1фут = 0,3м.)

 

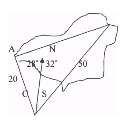
Задача 6. Знайти ширину водоймища між деревами, одне з яких знаходиться на відстані 20 м від нашого місцезнаходження на мосту і відхилене на захід на 32 °, а друге — відхилене на схід на кут 28 ° і знаходиться на відстані 50 м від нас.

 

Дано: ∆АВС, ВС = 50 м, АС = 20 м, АСВ = 60. Знайти: АВ

 

Розв'язання.

1. Проведено висоту AD BC.

2. ∆АDC: D = 90°, DC=AC∙cos60°=10 (м)
3. AD =AC∙sin60°=20:2 = 10 (м).

4. За аксіомою планіметрії : ВС= BD + CD, тому BD = ВС - CD = 40(м).

5. ∆ABD:  D= 90°. За теоремою Піфагора:

АВ² = AD² + BD² = 300 +1600 = 1900; АВ = 10(м)

Відповідь: 10м.

 

5. Гарна річка! Біля річки є цілюще джерело, дбайливо доглянуте мешканцями села  та учнями нашої школи  (слайд 21).

 

 

       

 

 

Якщо пощастить, то можна помилуватись і ніжними квітами латаття

 ( лотоси)

    

 

  Розглянемо стародавню індуську задачу 7 про лотос (слайд 22).

 Над озером тихим

Висотою з півфута підіймалась

 лотоса квітка, яка росла одиноко.

Та вітер скаженим поривом відніс її в бік.

І не стало видно квітки над водою.

Знайшов же її тільки рибалка ранньою весною в двох футах від місця,

де вона росла.

                                                           Яка в цьому місці на озері води глибина?

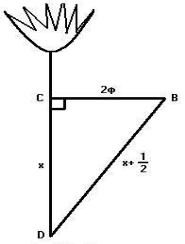                                      Розв’язання.

               Нехай CD = х футів, тоді відстань від лотоса до точки B - (х+0,5)футів.        Ця відстань дорівнює гіпотенузі прямокутного трикутника BCD. За теоремою Піфагора маємо:

ВD²=DС²+ВС²,отже: (х + 0,5)² = 2² + х²;

                                     х² + х + 0,25=4 + х²,

                                     х = 3,75.

                                Відповідь: 3,75 фути.

 

 

 

 

Наша мандрівка закінчується.

 

V.  Підведення підсумку уроку.

 

1. Сьогодні ми проводимо останній урок з даної теми. Я хочу запропонувати розгадати кросворд і знайти слово, з якого ми починали вивчення даної теми. (Роздати заготовлені кросворди) (слайд 23).

           1. Назва прямокутного трикутника зі сторонами 3, 4, 5.

           2. Учений, ім’ям якого названа теорема про суму квадратів катетів прямокутного трикутника.

           3. Острів, на якому народився цей учений.

           4. Катет, який не лежить проти даного кута.

           5. Там Піфагор прожив 12 років.

           6. Сторона прямокутного трикутника, яка лежить проти прямого     

               кута.

           7. Кількість биків, принесено Піфагором у жертву богам після

доведення теореми.

1
			2
								3
						4
				5
	6
								7

 

 

 

 

 

 

 

 

2. Що нового на уроці ви дізнались?

3. Закінчимо урок, згадавши вчення Піфагора, адже воно так нам необхідне в житті (слайд 24).

• Твори велике, не обіцяючи великого
• Нічому не дивуйся
• Тимчасова невдача краща від тимчасової удачі
• Не заплющуй очі, коли хочеш спати, не проаналізувавши своїх учинків за минулий день
• Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями
• Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом повинна бути повага до самого себе
• Лише неблагородна людина здатна в очі хвалити, а поза очі злословити
• Усе в світі підкоряється числам

 

4. Оцінювання учнів.

 

VІ. Домашнє завдання.

Повторити тему «Розв'язування прямокутних трикутників».

Скласти і розв’язати 1-2 практичні задачі на розв’язування трикутників.