Урок "Теорема Фалеса. Середня лінія трикутника та середня лінія трапеції. Розв’язування задач"

 

 

 

 

 

 

Теорема Фалеса. Середня лінія трикутника та середня лінія  трапеції. Розв’язування задач.

 

 

 

 

Урок з геометрії у 8 класі

вчителя математики

 

 

 

 

 

 

 

 

 

 

 

 

Мета уроку:

Навчальна:

-  повторити, систематизувати та узагальнити знання учнів щодо середньої лінії
трапеції та трикутника; теореми Фалеса;

- формувати вміння учнів застосовувати здобуті знання на практиці та показати практичне застосування геометрії в повсякденному житті;

- формувати просторові уявлення, розвивати логічне мислення.

Розвивальна:

• розвивати уміння учнів розв’язувати задачі на застосування теореми про середню лінію.

Виховна:

• виховувати наполегливість у навчальній праці та інтерес до геометрії.

Основні завдання:

• здійснити повторення властивостей середніх ліній трикутника та трапеції через усне розв’язання задач за готовими малюнками;
• домогтися від учнів робити правильні геометричні рисунки за умовами задач практичного спрямування, а також обґрунтовувати їх спираючись на життєвий досвід та знання властивостей геометричних фігур.

Засоби: картки із завданнями; підручник (М.І.Бурда,Н.А.Тарасенкова «Геометрія 8»); мультимедійна презентація, креслярський набір, крейда.

 

Епіграфи до  уроку

 

Блаженство тіла полягає у здоров'ї,

блаженство розуму - в знаннях

Фалес

 

Геометрія навколо нас

 

ХІД УРОКУ

I. Організаційний етап

ІІ. Формулювання мети і завдань уроку

На сьогоднішньому уроці ми з вами закріпимо теорему Фалеса,  поняття про середні лінії трикутника та трапеції; навчимося застосовувати набуті знання та вміння до розв’язування задач.  Зробимо екскурс в історію з життя Фалеса. Проаналізуємо чи отримала дана тема подальший розвиток і застосування у житті людини.

 

IIІ. Перевірка домашнього завдання.

Взаємоперевірка домашніх тестових завдань №2, 3  ст.67.

(Учні міняються зошитами. Правильні відповіді до задач висвітлюються через проектор, а учні олівцем ставлять «+» або «-».) (слайд 3)

Відповідь до:

 Тесту №2

• 1. Б; 
• 2. А; 
• 3. В; 
• 4. А; 
• 5. Г.

Тесту №3

• 1. Б; 
• 2. В; 
• 3. Б; 
• 4. Г; 
• 5. В.

 

Учитель: оскільки урок є підсумковим з тем «Теорема Фалеса», «Середня лінія трикутника», «Середня лінія трапеції», то вини­кає необхідність повторення, узагальнення та систематизації набутих знань, умінь під час вивчення теми.

Далі вчитель проводить з учнями усне бліцопитування (слайд 4)

• Сформулюйте теорему Фалеса.
• Що таке середня лінія трикутника?
• Сформулюйте властивості середньої лінії трикутника.
• Якщо всі середні лінії трикутника рівні, то яким буде цей трикутник?
• Яка залежність між периметром даного трикутника та трикутника утвореного його середніми лініями?
• Дайте означення трапеції.
• Які види трапеції ви знаєте?
• Що таке середня лінія трапеції?
• Сформулюйте властивість середньої лінії трапеції.
• Скільки середніх ліній можна побудувати в трикутнику? А в трапеції?

ІV. Актуалізація опорних знань

Задачі за готовим малюнками.

За допомогою презентації, учні усно розв’язують задачі і дають відповіді. За кожну правильну відповідь учень отримує смайлик на щоденник      (як додатковий бал до оцінки за урок)

(Усні вправи. Слайди № 6, 7, 8, 9, 10, 11)

 

Ми з вами вивчаємо геометрію уже другий рік. Кожен з вас переконався, який це цікавий, багатогранний розділ математики.

Але завжди виникає питання: а чи знадобляться мені ці знання у моєму житті? Для цього давайте поглянемо на наступний слайд. (слайд 12)

 

V. Мотивація

Прийом « Проблемне запитання»

Учитель: Як ви вважаєте, чи можна на практиці, не застосовуючи безпосередню вимірювання, а використовуючи тільки знання з геометрії, визначити довжину або ширину заболоченого місця?

І на це питання нам в кінці уроку дасть відповідь один учень, якому ця задача задавалась, як індивідуальне домашнє завдання.

 

VІ. Закріплення і застосування навичок та вмінь

Розв’язування задач.

Для цього ви об’єднаєтесь в пари, кожна пара отримає картку із задачею. Отриману при розв’язуванні задачі відповідь знаходите у таблиці, а навпроти – літеру.

Номер завдання на карточці, це порядковий номер літери у загадковому слові. Розгадка всього слова залежить від роботи всього класу, як команди.

 

Розв’язування задач: 4 картки і 1 на дошці (слайди 13-16)

Картка 1.

 

 

 

 

 

 

Відповідь: 40см, буква М

 

 

 

Картка 2

 

  Відповідь: 12см, 12см, 12см,  60⁰, буква І

 

 

 

 

 

 

Картка 3.

Відповідь: 17см, 19см, 21см, буква Л

 

 

 

 

 

Картка 4.

 

 

 

 

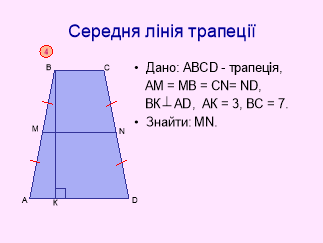
Відповідь: 10см, буква Е

 

 

Картка 5. Задача практичного змісту

Робота з підручником №369, ст.51

Умова задачі:

Над входом у дачний будинок є навіс. Згодом виникла потреба поставити підпори до середини навісу (точка F на малюнку 176). Як, не вимірюючи, знайти довжину підпори (відрізка EF), якщо відповідні краї навісу віддалені від поверхні землі на 2,5 м і 3,5 м? Подумайте, поміркуйте і зробіть геометричний малюнок до цієї задачі так, щоб за готовим кресленням ми могли розв’язати задачу

 

 

1. Учні пояснюють, чому саме такий малюнок (чому треба зобразити прямокутну трапецію,чому FE – середня лінія).

2. Обчислюють довжину підпори  FE, як довжину середньої лінії трапеції.

FE = (2,5+3,5)/2.

Відповідь: довжина підпори 3 метри, буква Т

 

Відповідь	Буква слова
18см, 40см, 66см	О
3м	Т
60см	П
7см	К
12см, 60о	І
17см, 19см, 21см	Л
16см, 24см, 28см	Я
10см	Е
3,5м	З
40см	М

 

Отримане слово – Мілет. Що це? Це давньогрецьке місто-держава на узбережжі Егейського моря, з якого походить Фалес.

Про Фалеса Мілетського нам підготували невеличку історичну довідку у вигляді мультимедійної презентації. Учень, що підготував презентацію, демонструє її.

 

А тепер повернемось до нашої задачі « Практичність теорії »

 

Учень, якому ця задача була на домашнє опрацювання виходить до дошки і пояснює її розв’язання(умова задачі попередньо замальована на відкидній дошці або ватмані).

На мал. зображено заболочене місце. Добудуємо прямі ОР, ОF та РF, що виходять з довільної точки О.

1.Виміряти ОР, ОF, знайти  середини цих відрізків, виміряти довжину середньої лінії трикутника РОF

2.Обчислити відстань між пунктами Р та F, як основу трикутника використовуючи властивість середньої лінії.

3.Виміряти відстані РМ і NF. Протяжність заболоченого місця обчислити за формулою МN=PF-(PM+NF).

Додаткове завдання  в групах (за рахунок вільного часу). Конверти з прямокутними трикутниками і завданням роздаються учням.

 

ЦІКАВА ЗАДАЧА

Скласти трапецію:

Група 1 – з  чотирьох прямокутних трикутників;

Група 2 –  із трьох прямокутних трикутників;

Група 3 –  із двох прямокутних трикутників.

Підказки на слайдах

 

 

 

 

VІІ.Підбиття підсумків уроку.

 

Як на вашу думку, знання із даної теми знайдуть практичне застосування у майбутньому вашому житті?

Чи задоволені ви своєю роботою на уроці?

Сподіваюся що на цьому уроці ви ще раз переконалися у справедливості відомого висловлювання:«Геометрія навколо нас». І маю надію що при нагоді вам вдасться скористатися знаннями здобутими на уроках геометрії, принаймні мені б цього дуже хотілося. Прошу здати щоденники на оцінки.

 

VІІІ.Домашнє завдання.

§6,7-повторити №297 (обов’язкове завдання для всіх,середній рівень), №354 - виконують учні, які бажають оцінку достатнього рівня),  №366 (завдання високого рівня).