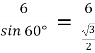Розробка уроку "Розв'язування прямокутних трикутників"







|
Косинусом гострого кута прямокутного трикутника називається ... |
|
Тангенсом гострого кута прямокутного трикутника називається ... |
|
Синусом гострого кута прямокутного трикутника називається ... |
|
Сторона, прилегла до прямого кута прямокутного трикутника... ... |
|
Відношення протилежного катета до прилеглого у прямокутному трикутнику... |
|
Відношення прилеглого катета до гіпотенуз у прямокутному трикутнику... |
|
Відношення протилежного катета до гіпотенузи у прямокутному трикутнику... |
|
Трикутник, що має прямий кут… |
|
Ромб, у якого всі кути рівні… |
|
Трикутник, у якого дві сторони рівні… |
|
Відрізок, що сполучає середини бічних сторін трапеції… |
|
Твердження, що потребує доведення… |
|
Промінь, який виходить з вершини кута і ділить його навпіл… |
|
Прямокутник, у якого всі сторони рівні… |
|
Відрізок, що сполучає дві точки на колі… |
|
Прямі, які перетинаються під прямим кутом… |

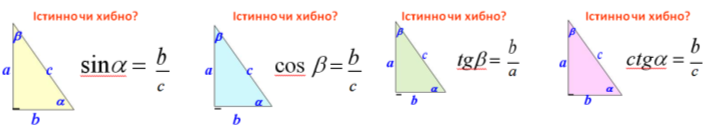
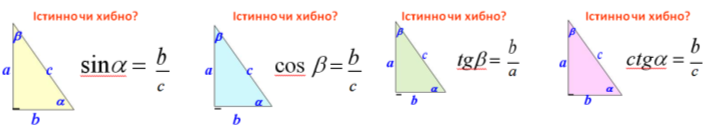
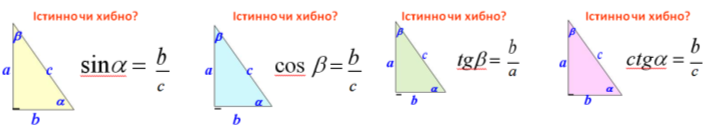
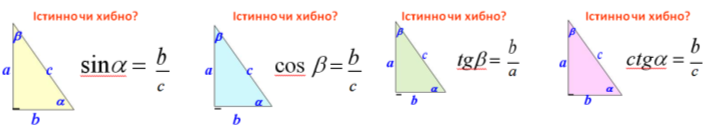
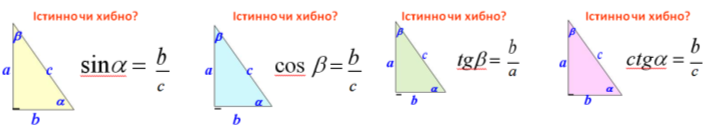






Дата: ___/___/___ Клас: 8 Предмет: геометрія
Тема. Розв’язування прямокутних трикутників
Мета уроку:
- навчати учнів застосовувати правила знаходження катета і гіпотенузи при розв'язуванні задач;
- узагальнення, систематизація та закріплення знань про теорему Піфагора;
- застосування набутих знань і вмінь у практичній діяльності;
- розвиток вмінь аналізувати, робити висновки, знаходити власні способи розв’язання;
- формування компетентностей:
- соціальних (розвиток пізнавальної активності учнів, робота в команді, усвідомлення власного внеску в спільну роботу, вміння брати відповідальність),
- комунікативних (формування власної точки зору, розвиток культури мовлення, вміння доводити власну позицію);
- виховування активності, уваги, кмітливісті, самостійністі;
- прищеплення інтересу до математики.
Тип уроку: формування вмінь і навичок учнів.
Обладнання: картки з індивідуальним завданням, демонстраційно-креслярське приладдя, картки з запитаннями для актуалізації знань, матеріали для кластера.
Хід уроку
Світ, що нас оточує, - це світ геометрії. Т Тож давайте його пізнавати!
Піфагор
Привітання
Перевірка готовності до уроку.
ІІ. Перевірка домашнього завдання
Взаємоперевірка
№ 725


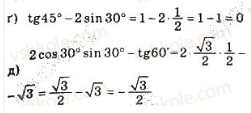
Самостійна робота з подальшою взаємоперевіркою

ІІІ. Актуалізація опорних знань
Повторимо матеріал, вивчений на уроках. Проведемо гру. (діти поділені на групи за їх бажанням) Наша гра математична. Учні витягують завдання з мішечка і дають відповідь групою протягом 10 секунд.
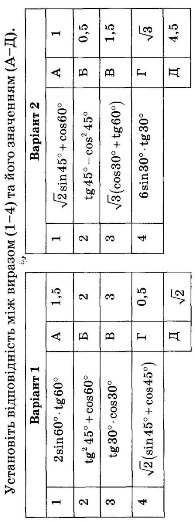
- Косинусом гострого кута прямокутного трикутника називається ...
- Тангенсом гострого кута прямокутного трикутника називається ...
- Синусом гострого кута прямокутного трикутника називається ...
- Сторона, прилегла до прямого кута прямокутного трикутника... ...
- Відношення протилежного катета до прилеглого у прямокутному трикутнику...
- Відношення прилеглого катета до гіпотенуз у прямокутному трикутнику...
- Відношення протилежного катета до гіпотенузи у прямокутному трикутнику...
- Трикутник, що має прямий кут…
- Ромб, у якого всі кути рівні…
- Трикутник, у якого дві сторони рівні…
- Відрізок, що сполучає середини бічних сторін трапеції…
- Твердження, що потребує доведення…
- Промінь, який виходить з вершини кута і ділить його навпіл…
- Прямокутник, у якого всі сторони рівні…
- Відрізок, що сполучає дві точки на колі…
- Прямі, які перетинаються під прямим кутом…
Вправа «Істинно чи хибно?»
|
|
|
|
Істинно чи хибно? |
|
|
|
|
Істинно чи хибно? |
|
|
|
|
Істинно чи хибно? |
|
|
|
Істинно чи хибно? |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
||||||||
|
|
|
b |
|
|
b |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
с |
sin |
|
|
|
с |
cos |
a |
|
|
с |
tg |
a |
|
|
с |
ctg |
||||
|
a |
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
c |
||||||||||||
|
|
|
c |
|
|
c |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
||||
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ІV. Вивчення нового матеріалу
План вивчення теми
- Що означає «розв'язати трикутник».
Розв'язати трикутник — означає знайти його невідомі сторони й кути за відомими сторонами і кутами.
-
Розв'язування прямокутного трикутника ABC (
 C = 90°).
C = 90°).
-
За гіпотенузою і гострим кутом (АВ = с,
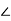 A =
A = 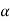 ): 1)
): 1) 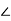 B = 90°-
B = 90°- 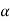 ; 2) АС = сcos
; 2) АС = сcos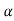 ; 3) ВС = сsin
; 3) ВС = сsin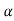 .
.
Приклад:
|
C B |
Дано: АВ = 10,
Знайти: Розв’язання
АС = 10 • cos 60° = 10 • 0,5 = 5 (см)
ВС = 10 • sin 60° = 10 • |
-
За катетом і гострим кутом, протилежним катету (ВС = а,
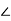 А =
А = 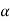 ):
):
-
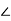 B = 90°-
B = 90°- 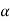 ; 2) АВ =
; 2) АВ = 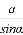 ; 3) АС =
; 3) АС =  .
.
|
C B |
Дано: ВС= 6,
Знайти: Розв’язання
AВ =
АС = |
-
За катетом і гострим кутом, прилеглим до катета (ВС = a,
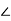 B =
B = 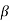 )
)
-
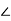 A = 90°-
A = 90°- 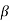 ; 2) АВ =
; 2) АВ = 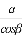 ; 3) AC = a tg
; 3) AC = a tg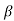 .
.
|
C B |
Дано: ВС= 6,
Знайти: Розв’язання
AВ =
АС = |
- За гіпотенузою і катетом (АВ = с, ВС = а):
1) АС = ![]() ; 2) sinA =
; 2) sinA = ![]() ; 3)
; 3) ![]() B = 90° -
B = 90° - ![]() A.
A.
|
C B |
Дано: ВА= 5, ВС = 3
Знайти: Розв’язання
АС =
sinA =
|
- За двома катетами (ВС = a, АС = b):
1) AB = ![]() ; 2) tgА =
; 2) tgА = ![]() ; 3)
; 3) ![]() = 90°-
= 90°- ![]() A.
A.
|
C B |
Дано: ВС = 6, АС = 8
Знайти: Розв’язання
АС =
tgА =
3) |
Складання кластера
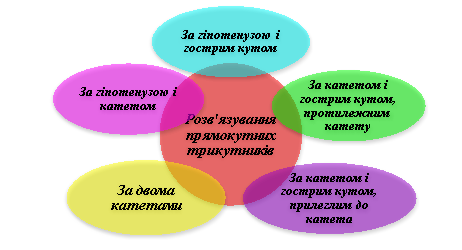
V. Засвоєння нових знань і вмінь
Виконання письмових вправ
- Розв'яжіть прямокутний трикутник за гіпотенузою і гострим кутом с = 8, α = 30°.
- Розв'яжіть прямокутний трикутник за катетом і гострим кутом а = 2, β = 45°.
-
Розв'яжіть прямокутний трикутник за гіпотенузою і катетом: с = 9
 , а = 9.
, а = 9.
-
Розв'яжіть прямокутний трикутник за двома катетами: а = 6
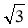 , b = 6.
, b = 6.
- Відрізок BD — висота прямокутного трикутника ABC, проведена до гіпотенузи. Розв'яжіть трикутник ABC, якщо:
a) BD = 4![]() ,
, ![]() DBC = 60°; 5) AD = 9,
DBC = 60°; 5) AD = 9, ![]() C = 10°.
C = 10°.
- У рівнобічну трапецію вписано коло, радіус якого дорівнює 12 см. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 25 см.
- У колі з центром О і радіусом 10 см проведено хорду АВ довжиною 16 см. Із центра кола до хорди проведено перпендикуляр, який перетинає хорду в точці Е, а коло — у точці F. Знайдіть довжину відрізка EF.
- Радіуси двох кіл дорівнюють 8 см і 3 см, а відстань між їх центрами — 13 см. Знайдіть довжину їх зовнішньої спільної дотичної.
VI. Підсумки уроку
Фронтальна бесіда
Які елементи слід знати додатково, щоб мати можливість розв'язати трикутники, що зображені на рисунку
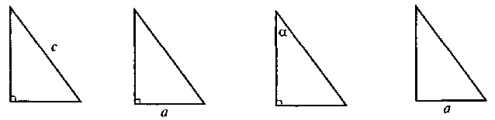
Метод «Похвали себе»
- Чи з’явилося почуття самоповаги від твоєї роботи на уроці?
- Похвали себе одним реченням.
VІІ.Домашнє завдання
§17 (опрацювати),
№№ 754(а, б)
Повторити властивості рівнобічної трапеції, прямокутної трапеції, метричні співвідношення в прямокутному трикутнику.
1


про публікацію авторської розробки
Додати розробку