8 клас КР № 2 Трапеція. Центральні та вписані кути. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції
___________________________________________________________________________________________________
8 клас КР № 2 Трапеція. Центральні та вписані кути. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції Варіант І

- Укажіть бічні сторони трапеції, зображеної на малюнку.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Знайдіть градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює
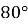 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
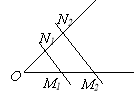
Дано:
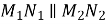 ,
, 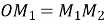 ,
, 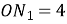 см.
см.
Знайти: ![]() .
.
А. 6 см. Б. 9 см. В. 8 см. Г. 7 см.
-
Знайдіть кути
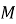 і
і 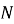 чотирикутника
чотирикутника 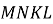 , вписаного в коло, якщо
, вписаного в коло, якщо 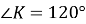 ,
, 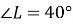 .
.
- Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, сторонами якого є середні лінії даного трикутника.
- Середня лінія трапеції дорівнює 10 см. Знайдіть основи трапеції, якщо одна з них на 2 см більша за другу.
- У рівнобічну трапецію, периметр якої 28 см, вписано коло. Знайдіть бічну сторону трапеції.
-
У прямокутній трапеції тупий кут дорівнює
 , а більша бічна сторона і більша основа дорівнюють по 16 см. Знайдіть меншу основу трапеції.
, а більша бічна сторона і більша основа дорівнюють по 16 см. Знайдіть меншу основу трапеції.
- Діагональ рівнобічної трапеції ділить її тупий кут навпіл, а середню лінію – на відрізки 4 см і 5 см. Знайдіть периметр трапеції.
___________________________________________________________________________________________________
8 клас КР № 2Трапеція. Центральні та вписані кути. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції Варіант ІІ
-
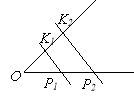
 Укажіть основи трапеції, зображеної на малюнку.
Укажіть основи трапеції, зображеної на малюнку.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Знайдіть градусну міру центрального кута, якщо відповідний йому вписаний кут дорівнює
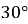 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Дано:
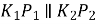 ,
, 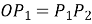 ,
, 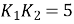 см.
см.
Знайти: ![]() .
.
А. 10 см. Б. 12 см. В. 9 см. Г. 15 см.
-
Знайдіть кути
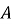 і
і 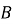 чотирикутника
чотирикутника 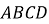 , вписаного в коло, якщо
, вписаного в коло, якщо 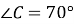 ,
, 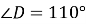 .
.
- Знайдіть периметр трикутника, якщо його середні лінії дорівнюють 5 см, 7 см і 8 см.
- Середня лінія трапеції дорівнює 12 см. Знайдіть основи трапеції, якщо одна з них на 4 см менша від другої.
- Коло вписане в рівнобічну трапецію. Знайдіть периметр трапеції, якщо її бічна сторона дорівнює 5 см.
-
У прямокутній трапеції гострий кут дорівнює
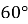 , а більша основа і більша бічна сторона дорівнюють по 18 см. Знайдіть меншу основу трапеції.
, а більша основа і більша бічна сторона дорівнюють по 18 см. Знайдіть меншу основу трапеції.
- Діагональ рівнобічної трапеції ділить її гострий кут навпіл, а середню лінію – на відрізки 3 см і 4 см. Знайдіть периметр трапеції.
___________________________________________________________________________________________________
___________________________________________________________________________________________________
8 клас КР № 2Трапеція. Центральні та вписані кути. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції Варіант ІІІ
-
 Укажіть основи трапеції, зображеної на малюнку.
Укажіть основи трапеції, зображеної на малюнку.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Знайдіть градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює
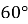 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
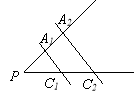
Дано:
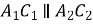 ,
, 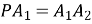 ,
, 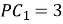 см.
см.
Знайти: ![]() .
.
А. 9 см. Б. 6 см. В. 7 см. Г. 5 см.
-
Знайдіть кути
 і
і 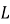 чотирикутника
чотирикутника 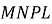 , вписаного в коло, якщо
, вписаного в коло, якщо 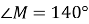 ,
, 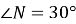 .
.
- Сторони трикутника дорівнюють 8 см, 12 см і 14 см. Знайдіть периметр трикутника, сторонами якого є середні лінії даного трикутника.
- Середня лінія трапеції дорівнює 6 см. Знайдіть основи трапеції, якщо одна з них на 2 см менша від другої.
- Коло вписане в рівнобічну трапецію, периметр якої 24 см. Знайдіть бічну сторону трапеції.
-
У прямокутній трапеції тупий кут дорівнює
 , більша бічна сторона – 10 см, а більша основа – 8 см. Знайдіть меншу основу трапеції.
, більша бічна сторона – 10 см, а більша основа – 8 см. Знайдіть меншу основу трапеції.
- Діагональ рівнобічної трапеції ділить її тупий кут навпіл. Менша основа трапеції дорівнює 10 см, а бічна сторона – 16 см. Визначте довжини відрізків, на які діагональ ділить середню лінію трапеції.
___________________________________________________________________________________________________
8 клас КР № 2Трапеція. Центральні та вписані кути. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника і трапеції Варіант ІV
-
 Укажіть бічні сторони трапеції, зображеної на малюнку.
Укажіть бічні сторони трапеції, зображеної на малюнку.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Знайдіть градусну міру центрального кута, якщо відповідний йому вписаний кут дорівнює
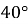 .
.
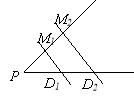 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Дано:
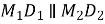 ,
, 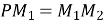 ,
, 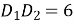 см.
см.
Знайти: ![]() .
.
А. 14 см. Б. 10 см. В. 8 см. Г. 12 см.
-
Знайдіть кути
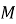 і
і 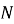 чотирикутника
чотирикутника 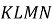 , вписаного в коло, якщо
, вписаного в коло, якщо  ,
, 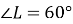 .
.
- Знайдіть периметр трикутника, якщо його середні лінії дорівнюють 4 см, 5 см і 6 см.
- Середня лінія трапеції дорівнює 8 см. Знайдіть основи трапеції, якщо одна з них на 4 см більша за другу.
- Коло вписане в рівнобічну трапецію. Знайдіть периметр трапеції, якщо її бічна сторона дорівнює 7 см.
-
У прямокутній трапеції гострий кут дорівнює
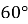 , а більша основа – 10 см, більша бічна сторона – 8 см. Знайдіть меншу основу трапеції.
, а більша основа – 10 см, більша бічна сторона – 8 см. Знайдіть меншу основу трапеції.
- Діагональ рівнобічної трапеції ділить її гострий кут навпіл. Більша основа трапеції дорівнює 14 см, а бічна сторона – 8 см. Визначте довжини відрізків, на які діагональ ділить середню лінію трапеції.
___________________________________________________________________________________________________


про публікацію авторської розробки
Додати розробку
