Розробка уроку «Симетрія відносно прямої»

Симетрія - це ідея, за допомогою якої людина намагається пояснити і створити порядок, красу, досконалість», - слова Г. Вейля

Тема . Симетрія відносно прямої.

Мета. Ознайомити учнів із  поняттям «симетрія відносно прямої»;формувати вміння виконувати перетворення симетрії фігури відносно прямої; знаходити вісь симетрії в  різних геометричних фігурах; розвивати вміння застосовування інформаційних технологій для перетворення симетрії фігури відносно прямої; допомогти учням усвідомити  практичну  значимість навчального матеріалу;активізувати взаємодію між учнями; створити умови для творчої самореалізації особистості;виховувати інтерес до математики та інформатики.

 

Програмні засоби й цифрові ре­сурси:

• комп’ютер ,мультимедійний проектор,ноутбук
• програми : Microsoft Power Point, DG.

 

 

Тип уроку: засвоєння нових знань.

Хід уроку

І. Організаційний момент.(1 хв)

1.Вітання вчителя.

 В. Доброго дня!

 (Черговий перед початком уроку збирає аркуші з домашнім завданням:побудова фігури симетричної даній відносно  точки)

Ч. Домашнє завдання виконали всі учні. Питань по домашній роботі немає.

В. Добре. На минулому уроці ми навчилися будувати фігури,симетричні даним відносно точки. А чи має ця тема відношення до нашого повсякденного життя?Про це нам розповість у своїй презентації Крижня Марина.

Повідомлення

Математично строге визначення симетрії сформувалося порівняно  недавно – в 19 столітті. В найбільш простій трактовці відомого німецького математика Германа Вейля (1855 – 1955) сучасне визначення симетрії  виглядає так: симетричним називається такий об’єкт, який можна якось змінювати, отримуючи в результаті те ж, з чого почали. Сучасна уява про симетрію припускає незмінність об’єкту по відношенню до якихось перетворень, які виконуються  над ним.

Відеопроект «Симетрія відносно точки»

 

В. Дякую за цікаву інформацію.

ІІІ. Нова тема : «Симетрія відносно прямої»

В. Сьогодні ми поговоримо про ще один вид перетворення – «Симетрія відносно прямої». Відкрили зошити,записали число і тему нашого уроку «Симетрія відносно прямої»

З цим поняттям ми теж знайомі ще з 6 класу,то ж на уроці ми згадаємо поняття «симетрія відносно прямої»,познайомимося з фігурами симетричними відносно прямої та будемо знаходити іхні осі симетрії,будемо будувати фігури симетричні даним відносно прямої використовуючи  знайому вам програму «Динамічна геометрія».

 Тему «Симетрія відносно прямої» досліджувала самостійно Щербак Аліна,яка і нагадає нам основні означення.

За допомогою програми Microsoft Power Point знайомство з новою темою.

І.  Щоб побудувати точку, симетричну точці М відносно даної прямої

     1 проведемо через неї пряму МО, перпендикулярну даній прямій а ;

      2 відкладемо  на ній відрізок ОМ₁, рівний відрізку ОМ.

В.Будь ласка виконайте побудову малюнка в зошиті. Виконали?

Запишіть план побудови.

 

Побудова М₁

1. МО   _┴  а ;

2. ОМ₁   = ОМ.

3.  М₁  симетрична точці М

 

Означення симетричних точок

Дві точки М и М₁ називаються симетричними відносно прямої а, якщо ця пряма проходить через середину відрізка ММ₁   і перпендикулярна до нього.

     М

 

  а

    

    М₁

 

В.А зараз я пропоную виконати  в зошиті завдання  по варіантах І – а;ІІ – б;ІІІ – в; ІV – г

 

 

 

 

 

 

 

 

 

 

 

 

 

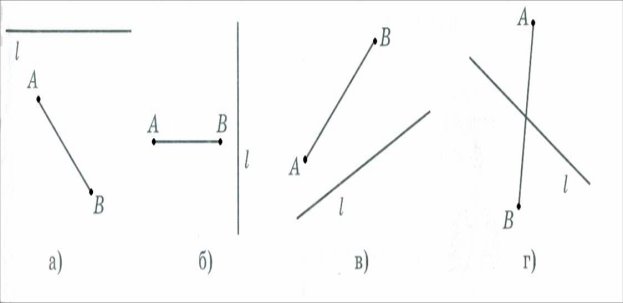
В. Перевірте правильність виконання завдань.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

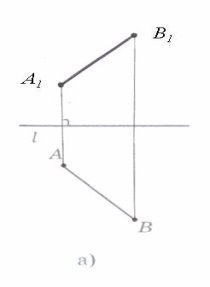
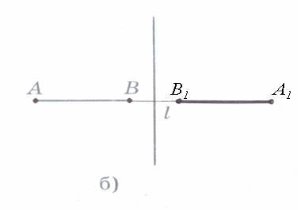
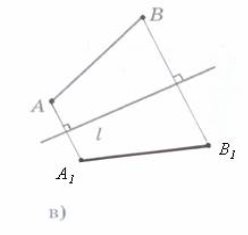
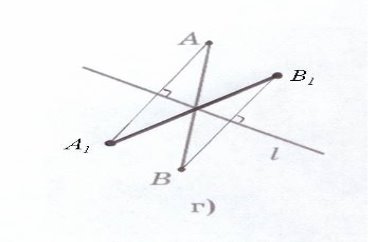
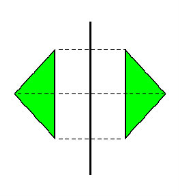Аліна.  Перетворення фігури F у фігуру F _1, при якому кожна її точка переходить в точку, симетричну відносно даної прямої, називається перетворенням симетрії відносно прямої a

 

 

 

 

 

.В. Які властивості мають точки симетричні відносно прямої?

 

 

В.

 

 

А тепер перейдемо до означення фігури симетричної відносно прямої

 

Аліна.

 

 

 

В. А зараз виконаємо завдання

 

В.Перевірте правильність виконання завдання.

 

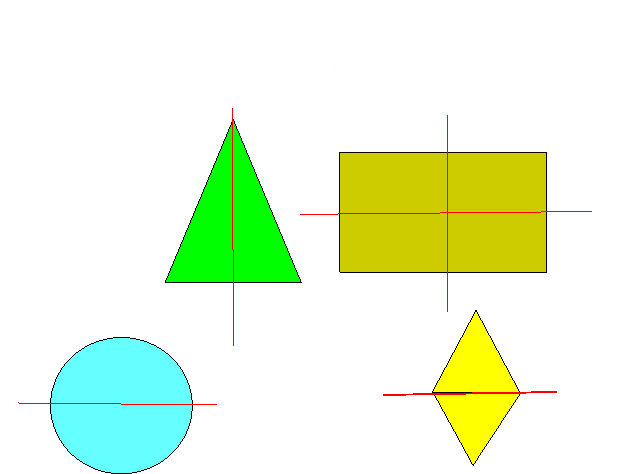
В.А зараз ми проглянемо відеопроект «Симетрія відносно прямої в нашому житті»,який підготувала Павленко В.

Перегляд відеопроекту.

 

Виконання завдань із використанням комп’ютера.

 

А зараз настав час зайняти свої місця за комп’ютером і виконати завдання.(робота в парах)

Картки покладені біля кожного комп’ютера перед уроком.

 

Картка-завдання

1.Побудуйте відрізок симетричний даному відносно даної прямої. Доведіть правильність побудови.

2.Побудуйте чотирикутник симетричний даному відносно заданої прямої. Доведіть правильність побудови.

3.Побудуйте коло,та проведіть  вісь симетрії,якщо це можливо. Якщо коло має декілька осей,то проведіть три.

4*Створити власний проект за темою «Симетрія відносно прямої»

 

ІV. Підведення підсумку уроку

1.За яких трьох умов точка А₁  буде  симетричною точці А.

2.Вісь симетрії фігури. Як її знайти?

3.Скільки осей симетрії має прямокутник,ромб?

Рефлексія .

Як би я оцінив свою роботу на уроці?

             -- «Я все зрозумів,можу працювати самостійно»

  -   «Мені була зрозуміла більша частина  завдань,але я ще іноді припускаюся помилок.

- «Я майже нічого не зрозумів,це все для мене складно»

Оцінки.

V. Домашнє завдання

1.Виконати проектну роботу “Чи владна симетрія над світом?”,  оформити її у вигляді презентації.

2.вивчити означення.

Так як в підручнику цих означень немає,я пропоную їх вивчити  за  картками консультантами, в яких також написано більш детально домашнє завдання.