Матеріали до уроків " Вектори на площині" 9 клас
Мета: сприяти формуванню та розвитку інтелектуальних та творчих компетентностей учнів під час вивчення та повторення теми «Вектори на площині»; зацікавити учнів математикою, встановлюючи зв´язки між математикою та іншими сферами життя; виховувати наполегливість та активність.
Скарбничка математичних ідей
Геометрія 9 клас.
Вектори на площині.
Підготувала
вчитель математики Шеремет В.П.
Мета: сприяти формуванню та розвитку інтелектуальних та творчих здібностей учнів під час вивчення та повторення теми «Вектори на площині»; зацікавити учнів математикою, встановлюючи зв´язки між математикою та іншими сферами життя; виховувати наполегливість та активність.
******************
Пропонований матеріал містить різні види діяльності на уроках геометрії у 9 класі,які можна використати при вивченні, повторенні та систематизації знань учнів з теми «Вектори на площині».
Математика не тільки приготує учня до вивчення природничих наук, не тільки навчить його мислити правильно й послідовно: вона ще, крім того, виховає в ньому безстрашного працівника, для якого праця і нудьга стануть взаємно несумісними поняттями. Д.І.Писарєв.
****************************
Математики мають особливий склад мислення. Але його можна виховати практично в кожної людини. Тільки починати треба рано. В.І.Арнольд.
***********************
Історична довідка:
Назву «вектор» (той, що несе) запровадив ірландський математик У. Гамільтон(1805-1865). Позначення ![]() для напрямленого відрізка вперше використав у 1806 р. швейцарський математик Ж.Арган(1768-1822). Починаючи з 1853 року вектор стали позначати однією буквою.
для напрямленого відрізка вперше використав у 1806 р. швейцарський математик Ж.Арган(1768-1822). Починаючи з 1853 року вектор стали позначати однією буквою.
Термін «модуль» походить від латинського слова modulus – міра. Вперше використав англійський математик Р. Котес(1682-1716). Знак модуля ввів у 1841 році німецький математик Вейєрштрасс(1815-1897).
Термін «колінеарний» походить від латинського сполучення:co(cum) - разом, спільно, lineo – лінія.
Термін «скалярний» походить від латинського scalaris,що означає – східчастий. Вперше його використав У. Гамільтон.
«Занурення в тему»(Основні поняття теми):векторні та скалярні величини, модуль вектора, одиничний вектор(орт), колінеарні вектори, протилежно напрямлені та однаково напрямлені вектори, правило трикутника, правило паралелограма, нульовий вектор, координати вектора, довжина вектора, скалярне множення, скалярний добуток векторів, скалярний квадрат вектора,
Вважай нещасним той день і ту годину, в які ти не засвоїв нічого нового або не додав до своєї освіти. Монтеск´є.
********************
«Перевір себе».
Тестові завдання:
-
Якщо
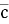 (-3;4), то модуль вектора дорівнює: а)1; б)5; в)
(-3;4), то модуль вектора дорівнює: а)1; б)5; в)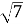 ; г)12; д)9.
; г)12; д)9.
-
Відомо, що
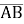 (-2;-8), А(3;-1). Тоді точка В має координати: а)(0,5;4,5), б)(-1;9), в)(-5;-7), г)(5;7), д)(1;-9).
(-2;-8), А(3;-1). Тоді точка В має координати: а)(0,5;4,5), б)(-1;9), в)(-5;-7), г)(5;7), д)(1;-9).
-
Якщо К(-1;2), В(3;7), то модуль вектора
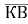 дорівнює: а)
дорівнює: а)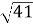 , б)3, в)12, г)11, д)
, б)3, в)12, г)11, д)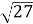 .
.
-
Якщо С(-6;8) і О – початок координат, то довжина вектора
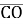 дорівнює: а)10, б)2, в)14. Г)2
дорівнює: а)10, б)2, в)14. Г)2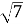 , д)3
, д)3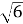 .
.
-
Якщо
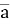 (1;4),
(1;4), 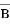 (3;-2) і сума цих векторів дорівнює: а)(5;1), б)(2;-6), в)(3;-8), г)(4;2), д)(-1;7).
(3;-2) і сума цих векторів дорівнює: а)(5;1), б)(2;-6), в)(3;-8), г)(4;2), д)(-1;7).
-
Вектори
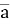 (х;-2) і
(х;-2) і 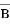 (-3;1) колінеарні, якщо: а)х=-5, б)х=5, в)х=6, г)х=-6, д) х=-7.
(-3;1) колінеарні, якщо: а)х=-5, б)х=5, в)х=6, г)х=-6, д) х=-7.
«Хай живе теорія!»
- Що таке вектор? Запис і позначення.
- Які дії можна виконувати з векторами?
- Як знайти координати вектора?
- Чому дорівнює модуль вектора? Записати формулу.
- Як помножити на число вектор, заданий своїми координатами?
- Які вектори називаються рівними?
- Які вектори називаються колінеарними?
- Які вектори називаються перпендикулярними?
- Поясніть, що таке кут між двома векторами.
- Як знайти скалярний добуток векторів за їхніми координатами?
- Чому дорівнює скалярний добуток векторів?
- Як знайти косинус кута між векторами?
Пам´ятайте! Якщо ви хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв´язувати задачі, то розв´язуйте їх! Д. Пойа.
«Мозковий штурм».
-
Знайти координати і модуль вектора
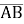 , якщо А(-8;3), В(0;-4).
, якщо А(-8;3), В(0;-4).
-
Кінцем вектора
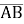 є точка В(-3;-2). Знайти координати точки А, якщо точка А лежить на осі абсцис і абсолютна величина вектора
є точка В(-3;-2). Знайти координати точки А, якщо точка А лежить на осі абсцис і абсолютна величина вектора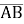 =7.
=7.
-
Дано вектори
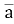 (-4;1),
(-4;1),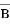 (3;-2). Знайти координати векторів
(3;-2). Знайти координати векторів 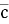 =-3
=-3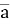 +4
+4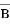 .
.
- Точки А(1;0), В(3;-2), С(-4;1) є вершинами трикутника. Обчислити косинуси кутів цього трикутника.
-
Дано точки М(3;-4), А(-1;2), К(0;-3). Обчислити: а)координати векторів
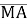 і
і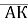 ; б)абсолютні величини векторів; в)косинус кута між векторами.
; б)абсолютні величини векторів; в)косинус кута між векторами.
-
Знайти значення х, при якому вектори
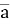 (х;3) і
(х;3) і 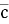 (3;2) а)перпендикулярні; б)колінеарні.
(3;2) а)перпендикулярні; б)колінеарні.
Не достатньо опанувати премудрість, потрібно ще вміти нею користуватися. Цицерон.
*********************
ВЕСЕЛІ СЛОГАНИ ПРО СЕРЙОЗНІ РЕЧІ:
*Не відкладай життя на завтра, будь першим сьогодні!
*Кожна тема з математики неповторна! Відкрий для себе її секрети!
*Змінюється все – досконалість математики незмінна! Відчуй задоволення від досконалості!
Людина може пізнати свої здібності лише застосувавши їх на справі. Сенека.
*********************
«Практика – велика сила!»
|
1.Знайдіть координати вектора |
2.Знайдіть модуль вектора |
|
3. Знайдіть координати вектора |
4.При якому значенні х вектори з задами координатами (3;-2) і (х;8) колінеарні? |
|
5.Знайдіть значення у, при яких вектори з координатами (у-4;3) і (2;1-2у) колінеарні? |
6. Знайдіть скалярний добуток векторів (1;3) і (4;0). |
|
7.Знайдіть кут між векторами з координатами (3;0) і (2;2). |
8. При якому значенні а вектори з координатами (4;а) і (-5;2) перпендикулярні? |
****************
- Дано вершини трикутника: А(1:1), В(4:1), С(4:5). Знайдіть косинуси кутів трикутника.
- Дано вершини трикутника: А(-2;1), В(-2;4), С(2;1). Знайдіть косинуси кутів трикутника.
Термінологічне завдання:
- Напрямлений відрізок, називається……….
- Щоб задати вектор, достатньо вказати…….
- Відстань між початком і кінцем вектора, називається…………..
- Довжина нуль-вектора дорівнює…………….
- Якщо два вектори паралельні одній прямій, то вони називаються…………………
- Якщо вектори співнапрямлені і мають рівні довжини, то вони називаються………
- Якщо відповідні координати двох векторів пропорційні, то такі вектори називаються…………………….
- Щоб помножити вектор на число, треба……………………………………………………
- Скалярний добуток двох векторів, заданих координатами дорівнює……………
- Якщо скалярний добуток двох векторів дорівнює нулю, то такі вектори називаються………………….
Практична робота:
-
На тіло діють сили
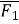 (1;5) і
(1;5) і 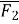 (-4;7). Знайдіть вектор рівнодійної сили.
(-4;7). Знайдіть вектор рівнодійної сили.
- Двоє учнів витягують човен на берег, тримаючи його за трос. Яка сила діє на човен, якщо один учень прикладає силу 100 Н, а другий – 120 Н?
- Північний вітер змінився на: 1)північно-східний; 2)північно-західний; 3)східний. Покажіть початковий і кінцевий напрям вітру та напрям його зміни.
- За допомогою векторів покажіть зміну середньодобової температури: 1)за два дні; 2)за тиждень.
Контрольна робота
-
Дано точки: Р(-1;0), А(-3;-2), Т(1;4). Обчислити: а)
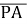 і
і 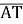 ; б)
; б)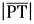 і
і 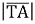 ; в)
; в)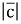 , якщо
, якщо 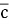 =3
=3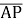 -2
-2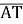 ; г)косинус кута між векторами
; г)косинус кута між векторами 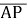 і
і 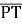 .
.
-
Знайти значення у, при якому вектори
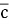 (-3
(-3 ;у),
;у), 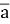 (-5
(-5 ;2
;2 ) а)колінеарні; б)перпендикулярні.
) а)колінеарні; б)перпендикулярні.
-
Модуль вектора
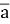 дорівнює 10. Його перша координата на 2 більша за другу. Знайдіть координати вектора
дорівнює 10. Його перша координата на 2 більша за другу. Знайдіть координати вектора 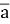 .
.
Література
- Журнал «Математика в школах України».
- Журнал «Відкритий урок. Розробки. Технології. Досвід.»
- Карпінська І.Й. Нестандартні уроки з математики. – Тернопіль: Підручники і посібники, 2000.
- Конфорович А.Г. Математичні софізми і парадокси. – К.: Рад. шк., 1983.
- Янченко Г.М. Сучасний урок з математики. – Тернопіль,1991.
- Козира В.М. Технологія уроку математики. –Тернопіль, 2002.
1

про публікацію авторської розробки
Додати розробку
