Збірник усних вправ і схем-узагальнень "З геометрією на ти" (7-9 класи)
Збірник усних вправ і схем-узагальнень з деяких тем геометрії 7-9 класів, містить у супроводі файл-презентацію, що вирішить проблему швидкого наочного зображення фігур, графіків, схем
- геометрією на ти doc
- геометрією на ти ppt
Н.О. Часницька
«З геометрією на ти»
(комплекс усних вправ і схем-узагальнень
з деяких тем геометрії для 7-9 класів)

Будівельнівський навчально-виховний комплекс: загальноосвітня школа І-ІІ ст.,
дошкільний навчальний заклад «Зернятко»
2017 р.
Зміст
Схеми-узагальнення для 7 класу
Схеми-узагальнення для 8 класу
Схеми-узагальнення для 9 класу
Вступ
В умовах системних змін в освіті, особливо актуальним стає забезпечення належного рівня математичної підготовки підростаючого покоління.
Математика має широкі можливості для інтелектуального розвитку особистості, в першу чергу - розвитку логічного мислення, просторових уявлень і уяви, алгоритмічної культури, формування вміння встановлювати причинно-наслідкові зв'язки, обґрунтовувати твердження, моделювати ситуації та ін. Математика є засобом вивчення фізики, хімії, інформатики та обчислювальної техніки, астрономії, біології, загальнотехнічних і спеціальних дисциплін, вона також є мовою техніки, а розвинене логічне мислення сприяє засвоєнню гуманітарних предметів.
Особливістю організації навчально-виховного процесу є орієнтація на досягнення всіма учнями максимально можливого для них рівня математичної.
Важливою умовою організації ефективного навчально-виховного процесу є вибір вчителем раціональної системи методів і прийомів активного навчання, використання нових інформаційних технологій у поєднанні з традиційними засобами. Особлива роль у навчанні математики належить системі задач і вправ, зокрема усних вправ за малюнками.
Усні вправи розвивають в учнів спостережливість, iнiцiативу, збуджують інтерес до вивчення математики. Під час виконання усних вправ учні закріплюють теоретичні знання, тренують пам’ять, підвищують логічну та загальноматематичну культуру. За допомогою усних вправ учитель налагоджує на уроках ефективний оперативний зворотний зв’язок з учнями, що дозволяє своєчасно контролювати процес оволодіння новими знаннями та формувати вміння й навички.
Провідною ідеєю використання усних вправ є створення на уроках математики умов для особистісного розвитку учнів, розвитку їх iндивiдуальностi.
Також важливою умовою навчання математиці є пошук зв’язків між поняттями та їх співставлення. У застосуванні цього прийому гарним помічником є складання схем-узагальнень для систематизації знань учнів. Схеми дозволяють наочно бачити спільні та відмінні сторони вивчених понять і геометричних фігур. Використання схем-узагальнень дозволяє розвивати в учнів здатність робити висновки та логічно завершати вивчення певної теми, узагальнювати здобуті знання за допомогою простих таблиць і малюнків.
А комп’ютерний супровід дозволяє спростити для вчителя усвідомлення учнями завдань та вирішити проблему швидкого наочного зображення фігур, графіків, схем.
Усні вправи для 7 класу
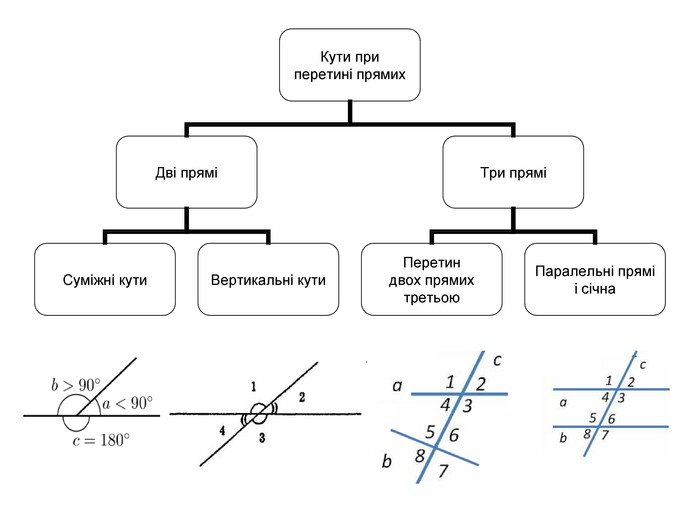
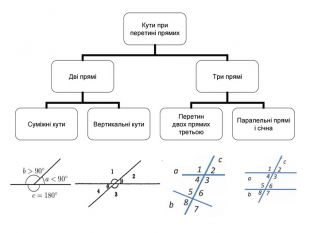
Суміжні кути та їх властивості
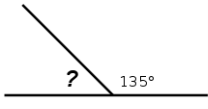
1. Знайдіть невідомий кут
2. Чи можуть два суміжні кути бути обидва:
а) гострими;
б) тупими;
в) прямими? Чому?
3. Величини суміжних кутів відносяться, як 4:5. Знайдіть ці кути.
4. Чи правильне твердження: Якщо один із суміжних кутів збільшити удвічі, то другий кут зменшиться у 2 рази?
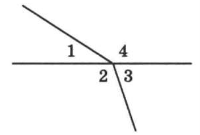
5. Чи є кути 3 і 4 суміжними? Чому?
Вертикальні кути та їх властивості
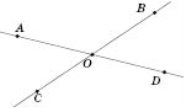
1. Чи утворились на малюнку вертикальні кути? Поясніть відповідь.
2. Величина кута 3 дорівнює 1200. Знайти ![]() 1 і
1 і ![]() 2.
2.
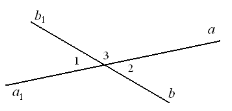
3. Один із кутів, утворених при перетині двох прямих, дорівнює 54°. Знайдіть решту кутів.
4. Сума двох вертикальних кутів дорівнює 80°. Знайдіть кожен із одержаних кутів при перетині прямих.
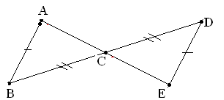
5. На малюнку зображені рівні трикутники. Вкажіть вертикальні кути, утворені за допомогою цих трикутників.
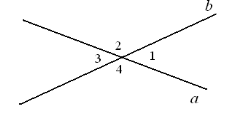
6. Будь-які два кути, що утворюються при перетині двох прямих, або суміжні, або вертикальні. Назвіть усі пари кутів і визначте їхній вид.
Усні вправи для 8 класу
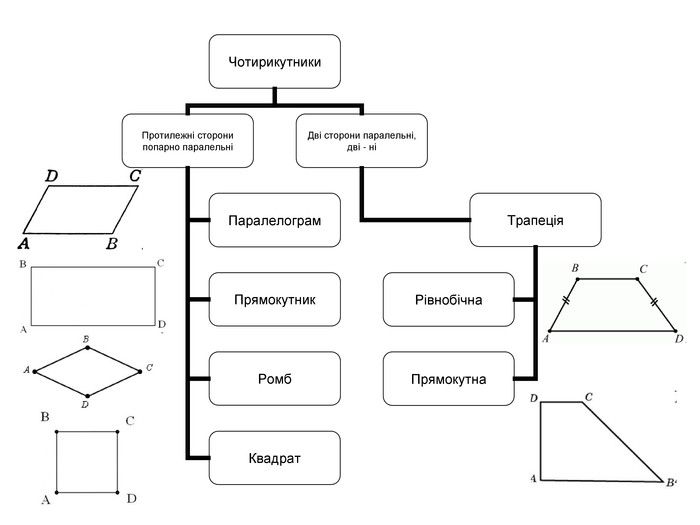
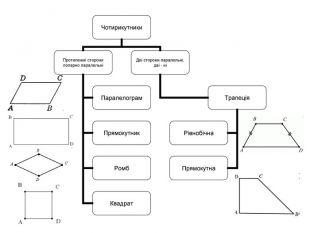
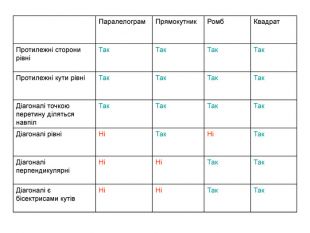
Паралелограм та його властивості. Ознаки паралелограма
1. Довжини сторін паралелограма відносяться, як 2:3, а його периметр дорівнює 20 см. Знайти сторони паралелограма.
2. Кут А паралелограма дорівнює 37. Знайдіть решту кутів паралелограма.
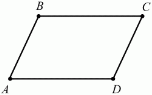
3. Сума двох кутів паралелограма дорівнює 74. Знайдіть решту кутів паралелограма.
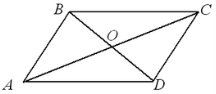
4. Один із кутів, утворених при перетині діагоналей паралелограма, дорівнює 43. Знайдіть кути паралелограма.
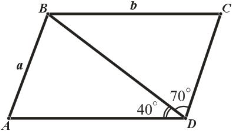
5. Знайдіть довжини сторін паралелограма.
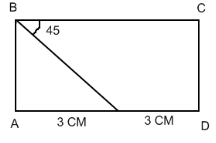
6. Знайдіть за малюнком кути паралелограма.
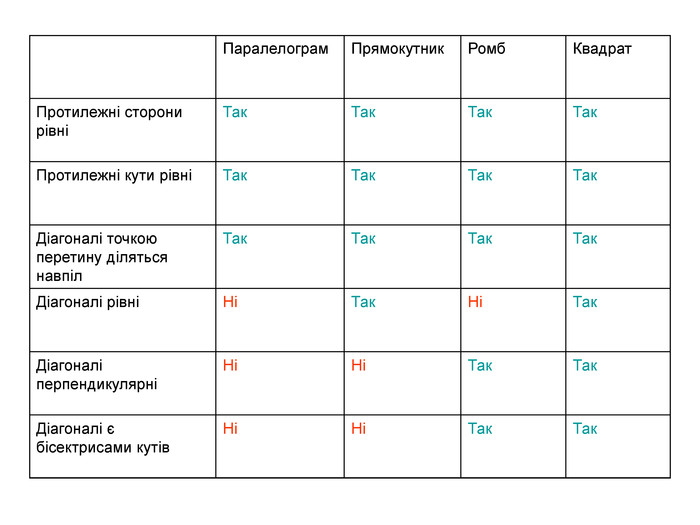
Прямокутник, ромб, квадрат та їх властивості
1. Діагональ ромба утворює зі стороною кут 25° . Знайдіть кути ромба.
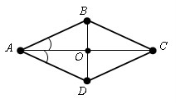
2. Периметр квадрата дорівнює 20 см. Знайдіть сторону квадрата.
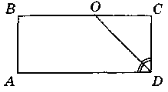
3. Бісектриса одного з кутів прямокутника ділить його сторону навпіл. Знайдіть довжини сторін прямокутника, якщо його периметр становить 30 см.
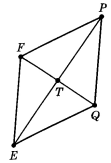
4. Кути, утворені діагоналями ромба з однією зі сторін, відносяться як 2:3. Знайдіть кути ромба.
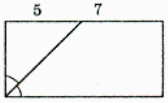
5. Периметр прямокутника дорівнює 96 см. Знайдіть його сторони, якщо вони відносяться як 1:3.
6. Знайдіть сторони прямокутника.
Трапеція
1. Знайдіть кути рівнобічної трапеції, якщо один із них дорівнює 70° .
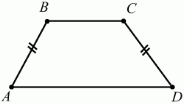
2. Знайдіть більшу основу трапеції
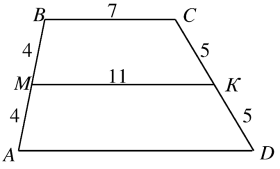
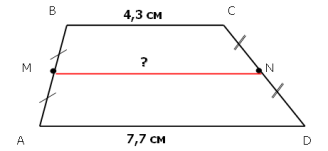
3. Знайдіть середню лінію трапеції
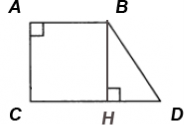
4. Основи прямокутної трапеції дорівнюють 4 см і 7 см, а один із кутів дорівнює 45° . Знайдіть висоту трапеції.
Вписані та центральні кути
1. Центральний кут дорівнює 120°. Знайдіть градусну міру вписаного кута, що спирається на ту саму дугу, що і центральний.

2. Вписаний кут дорівнює 45. Знайдіть міру відповідного йому центрального кута.
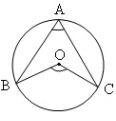
3. Центральний кут на 35° більший за вписаний кут, що спирається на ту саму дугу, що і центральний. Знайдіть градусні міри цих кутів.
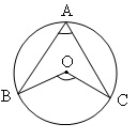
4. Сума градусних мір вписаного і центрального кутів дорівнює 135. Знайдіть ці градусні міри.
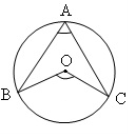
5. Як зміниться градусна міра центрального кута, якщо відповідний йому вписаний кут:
а) зменшити на 20;
б) збільшити у 3 рази?
Розв’язування прямокутних трикутників
1. Знайдіть довжину невідомої сторони трикутника.
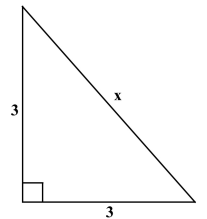
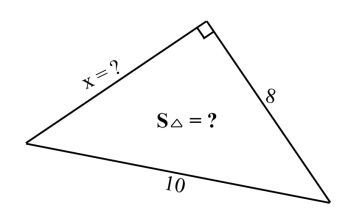
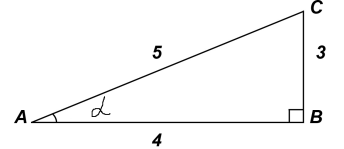
2. Знайдіть тригонометричні функції кута трикутника.
Усні вправи для 9 класу
Прямокутна система координат
1. У якій координатній чверті розміщена точка В (2; -5)?
2. Яка з точок має координати (-4; 3)? (5; -2)?
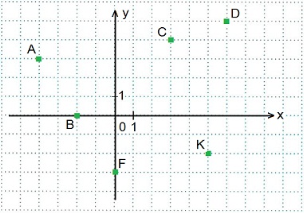
3. Яка з точок має абсцису -2?
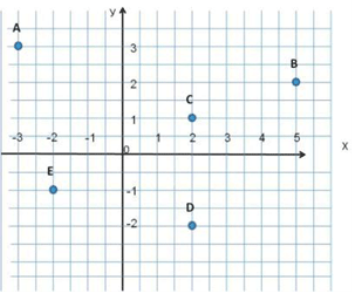
4. Яка з точок має ординату -2?
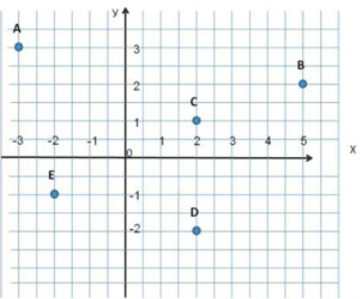
5. У якій координатній чверті розміщено центр кола, заданого рівнянням ![]() ?
?
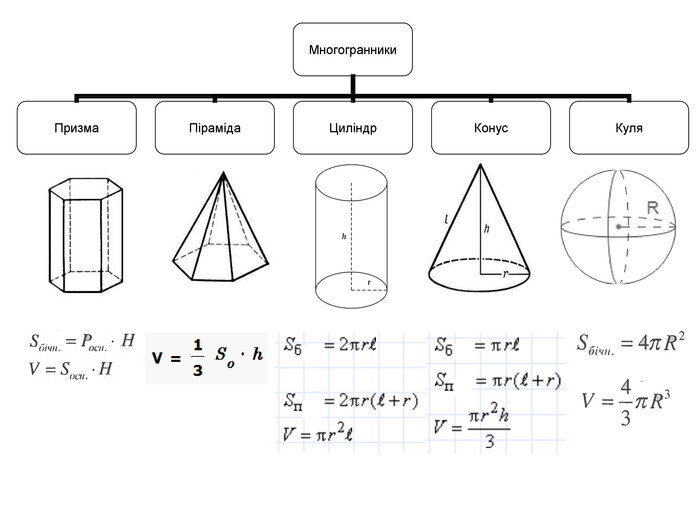
Формули для знаходження площі трикутника
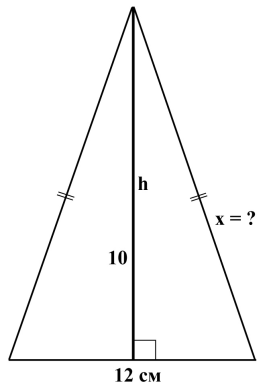
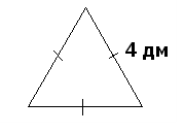
1. Знайти площу трикутників. S-?
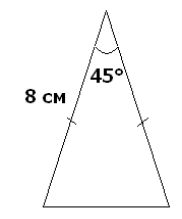
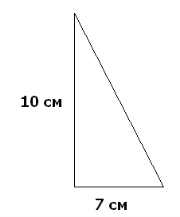
2. Бічна сторона й основа рівнобедреного трикутника відносяться як 5 : 6. Обчислити площу трикутника, якщо проведена до основи висота дорівнює
24 см.
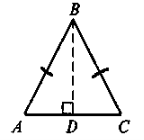
3. Знайти площу рівнобедреного трикутника, основа якого дорівнює 30 см, а периметр — 80 см.
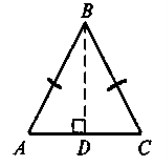
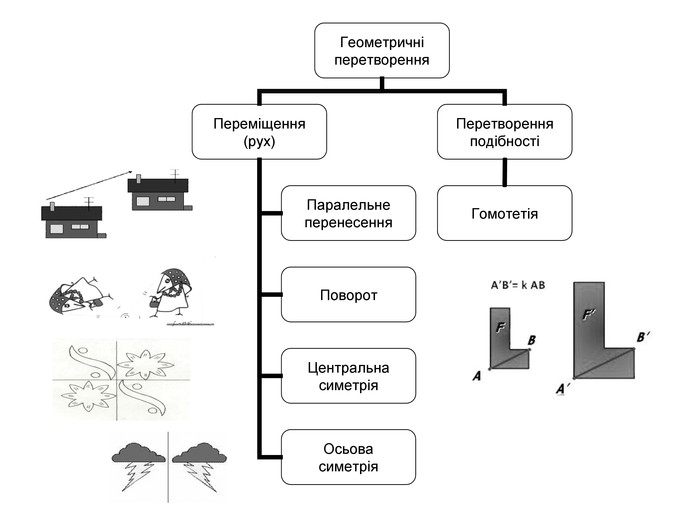
Геометричні перетворення
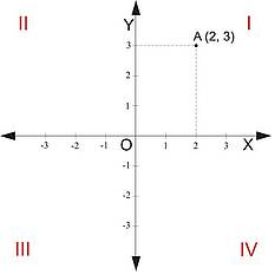
1. Вкажіть точки, симетричні точці А відносно осей координат та початку координат.
2. У яку точку переходить точка В(5; -7) при паралельному перенесенні, заданому формулами
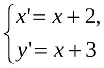
3. У яку точку перейде точка А(-2;3) в результаті паралельного перенесення вздовж осі ординат у додатному напрямі на 5 одиниць?
4. У яку координатну чверть переміститься фігура, розміщена в першій координатній чверті, при повороті на кут 90º проти годинникової стрілки навколо початку координат?
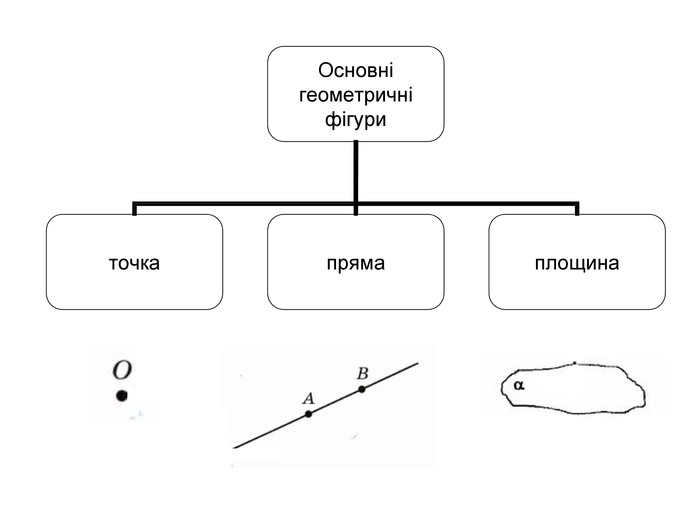
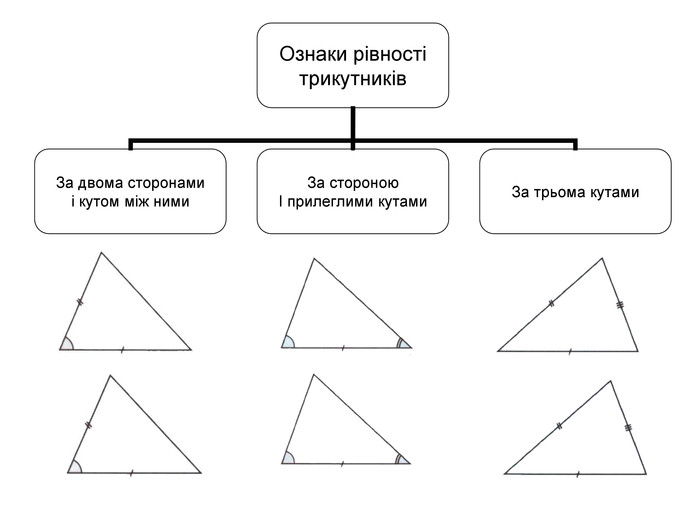
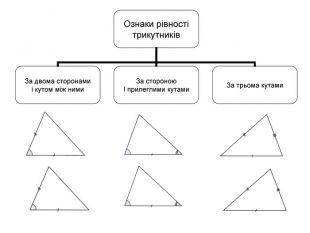
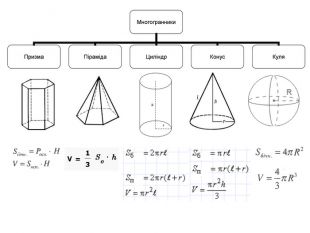
Схеми-узагальнення для 7 класу
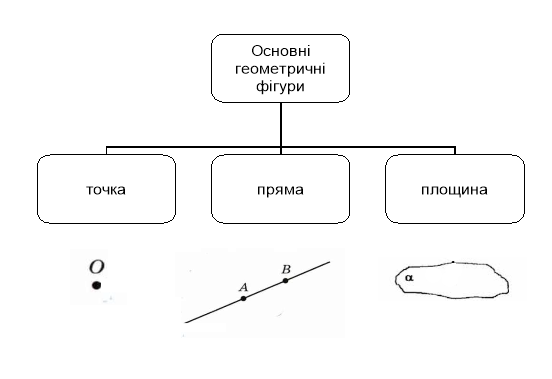
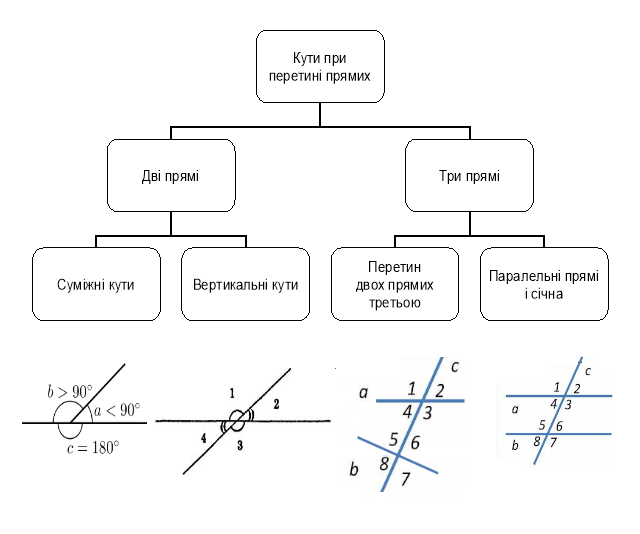
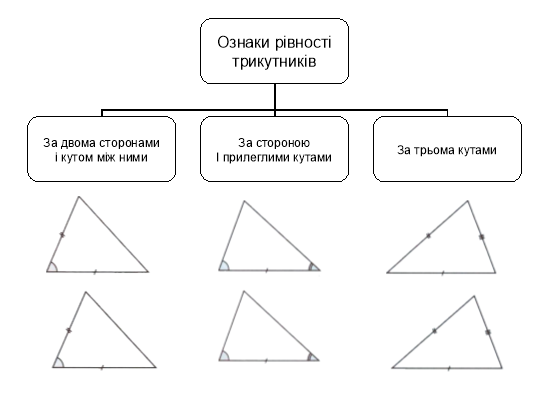
Схеми-узагальнення для 8 класу
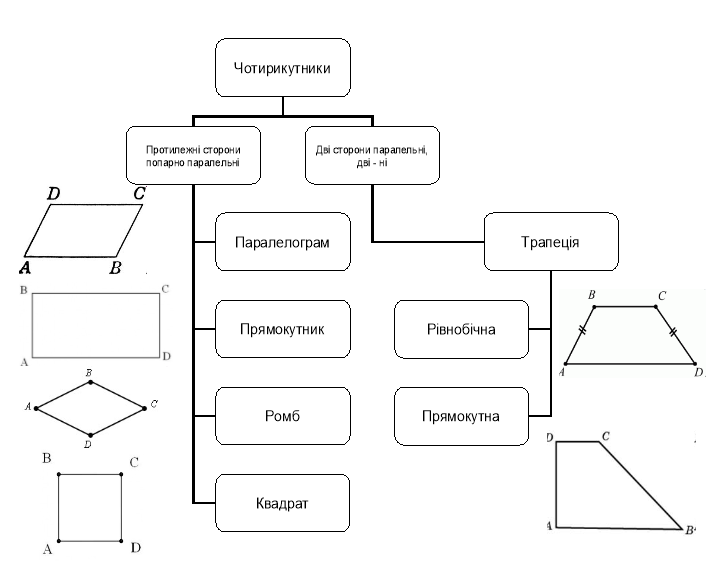
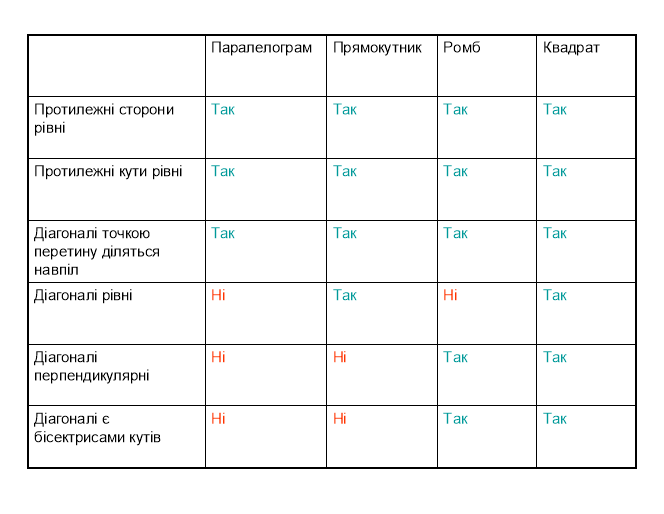
Схеми-узагальнення для 9 класу
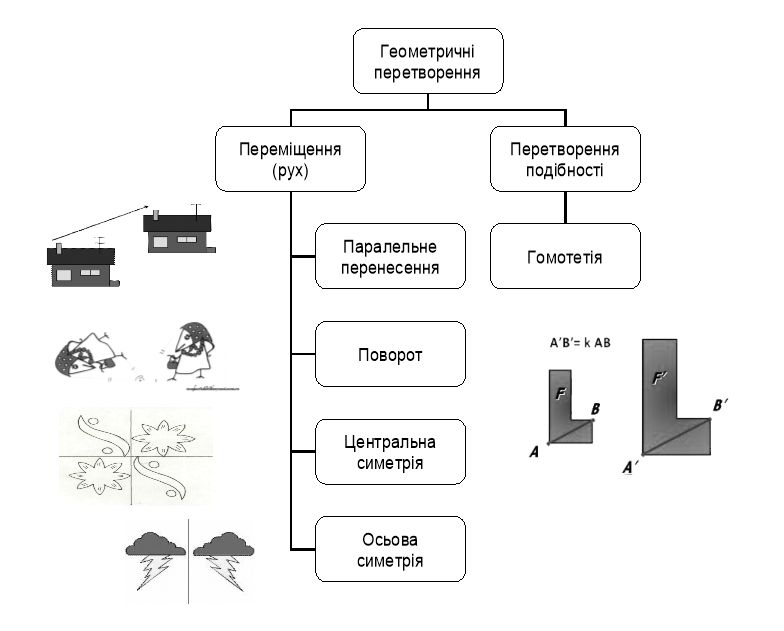
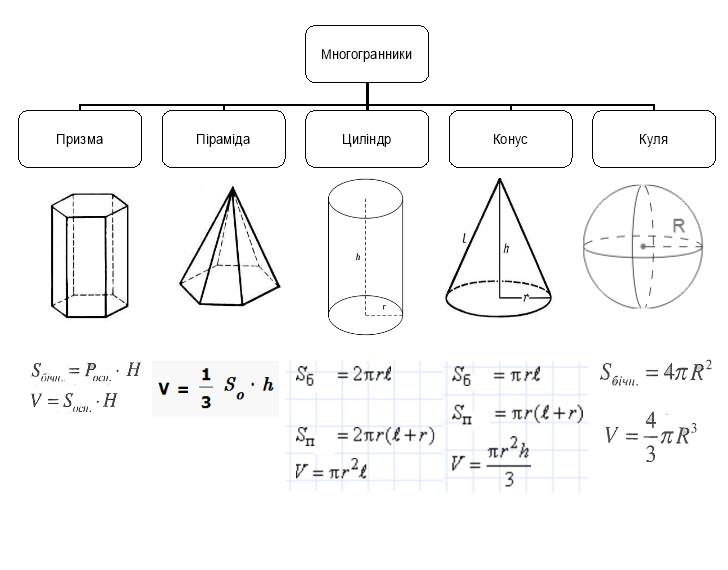
1


про публікацію авторської розробки
Додати розробку