Завдання до заліку по темі "Вектори"
Підбірку завдань з теми "Вектори, можно використовувати при підготовці до тематичної контрольної роботи або для проведення заліку з данної теми. Також ці завдання допоможуть учням підготуватися самостійно до узагальнюючого повторення теми.
ЗАВДАННЯ ДО ЗАЛІКУ З ТЕМИ
«ВЕКТОРИ»
-
Дано точки А(3;1) і В(-1;2). Знайдіть координати вектора АВ.
- На стороні СД паралелограма АВСД позначено точку М так, що СМ:МД=2:3. Виразіть
вектор АМ через вектори а і b, де а=АВ, b=АД.
-
Дано вектори а(3;-1) і b(1;-2). Знайдіть координати вектора m=3а-2b.
-
На рисунку зображено ромб АВСД, у якому АВ=2см, <АВС=1200. Знайдіть скалярний добуток векторів АВ і АС. В
А С
Д
-
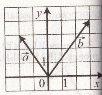
Знайдіть координати суми векторів а і b, зображених на рисунку
-
При якому значенні х вектори а (х;8) і b (3;9) перпендикулярні?
-
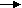
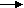На рисунку зображено квадрат АВСД. Який з векторів дорівнює АВ + ОД ?
В С
А Д
-
При якому значенні х вектори а (4;2) і b (х;-4) колінеарні ?
-
Відомо, що m = 3 p – 2 g. Знайдіть m , якщо p (1;-2), g (3;-1).
-
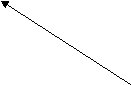
Відрізок ДЕ – середня лінія трикутника АВС, зображеного на рисунку. Яка з наведених рівностей правильна ? В
А). СВ = 2 ДЕ;
Б). СВ = - 2 ДЕ; Д
В). СВ = 0,5 ДЕ;
Г). СВ = - 0,5 ДЕ ? А
Е С
-
Обчисліть скалярний добуток ( а + 2 b )( а – b ), якщо а = b = 1, де <( а; b ) = 1200.
-
Знайдіть координати точки, яка є образом точки А (2; -3) при паралельному перенесенні на вектор а ( -1; 4 ).
-
На рисунку зображено паралелограм АВСД. Укажіть правильну рівність.
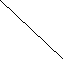
А). ВА + ВС = ВО; В С
Б). ВА + ВС = АС ;
В). ВА - ВС = АС;
Г). ВА – ВС = СА. А Д
14. Обчисліть модуль вектора а ( -1; 4).
15. На сторонах АВ і ВС паралелограма АВСД позначено відповідно точки М і К так, що АМ:МВ = 1:2, ВК:КС = 2:3. Виразіть вектор КМ через вектори АВ = а і АД = b.
16. При паралельному перенесенні на вектор а образом точки А ( -3; 7) є точка в (2;3). Які координати має образ точки С (1; - 5)при паралельному перенесенні на вектор а ?
17. Установіть вид кута між векторами а ( -3; 5) і b ( - 4; - 2).
18. На рисунку зображено паралелограм АВСД. Виразіть вектор АД через вектори ОД = а і ОС = b.
19. Обчисліть скалярний добуток векторів m (5; - 4) і n (2; 3).
20. Знайдіть кут між векторами а ( - 1; 1) і b ( 2; 0).
21. Дано точки А (- 1; 4), В ( 3; - 1), С (2; 2), Д ( 0;1). Укажіть правильну рівність.
А). АВ = СД; Б). АД = ВС; В). АС = ВД; Г). АС = ДВ.
22. Укажіть рисунок, на якому а + b – с = 0.
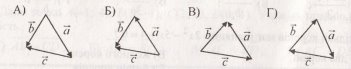
23. Укажіть рівняння кола, яке є образом кола х2 + y2 = 4 при паралельному перенесенні на вектор а ( 2; - 3).
А). (х – 2)2 + (y – 3)2 = 4; А). (х +2)2 + (y + 3)2 = 4;
Б). (х + 2)2 + (y – 3)2 = 4; А). (х – 2)2 + (y + 3)2 = 4;
24. При якому значенні n вектори а (n; 3) і b (-3; 3) перпендикулярні ?
25. Дано точки М (4; -2), N (1; 1) і Р (3; 3). Знайдіть М N . МР.
26. Знайдіть координати суми векторів АВ і ВС, якщо А (2; 4), С (3; - 2), В – деяка точка площини.
27. Дано точки М (4; -2) і К (2; 1). Знайдіть координати вектора МК.
28. На стороні АД паралелограма АВСД позначено точку К так, що АК:КД=1:2. Виразіть вектор ВК через вектори а і b, де а = АВ, b = АД.
29. Дано вектори а (-2; 1) і b (3; -1). Знайдіть координати вектора с = 2а - 3b.
30. На рисунку зображено ромб АВСД, у якому АВ=4 см, <ВАД = 600. Знайдіть скалярний добуток векторів ДВ і ДС. В
А С
Д
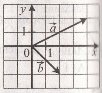
31. Знайдіть координати різниці а – b вектора, зображеного на рисунку.
32. При якому значенні у вектори а (2; -4) і b (6; у) перпендикулярні?
33. На рисунку зображено квадрат АВСД. Який з векторів дорівнює різниці АО - ВС?
В С
А Д
34. При якому значенні у вектори а (2; 5) і b (-6; у) колінеарні ?
35. Відомо, що с = 2а - 3b. Знайдіть с , якщо а (-1; 1) і b (-2; 3).
36. Відрізок МК – середня лінія трикутника АВС, зображеного на рисунку. Виразіть вектор КМ через вектор АС. В
К М
А С
37. Сторона правильного шестикутника АВСДЕF дорівнює 1. Обчисліть скалярний добуток АД . СД.
38. Обчисліть скалярний добуток ( а - 2 b)(а + b), якщо а = 
39. Знайдіть координати точки, яка є образом точки В (4; -5) при паралельному перенесенні на вектор с (-3; 7).
40. На рисунку зображено паралелограм АВСД. Укажіть правильну рівність.
А). СВ + СД = ВД; В С
Б). СВ + СД = СА;
В). СВ + СД = СО; А Д
Г). СВ – СД = ВД.
41. Обчисліть модуль вектора а (-2; 3).
42. На сторонах ВС і СД паралелограма АВСД позначено відповідно точки Е і М так, що ВЕ:ЕС=3:4, СМ:МД=1:3. Виразіть вектор ЕМ через вектори АВ = а і АД = b.
43. Визначте вид чотирикутника АВСД, якщо вектори ВС і АД колінеарні і ВС = АД.
44. При паралельному перенесенні на вектор а образом точки М (1; -2) є точка К (-2; 5). Які координати має образ точки Р (0; -3) при паралельному перенесенні на вектор а?
45. Установіть вид кута між векторами m ( -8; 3) і n ( 2; 5).
46 . На рисунку зображено паралелограм АВСД. Виразіть вектор АВ через вектори СО = а і ДО = b.
В С
А Д
47. Обчисліть скалярний добуток векторів а ( -7; 9) і b ( -2; -1).
48. Знайдіть кут між векторами а ( -2; 2
49. Дано точки А(-4;1), В(-2;4), С(2;5), Д(0;2). Укажіть правильну рівність.
А). АВ=СД; Б). СВ=АД; В). СВ=ДА; Г). АВ=АД.
50. Укажіть рисунок, на якому а + b + с = 0.
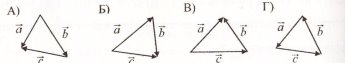
51. Укажіть рівняння кола, яке є образом кола х2 + у2 = 4 при паралельному перенесенні на вектор а (-5; -4).
А). (х +5)2 + (y – 4)2 = 4; А). (х - 5)2 + (y + 4)2 = 4;
Б). (х - 5)2 + (y – 4)2 = 4; А). (х + 5)2 + (y + 4)2 = 4;
52. При якому значенні а вектори m (4; а) і n (- 5; 2) перпендикулярні?
53. При якому значенні n вектори а (n; 3) і b (- 3; 3) перпендикулярні?
54. Знайдіть координати різниці векторів АВ і АС, якщо В (5; 7), С (- 1; 4), А – деяка точка площини.
про публікацію авторської розробки
Додати розробку