Розробка уроку з алгебри на тему ВИРАЗИ ЗІ ЗМІННИМИ

Урок №14.

ВИРАЗИ ЗІ ЗМІННИМИ

Мета: вдосконалити вміння учнів працювати з виразами, що містять змінні (обчислення значень виразів, знаходження ОДЗ виразів зі змінними).

Тип уроку: застосування вмінь.

Хід уроку

І. Перевірка домашнього завдання

Особливо ретельно слід перевірити виконання завдання № 2 (на складання виразу зі змінними) та № 3 (на знаходження ОДЗ змінної у виразі).

№ 2. Вираз має вигляд: . Якщо , , то

(к).

Відповідь. На 80 к.

№ 3. Для учнів досить складним є момент переходу від умови, за якої вираз не має змісту (дільник або знаменник дорівнюють нулю), до умови, коли вираз має зміст (тобто з множини будь-яких чисел виключаємо ті значення змінної, при яких вираз не має змісту):

1) має зміст при будь-яких значеннях , бо це — цілий вираз;

2) має зміст при всіх , окрім 0;

3) має зміст при всіх , окрім , бо при ;

4) має зміст при будь-яких значеннях , бо це — цілий вираз.

ІІ. Актуалізація опорних знань

Замість рутинного (і не досить ефективного) фронтального опитування можна організувати роботу в парах (або групах) із таким завданням.

Дано вирази: ; ; .

Порівняйте їх і знайдіть якомога більше відмінностей.

Під час презентації результатів виконання роботи, учні відтворюють зміст основних понять теми:

1. Числові вирази і виразі зі змінними.

2. Значення числових виразів та виразів зі змінними.

3. Вирази, що не мають змісту.

ІІІ. Удосконалення вмінь

На цьому уроці продовжуємо роботу з удосконалення вмінь учнів:

а) обчислювати значення виразів зі змінними;

б) знаходити значення змінних, при яких вираз має зміст;

в) складати вирази за певними умовами.

Рівень завдань підбираємо більш високий.

Виконання письмових вправ

1. Знайдіть значення виразу , якщо:

1) ; ; 2) ; ; 3) ; ; 4) ; .

2. Відомо, що ; . Знайдіть значення виразу:

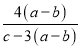1) ; 2) ; 3) ; 4) .

3. При яких значеннях змінної має зміст вираз:

1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ?

 Оскільки учні ще не володіють умінням розв’язувати рівняння розкладанням многочленів на множники, розв’язувати дробові рівняння, системи рівнянь, завдання розв’язуємо із використанням міркувань приблизно такого змісту: оскільки змінна в знаменнику виразу (вираз дробовий), то, щоб вираз мав зміст, необхідно, щоб знаменник не дорівнював 0. Але оскільки не може бути від’ємним числом, то сума не може дорівнювати 0 при жодних значеннях , тому не дорівнює 0 ні при яких значеннях . Отже, вираз має зміст при будь-яких (і т. д.).

4. Складіть вираз для розв’язування задачі.

а) Периметр прямокутника 16 см, одна з його сторін см. Яка площа прямокутника?

б) З двох міст, відстань між яким км, назустріч одне одному виїхали два автомобілі. Швидкість одного з них км/год, а швидкість другого — км/год. Через скільки години вони зустрінуться?

5. Запишіть у вигляді виразу:

1) суму добутку чисел і і числа ;

2) різницю числа і частки чисел і ;

3) добуток різниці чисел і та їх суми;

4) частку суми і та їх різниці.

IV. Діагностика засвоєння

Самостійна робота (різнорівнева)

1. Знайдіть значення виразу:

А. , якщо . (2 б.) Б. , якщо . (3 б.)

В. , якщо , . (4 б.)

2. Складіть вираз, що відповідає умові:

А. Різниця чисел та . (2 б.)

Б. Піврізниця добутку чисел –0,2 та та числа 0,8. (3 б.)

В. Швидкість човна в стоячій воді дорівнює км/год. Швидкість течії річки км/год. За який час човен подолає км за течію річки? (4 б.)

3. Знайдіть, при яких значеннях змінної має зміст вираз:

А. . (2б) Б. . (3 б.) В. . (4 б.)

Під час виконання роботи учні повинні вибрати тільки одне завдання (А, Б, В) з трьох запропонованих. Оцінюємо відповідно: А — 2 бали, Б — 3 бали; В — 4 бали. (Учень має право вибирати завдання різного рівня, наприклад № 1 — А, № 2 — В, № 3 — Б.)

V. Рефлексія

Перевіряємо правильність виконання завдань. (Учні отримують таблицю із розв’язаннями й відповідями та перевіряють свої роботи.)

VI. Домашнє завдання

№ 1. Випереджальне

Дано вирази:

1) та . Порівняйте значення цих виразів при та ; ; . Що ви помітили?

2) та . Порівняйте значення цих виразів при ; ; . Що ви помітили?

Як ваші міркування записати мовою математики?

3) та . Порівняйте значення цих виразів при . Що ви помітили? Чи будуть виконуватися для виразів та ті ж самі властивості, що й для двох попередніх пар виразів? Який висновок можна зробити?

№ 2. При яких значеннях змінної має зміст вираз:

1) ; 2) ; 3) ; 4) ?