Розробка уроку з алгебри на тему "Властивості функції."

Тема уроку. Властивості функції.

Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів викону­вати дії для знаходження названих властивостей функцій. За допомогою вивчених означень та вироблених умінь дослідити відомі учням елементарні функції на предмет проміжків зростання та спадання.

Тип уроку:  закріплення знань та вмінь.

Наочність та обладнання: опорний конспект № 13.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Перевірку виконання письмових вправ можна, як і на попе­редньому уроці, провести у формі само- або взаємоперевірки за зразком.

Засвоєння теоретичного матеріалу попереднього уроку можна перевірити під час фронтальної бесіди або виконання тестових за­вдань (див. нижче).

Тестові завдання

1. Функція y = f(x) зростаюча, якщо:

а) х₂ > х₁;     б) у₂ > у₁;

в) при х₂ > х₁ f(x₂) < f(x₁);   г) при х₂ > х₁ f(x₂) > f(x₁).

2. Функція y = f(x) спадна, якщо:

а) х₂ < х₁;     б) f(x₂) < f(x_l);

в) при х₂ < х₁ f(x₂) < f(x_l);   г) при х₂ > х₁ f(x₂) < f(x₁).

3. Якщо відомо, що f(3) = 0, то:

а) х = 3 є нулем функції у = f(x); б) у = 3 є нулем функції y = f(x);

в) х = 0 — це нуль функції у = f(x); г) функція y = f(x) має нулі.

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Після перевірки виконання домашнього завдання (як письмо­вих вправ, так і усної його частини) та корекції можливих помилок учні усвідомлюють необхідність подальшої роботи із закріплення як знань, так і вмінь, які були сформовані на попередньому уроці.

Крім того вчитель може спрямувати увагу учнів на питання про дослідження відомих їм із курсу 7 і 8 класів функцій на предмет проміжків зростання й спадання та інших властивостей. Таким чи­ном, учитель виділяє два основні напрямки роботи учнів на уроці, тобто формулює основні завдання на урок:

1. закріпити знання та вміння, набуті учнями на попередньому уроці;
2. за допомогою цих знань та вмінь дослідити елементарні функ­ції, відомі учням, та зафіксувати отримані висновки у вигляді опорних тверджень.

IV. Закріплення знань

Усні вправи

1. Розв'яжіть рівняння:

1) х² – 3х + 2 = 0;  2) 3x – 1 = 0; 3) kx + b = 0 k 0 (відносно х).

2. Розв'яжіть нерівність:

1) 5 – х ≥ 0;          2) 1 – 3x < 0; 3) 2х – 3 > 2x – 5;         4) -х + 3 < -х – 1.

3. У яких проміжках f(x) < 0, якщо:

1) f(x) = 1 – 2x;  2) f(x) = 4x – 2?

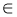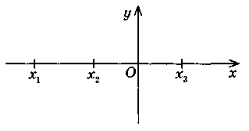
4. Відомо, що х₁, х₂, х₃ — нулі функції f(x), причому f(x) > 0 на проміжках (х₁, х₂) і (х₃; +∞); і f(x) < 0, якщо х (-∞; х₁) і х 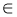(х₂; х₃). Як виконати ескіз графіка (див. рисунок), якщо функція має графіком безперервну лінію?

Методичний коментар

Під час розв'язування учнями усних вправ слід вимагати від них аргументованих відповідей (тобто пояснень із посиланням на відповідне означення, а також точного відтворення цього озна­чення).

V. Закріплення знань

Письмові вправи

Зміст вправ, які планується розв'язати на даному уроці, майже такий самий, що і зміст вправ попереднього уроку:

1. знайти нулі, проміжки знакосталості, проміжки зростання та проміжки спадання деякої функції, заданої графічно;
2. за допомогою обчислень знайти нулі функції, заданої форму­лою y = f(x);
3. за допомогою обчислень визначити, зростає чи спадає дана функція на заданому проміжку.

Проте до названих вправ додаємо вправи на дослідження еле­ментарних функцій (лінійної, оберненої пропорційності, квадра­тичної функції та функції   у = ), знайомих учням із 7 та 8 класів, на зростання та спадання, а також на проміжки знакосталості. Результати цих досліджень слід зафіксувати як опорні факти і за­кріпити ці факти на усних та письмових вправах.

До названих вправ бажано додати вправи на повторення ма­теріалу попередніх уроків — на відшукання області визначення функції, заданої формулою y = f(x), і на відпрацювання навичок роботи з поняттям графіка функції та оперативних умінь роботи з формулою y = f(x).

VI. Підсумки уроку

Контрольні запитання

1. Яка з даних функцій є спадною (спадає на кожному проміжку своєї області визначення)?

1) у = 2;  2) у = ;   3) у = -2х;   4) у = .

2. Яка з даних функцій додатна на проміжку (2; +∞)?
   1) у = 2;  2) у = х – 2;  3) у = -х + 2;  4) у = .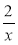

VII. Домашнє завдання

1. Вивчити зміст означень, розглянутих на попередньому уроці, та виділені на цьому уроці властивості елементарних функцій.
2. Розв'язати вправи на застосування вивчених означень та фактів.
3. Повторити зміст поняття «графік функції».