Розробка уроку геометрії для 7 класу на тему "Сума кутів трикутника. Зовнішній кут трикутника" за підручником Г. П. Бевз, Геометрія для 7 класу, "Генеза", 2015 року

 

                                        (Дистанційне навчання)

                                              Геометрія, 7 клас

 

Вчитель математики

Каплунівської гімназії

Бабич Юлія Іванівна

 

24 листопада 2023 року ( урок № 23).

(Підручник Геометрія Г. П. Бевз,  видавництво «Генеза», 2015 рік – 192 с.)

 

Мета уроку: засвоїти теорему про суму кутів трикутника, поняття зовнішнього кута трикутника; формувати вміння застосовувати теорему під час розв’язування задач; розвивати логічне мислення та практичні навички учнів; виховувати самостійність, активність, відповідальне ставлення до навчання, інтерес до геометрії.

Тип уроку: засвоєння нових знань.

Освітнє середовище: креслярські інструменти, підручник, гаджет, онлайн-дошка Jamboard, слайди, тести.

 

                                                 ХІД УРОКУ.

І. Організаційний момент.

ІІ. Повідомлення теми і мети уроку. Мотивація учнів: що ви знаєте про кути трикутника? Замислювалися ви над тим, чи може бути в трикутнику два прямих кути,  прямий  і тупий, два тупих? Чи хотілося б дізнатися відповіді на ці запитання?

ІІІ. Актуалізація опорних знань.

• Трикутник – це фігура, утворена трьома точками, що не лежать на одній прямій, та трьома … (відрізками, які сполучають ці точки).
• Кожний трикутник має три вершини і три … (сторони).
• Суми довжин всіх сторін трикутника називають… (периметром).
• Кожна сторона трикутника коротша за … (суму двох інших його сторін).
• Кожний трикутник має три медіани, … (три висоти і три бісектриси).
• За кутами трикутники є гострокутні, … (прямокутні, тупокутні).
• За сторонами трикутники є рівносторонні, … (рівнобедрені, різносторонні)
• Трикутники зустрічаються всюди – в різних архітектурних спорудах, …

 

IV. Засвоєння нових знань.

   

                             План вивчення нового матеріалу.

 

1. Теорема про суму кутів трикутника та наслідок з неї.

                                                  Доведення:

 

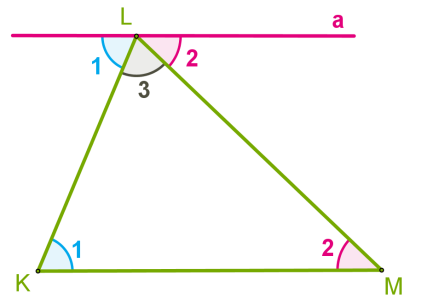
Розглянемо довільний трикутник KLM і доведемо, що  ∠K+ ∠L + ∠M= 180°.

 

1. Проведемо через вершину L пряму a, паралельну стороні KM.

2. Кути, позначені цифрою 1, є внутрішніми різносторонніми кутами при перетині паралельних прямих a і KM січною KL.

 3. Кути, позначені цифрою 2, — є внутрішніми різносторонніми кутами при перетині тих самих паралельних прямих січною ML.

  4. Очевидно, що сума кутів 1, 2 і 3 дорівнює розгорнутому куту з вершиною L, тобто:

∠ 1+ ∠ 2 + ∠ 3= 180°  або  ∠ K+ ∠ L + ∠ M= 180°   Теорему доведено.

  

 Висновок 1. Сума гострих кутів прямокутного трикутника дорівнює 90°.

 Висновок 2. У рівнобедреному прямокутному трикутнику кожен гострий кут дорівнює 45°.

 Висновок  3. У будь-якому трикутнику або всі кути гострі, або два кути гострі, а третій тупий або прямий.

 

2. Теорема про зовнішній кут трикутника та наслідок з неї.

 

Зовнішнім кутом трикутника називається кут, суміжний із внутрішнім кутом даного трикутника.

 

Теорема (про зовнішній кут трикутника):
Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.

 

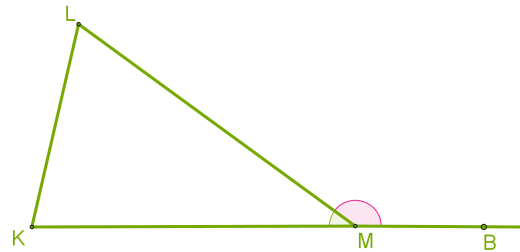
                                                 Доведення:

 

Із рівностей  ∠ KML + ∠ BML = 180°   і  ∠ K+ ∠ L + ∠ KML= 180° 

 отримуємо, що: ∠ BML= ∠ K + ∠ L

 Наслідок: Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.

 

Чи можуть бути в трикутнику:

• Два прямі кути;
• Кути 100° та 120°;
• Два тупі кути;
• Один прямий, інший тупий?

 

V. Первинне усвідомлення нового матеріалу.

 

1. Знайдіть невідомий кут трикутника, якщо два його кути 65° та 45°.

180° – (65° + 45°) = 70°

 

2. Знайдіть кути, якщо їхні градусні міри відносяться як 1:3:5.

х+3х+5х=180°       

9х=180°                 3∙20°=60° – кут 2.

х=180°:9                5∙20°=100°– кут 3.

х=20° – кут 1.       Відповідь: 20°, 60°, 100°.

 

3. Знайдіть кути трикутника, якщо один із них 80°, інший удвічі менший.

         

1.     80°:2=40°
2.     180° – (80° + 40°) = 60°

Відповідь: 40° і 60°.

 

              Самостійна робота учнів.

                   Вправа 1: скільки трикутників на малюнку?

 

 

Відповідь: 5

                                      

                                

 

 

 

                                     Вправа 2.

 

                                                Вправа 3.

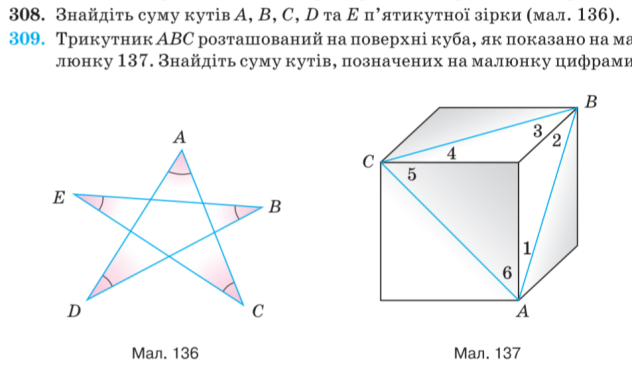
VI. Підсумок уроку. Чому навчилися на уроці?

Учень: на уроці ми набули навички та вміння застосовувати теорему про суму кутів трикутника та теорему про властивість зовнішнього кута трикутника до розв´язування задач.

 

VIІ. Оцінювання учнів.

VIІI. Домашнє завдання:

§ 10, вивчити правила, стор. 76-78, вправа 295, 298.