Розробка уроку з теми "Прогресії"

 

Тема: Прогресії

 

Дидактична мета:  повторити,узагальнити, систематизувати, розшири-                                      

                              ти і поглибити знання, отримані при вивченні те-

                              ми « Прогресії».

Виховна мета:  виховувати наполегливість, вміння трудитися, самос-

                        тійність, відповідальність.        

Розвиваюча мета:  розвивати культуру математичних записів, науко-

                             вий світогляд, зацікавленість предметом, матема-

                             тичну  інтуїцію, логічне мислення учнів.

Обладнання: реферати ( « Історична  довідка  про  поняття  прогресії»,

                       «Легенди, пов’язані  з  прогресіями», «Де  ми  зустрічаємось  з     

                      прогресіями в житті?», «Підбірка  задач з розв’язаннями  на  за-

                     стосування прогресій (практичних та таких, що містять міжпре-

                   дуетні зв’язки)»), роздатковий матеріал, екран, проектор.

 

Хід уроку

    1.  Реферат: « Історична довідка про поняття прогресії».

    В наш час числові послідовності розглядаються як окремі випадки функцій. Числова послідовність є функція натурального аргументу. Так, наприклад, арифметична прогресія є лінійною функцією натурального аргументу, а геометрична - показниковою функцією натурального аргументу.

    Прогресії - окремі випадки числових послідовностей - зустрічаються в пам’ятках ІІ тисячоліття до н. е.

    В клинописних табличках вавілонян, як і в єгипетських папірусах, що відносяться до ІІ тисячоліття до н. е. зустрічаються приклади арифметичних та геометричних прогресій.

    Ось єгипетська задача з папіруса Ахласа.

    «Нехай тобі сказано: розділи 10 мір ячменю між 10 чоловіками, різниця ж між кожним чоловіком дорівнює міри».

    При розв’язанні цієї та інших аналогічних задач єгиптяни, очевидно, користувалися правилом, яке можна записати в сучасній символіці і еквівалентне нашій формулі: = .                                                            

    Задачі на арифметичні та геометричні прогресії є і в давньокитайському трактаті  «Математика в дев’яти книгах”.

    Перші з задач на прогресії, які дійшли до нас, пов’язані з потребами господарського життя та суспільної практики, як, наприклад, розподіл продуктів, поділ спадщини і т. д.

    З однієї клинописної таблички можна зробити висновок, що спостерігаючи за Луною від новолуння до повнолуння, вавілоняни помітили: в перші 5 днів після новолуння збільшення освітлення лунного диску здійснюється за законом геометричної прогресії зі знаменником 2. Розв’язання і відповідь, подані  в таблиці, наводять на думку, що автор задачі користувався формулою S _n  = 2ⁿ + ( 2ⁿ ─ 1 ), однак про те, як він дійшов до неї, ми нічого поки не знаємо.

    В давньоросійському юридичному збірнику «Русская правда» є викладки про приплід від скота та бджіл за відомий проміжок часу, про кількість зерна, зібраного з певної частини землі …

    Ці задачі, очевидно, не мали господарського або юридичного значення, а як і в інших країнах були результатом розвитку інтересів любителів математики до математичного змісту подібних задач; однак вперше задачі на прогресії виникли із спостережень над явищами природи та з дослідницьких суспільно-економічних явищ, до яких можна застосувати закони арифметичної та геометричної прогресій.

    Слово «прогресія» латинського походження, буквально означає «рух вперед» і зустрічається вперше у римського автора Боеція ( V - VІ ст.)

    (Всі учні класу оцінюють усні виступи своїх товаришів). У цей час на дошці готуються відповіді на запитання:

    а)  послідовності;

    б)  означення арифметичної прогресії, формула n - го члена арифметичної прогресії;

    в)  означення геометричної прогресії, формула n - го члена геометричної прогресії; ( один з учнів пояснює аналогію у виводі формули );

    г)  показ розв’язання задач, завчасно підібраних, на застосування формули n - го члена геометричної прогресії:

    1)  b₁ = 4;    q = ;    b₅ = ?

    2)  b₄ = ─ 54;    q = 3;    b₁ =?

    3)  c₃ = ─ ;    c₅  = ;    q = ?

    Всі відповіді, записані на дошці, оцінюють визвані учні.

 

2.  Легенди, пов’язані з прогресіями.

    ( Оскільки суть легенди а) викладена в підручнику, то можна зупинитися тільки на наступному):

    а)  Про шахову дошку.

    Індійський цар не міг виконати обіцяну нагороду «Не в твоїй владі, повелитель, виконувати подібні бажання. В усіх амбрах твоїх немає такої кількості зерен, яке вимагає Сета. Немає його і в житницях цілого царства. Не знайдеться такої кількості зерен і на  всьому земному просторі.  І якщо бажаєш обов’язково видати обіцяну нагороду, то накажи перетворити земні царства в піхотні поля, накажи висушити моря і океани, накажи розтопити льоди і сніги, що вкривають далекі північні пустелі. Нехай весь простір їх буде засіяно пшеницею. І все те, що вродить на цих полях, накажи віддати Сеті. Тоді  він отримає свою винагороду.

    З подивом слухав цар слова старця.

    - Назви мені це жахливе число, - сказав він у роздумах.

    - 18 квінтильйонів 446 квадрильйонів  744 трильйона 73 більйона 709 мільйонів 551 тисяча 615 повелитель.

 

     б)  Легенда  «Нагорода»

    Ось що, за легендою, відбулося багато століть назад в Стародавньому Римі.

    Полководець Теренцій, за наказом імператора, здійснив переможний похід і з трофеями повернувся в Рим. Після повернення в столицю він звернувся з проханням допустити його до імператора. Імператор ласкаво зустрів полководця, сердечно подякував йому за військові заслуги імперії і обіцяв в нагороду дати високе положення в сенаті.

    Але Теренцію потрібно було не це. Він заперечив:

‒ Багато перемог одержав я, щоб зміцнити твою могутність, государ, і овіяти ім’я твоє славою. Я не боявся смерті, і будь у мене не одне, а багато життів, я всі їх приніс би тобі в жертву. Але я зморився воювати; минула молодість, кров повільно біжить в моїх жилах. Настала пора відпочити в будинку моїх пращурів та насолодитися радощами домашнього життя.

 ‒ Чого хотів би ти від мене, Теренцій? - запитав імператор.

‒ Я бідний, государ … Якщо хочеш подарувати нагороду скромному слузі твоєму, - сказав Теренцій, - то нехай щедрість твоя допоможе мені дожити мирно в достатку роки біля домашнього вогнища. Государ, дай мені грошей для забезпечення залишка мого життя.

    Імператор - говорить легенда - не відрізнявся щедрістю. Він любив накопичувати гроші для себе і скупо витрачав їх на інших. Прохання полководця змусило його задуматися.

‒ Яку ж суму, Теренцій, вважав би ти для себе достатньою? - запитав він.

‒ Мільйон динаріїв, государ.

    Знову задумався імператор. Нарешті імператор заговорив:

‒ Доблесний Теренцій! Ти великий воїн, а славетні подвиги твої заслужили щедрої винагороди. Я дам тобі багатство. Завтра опівдні ти почуєш тут моє рішення.

    Теренцій поклонився і вийшов.

    Наступного дня імператор сказав Теренцію:

‒ Не хочу, щоб такий благородний воїн, як ти, отримав за свої подвиги жалку винагороду. Вислухай же мене. У моєму казначействі лежать 5 мільйонів мідних брасів. Ти ввійдеш в казначейство, візьмеш одну монету в руки, повернешся сюди і покладеш її до моїх ніг. Наступного дня знову підеш в казначейство, візьмеш монету, що дорівнює 2 брасам і покладеш тут поряд з першою. Третього дня принесеш монету вартістю 4 браси, 4-го дна - монету вартістю  8 брасів і т. д. Будеш щоразу подвоювати вартість монет. Я накажу щодня виготовляти для тебе монети відповідної цінності. І доки вистачить у тебе сил піднімати монети, ти будеш виносити їх з мого казначейства.

    Теренцій уважно вислухав імператора. Йому ввижалася величезна купа монет, одна більша іншої, які він винесе з державного казначейства.

‒ Я задоволений твоєю щедрістю і милістю, государ, - відповів він з радісною посмішкою. - Воістину щедра винагорода твоя!

    Почалися щоденні відвідини Теренцієм державного казначейства. Перші походи з монетами не коштували Теренцію ніяких зусиль.

    В перший день він виніс з казначейства всього один брас. Це невелика монета, 21 мм в діаметрі і 5 г вагою. Легкими були також другий, третій, четвертий, п’ятий та шостий переходи. Сьома монета важила в наших сучасних мірах 320 г і мала діаметр 84 мм. На 8 - й день Теренцію прийшлось винести з казначейства монету, яка відповідала 128 одиничним монетам. Вона важила 640 г і була діаметром близько 10,5 см. На 9-й день Теренцій приніс монету в 256 од. монет. Вона мала діаметр 13 см і важила більше 1,25 кг. 13-го дна Теренцій приніс монету, яка дорівнювала 4096 од. монетам, діаметром 34 см і вагою 20,5 кг. На 16-й день полководець хитався під ношею, що лежала на його спині. Ця монета, рівна 32 768 од. монетам, важила 164 кг. 18-й день був останнім днем збагачення Теренція. Йому довелося доставити цього разу монету, що відповідала 131 072 од. монетам з діаметром більше 1 м і вагою 655 кг. Користуючись своїм списом як ричагом, Теренцій з неймовірними зусиллями ледве закотив її в залу. З гуркотом впала монета до ніг імператора. Теренцій був зовсім  змучений.

    ‒ Не можу більше … Досить , - прошепотів він.

    Імператор ледве стримував сміх задоволення, коли бачив повний успіх своєї хитрості. Він наказав казначеєві порахувати, скільки всього брасів вніс Теренцій в приймальну залу. Вийшло 262 143 браси.

    Отже, скупий імператор дав полководцю близько 20-ї частини тої суми в мільйон динаріїв, яку просив Теренцій.

 

3.  В цей час на дошці 4 учні відповідають на такі питання:

а)  показ (ілюстрація) розв’язання задач, підібраних раніше, на використання формули n-го члена арифметичної прогресії:

    1)  а₄ = 7;    а₁ = ─ 2;    d - ?

    2)  а₅ = 0;    d = ─ 1;    а₁ - ?

    3)  а₁ = 8;    d =  ─ 4;    а₁₈ - ?    а_k -?

б)  властивості членів арифметичної прогресії;

в)  властивості членів скінченої геометричної прогресії;

г)  задача. Відомо, що середньорічний відсоток приросту виробництва тканин приблизно 9,1 %. Дізнатися,  скільки відсотків буде приріст виробництва тканин через три роки?

4.  На дошці виводять:

    а)  формулу n-го члена арифметичної прогресії;

    б)  формулу суми n перших членів арифметичної прогресії;

    в)  формулу суми n перших членів геометричної прогресії;

    г)  формулу суми нескінченної геометричної прогресії при │q│< 1.

5.  Реферати:

    а)  Де ми зустрічаємося з прогресіями в житті.

    Прогресії - не абстрактне поняття. З ними ми зустрічаємося в житті і при вивченні різних явищ.

    Прикладами арифметичних прогресій є:

    1)  вартість проїзду в таксі в залежності від зміни відстані на 1 км;

    2)  вартість телеграми в залежності від кількості слів;

    3)  залежність суми внутрішніх кутів опуклого многокутника від числа сторін n ;

    4)  вік учнів в залежності від класу, в якому вони навчаються (при умові щорічного переходу з класу в клас);

    5)  швидкість рівномірного руху (v = v₀ + at ) в залежності від часу t;

    6)  лінійне розширення тіла ( l = l₀ ( 1 + at )) в залежності від часу t та ін.

    Прикладами величин, що змінюються в геометричній прогресії є:

    1)  зміна в кінці кожного року величини грошової суми вкладника, що поклав свої гроші до банку;

    2)  концентрація розчиненої речовини в розчині при переході з одного горизонтального шару до іншого, які віддалені один від одного на однакову відстань;

    3)  сила F, необхідна для утримання ваги Р за допомогою каната, намотаного на барабан в залежності від кута обхвату барабана;

    4)  зміна тиску атмосфери зі знаменником 9,8826, якщо зміна висоти підняття над рівнем моря відбувається в арифметичній прогресії, різниця якої дорівнює 1 км;

    5)  швидкість хімічної реакції в залежності від температури;

    6)  ланцюгова незатухаюча реакція ділення ядра урану 235.

 

б)  Задачі практичного змісту на прогресії.

    1)  Щоб заасфальтувати частину дороги довжиною 117 м, використовують два катки. Перший каток встановили на одному кінці ділянки, другий - на протилежному. Працювати вони почали одночасно. За першу хвилину перший каток пройшов 1 м, за кожну наступну він проходив на 0,5 м більше, ніж за попередню. Другий каток за кожну хвилину проходив 6 м. Через скільки хвилин обидва катки зустрінуться?

Розв’язання

    Нехай обидва катки зустрінуться через х хв.. Тоді другий каток до зустрічі пройде відстань 6х м, а перший - пройде відстань, що дорівнює сумі членів арифметичної прогресії, де а₁ = 1,   n = х, d = .

= = = = .

    Весь шлях дорівнює 117 м. Складемо рівняння: 6х +  = 117;

 

+ 27х ─ 468 = 0;

D = 729 + 1872 = 2601;

= 12;  0     - корінь не задовольняє умову задачі.

 

     2)  Два тіла падають на землю, причому падіння першого тіла почалося на 2 сек. раніше, ніж другого. За першу секунду тіло пролетіло 4,9м, а за кожну наступну секунду швидкість його падіння збільшується на 9,8 м  (опором повітря знехтувати).Через скільки секунд після початку падіння першого тіла відстань між тілами буде дорівнювати 1000 м?

Розв’язання

    Нехай відстань між двома тілами через х сек. після початку падіння першого тіла дорівнює 1000 м.

    Тоді шлях S₁, пройдений першим тілом за х сек., буде сумою членів арифметичної прогресії, у якої а₁ = 4,9,  d = 9,8,  а число членів х.

    Нехай шлях S₂, пройдений другим тілом, дорівнює сумі членів арифметичної прогресії, у якої а₁ = 4,9,  d = 9,8,  а число членів х =2.

    За умовою задачі S₁ ─ S₂ = 1000.

    = = = 4,9;

= = = 4,9.

 

    Таким чином 4,9 х² ─ 4,9 ( х ─ 2 )² = 1000,

    4,9 х² ─ 4,9 х² + 19,6 х ─ 19,6 = 1000;

    19,6 х = 1019,6;

    x = 52.

   Відповідь: 52сек..

    3)  Кількості тонн вугілля, яке добувається кожною з трьох шахт за добу, утворюють зростаючу геометричну прогресію, сума якої 3780. Із добутого другою та третьою шахтами вугілля відправили, відповідно, 600 і 1740 т, після чого кількості вугілля почали утворювати арифметичну прогресію. Знайти кількість вугілля, здобутого за добу на кожній з шахт.

Розв’язання

    Нехай кількості тонн вугілля, видобутого кожною шахтою за добу, утворюють зростаючу геометричну прогресію:b₁, b₂, b₃. За умовою задачі сума членів цієї прогресії дорівнює 3780, тобто b₁ + b₁ q + b₁ q² = 3780 або

b₁ ( 1 + q + q² ) = 3780.

    Після відправлення вугілля з другої та третьої шахт, кількості тонн вугілля на кожній з них стали утворювати арифметичну прогресію b₁,

b₁q ─ 600,  b₁q ² ─ 1740, сума членів якої дорівнює  ( 3780 ─ ( 600 + 1740 )=

= 1440, тобто   = 1440.                                

    Складаємо систему рівнянь:

b₁ ( 1 + q + q² ) = 3780,                         b₁ ( 1 + q + q² ) = 3780,                  

(b₁ ( 1 + q² ) ─ 1740) ∙ 3 = 1440;            b₁ ( 1 + q² ) = 960 + 1740;

                  2

 

 

   b₁ ( 1 + q + q² ) = 3780,       b₁ = 2700;       2700 ( 1 + q + q² ) = 3780;

   b₁ ( 1 + q² ) = 2700;                    1+q²                       1 + q²

 

5 ( 1 + q + q² ) = 7 ( 1 + q²);

5 + 5q +5q² = 7 + 7q²;

2q² ─ 5q + 2 = 0;

D = 25 ─ 16 = 9;

q₁ = = 2;     q₂ = = .

За умовою задачі геометрична прогресія b₁,  b₂,  b₃ зростаюча, отже q>1, a q= не задовольняє умову задачі, тобто q = 2.

   b₁ = = = 540.

   b₂ = b₁ ∙ q = 540 ∙ 2 = 1080;

   b₃ = b₁ ∙ q² = b₂ ∙ q = 1080 ∙ 2 = 2160.

    Відповідь: 540 т, 1080 т, 2160 т.

 

в)  Розв’язування задач на прогресії:

    1)  По конвейєру рухаються 10 деталей, вздовж конвейєра розташований ряд робочих місць. На першому робочому місці знімається 3 деталі, а на кожному наступному на 2 деталі більше, ніж на попередньому місці. Крім того, на кожне робоче місце конвейєра поступає додатково 13 деталей. Яка найбільша кількість деталей може бути на конвейєрі і на якому робочому місці?

Розв’язання

    Припустимо, що найбільша кількість деталей на конвейєрі буде на х-му місці. Тоді на робочих місцях з конвейєра буде знято  деталей, а поступить 13х деталей. Загальна кількість деталей, що поступили на конвеєр, на х-му місці буде наступною:                                                           

 

    = 10 + 13x ‒ = ‒ + 11x + 10 = ‒ + .

 

                                                    

      S(x) = - + = 40  при х= 5;  6.

    Найбільша кількість деталей на конвеєрі на 5 і 6 робочих місцях буде 40 штук.

    2)  знайти суму + + + … +  ,

 

якщо а₁, а₂ ,…, а_n  утворюють арифметичну прогресію.

Розв’язання

 

    ( ‒ + ‒ + … + ‒ ) =   ( ‒ ).

 

    3)   + + + + .

Розв’язання

- + - + - + - + - = - = .

 

    4)  Нестандартна задача.

    Дана сума: 2⁸  + 2⁷  + 2⁶  + 2⁵ + 2⁴  + 2³ + 2²  + 2 +1.Чи можна, закреслюючи ті чи інші доданки, отримати будь - яке натуральне число від 1 до 511 включно? Знайти алгоритм, за допомогою якого це можна зробити, якщо він існує.

Розв’язання

    405 = 2⁸ + 149,

                       149 = 2⁷ + 21,

                                         21 = 2⁴ + 5,

                                                         5 = 2² + 1.

405 = 2⁸  + 2⁷  + 2⁴  +2² + 1.

Аналогічно: 57 = 2⁵ + 2⁴  + 2³  + 1. Всі обчислення спрощуються, якщо користуватися таблицею степенів числа 2.

    5)  Софізм. Захисники релігії старалися використовувати поняття  нескінченної геометричної прогресії для «доведення» існування бога. Так, італійський математик Гранді в 1710 році надрукував роботу, в якій на основі математичних досліджень «довів», що бог міг створити видимий світ з нічого. Робив він це так. Позначимо

S = 1 - 1 + 1 - … + ( -1)ⁿ⁺¹ + …

Тоді S - 1 = - 1 + 1 - 1 + … + ( -1)ⁿ⁺¹ + … = - S,   2S = 1,   S = .

З іншого боку, S = ( 1 - 1 ) + (1 - 1) + (1 - 1) + … = 0 + 0+ 0+ … = 0.

Таким чином, S = і S = 0, а тому = 0, а ця рівність і символізує акт створення богом матеріального світу з нічого.

    Гранді неправомірно використовує сполучний закон додавання для нескінченної множини доданків, бо він справджується тільки в використанні для скінченої множини доданків.

    6)  Геометрична ілюстрація трійки чисел, що утворюють відповідно арифметичну та геометричну прогресію

 

                             D

 A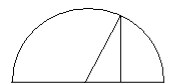B

                 О     С

а )  AC;       OD;          CB.             б)     AC;          CD;         CB.

      a;             ;           b.                     a                              b

 

7.  Самостійна  робота у трьох варіантах (за бажанням) на

10 хвилин.

Варіант А

1)  В арифметичній прогресії (а_n ) перший член дорівнює 8, різниця дорівнює ─4. Знайти а₁₈ ;  а _k;  S₁₈  .

2)  В арифметичній прогресії  (а_n) a ₁₀ = 23,  a₁ = 5.Знайти різницю.

3)  Перший член геометричної прогресії (х_n ) дорівнює 6, знаменник дорівнює . Знайти суму перших шести її членів та х_k .

 

Варіант В

1)  Знайти різницю арифметичної прогресії (а_n ), якщо а₁ = 28,  а₂₁ = 4.

2)  Який номер члена арифметичної прогресії (х_n ), що дорівнює 17,2, якщо  х₁ = 5,3  і різниця дорівнює 0,7.

3)  Послідовність (b_n ) -геометрична прогресія. Виразити b₁₂ через b₇ та знаменник прогресії.

4)  Послідовність (у_n ) - геометрична прогресія, причому   

                                                                               

    =9,

                                                                                                                                                                      

      + = 540.                                                                                             

 

 

Знайти у₁.

5)  Знайти суму шести членів геометричної прогресії, якщо b₁ = 3, а знаменник дорівнює 2.

 

Варіант С

1)  Довести, що якщо числа ;  ;  утворюють арифметичну прогресію, то числа а² , b² , с²  також утворюють арифметичну прогресію.

2)  Між числами   та 240 вставити шість таких чисел, які разом з даними числами утворюють геометричну прогресію.

3)  В правильний трикутник, сторона якого а, вписане коло; в нього вписаний правильний трикутник; в цей трикутник знову вписане коло і т. д. Знайти суму периметрів трикутників.

 

8.  Підсумки уроку.

Література

1. Г. П. Бевз, В. Г. Бевз  « Алгебра, 9 клас» (Видавництво: ВД Освіта).

2.  І. В. Александрова « Математичні терміни».-М. «Вища школа»,1978.    

3.  Г. І. Гейзер «Історія математики в школі 7 - 8 класи».- М.,1982.

 4.  Г. М. Возняк, К. П. Маланюк «Прикладна спрямованість шкільного курсу

    математики».- К, 1984.

5.  Ф. А. Бартенєв « Нестандартні задачі з алгебри».-М., 1976.

6.  І. М. Кіпнік « Задачі на складання рівнянь і нерівностей ».-М.,1980.

7.  Я. І. Перельман «Жива математика».- М., 1978.