Розробка занять для математичного онлайн - гуртка на тему "Математична індукція"
Відповіді до д.з.№1
№1. Розглянемо квадратний тричлен ![]() і обчислимо значення многочлена при
і обчислимо значення многочлена при ![]() дістанемо :
дістанемо :
![]()
Легко помітити, що всі ці числа прості. Підставляючи ![]() , ми ще довго діставатимемо прості числа . Тому природно висловити гіпотезу, що значення
, ми ще довго діставатимемо прості числа . Тому природно висловити гіпотезу, що значення ![]() при всіх натуральних
при всіх натуральних ![]() є простими. Але ця гіпотеза є неправильною, оскільки, якщо
є простими. Але ця гіпотеза є неправильною, оскільки, якщо ![]() , ми дістанемо,
, ми дістанемо, ![]() , тобто
, тобто ![]() - складене число.
- складене число.
№2. Для зручності запису позначимо
![]() .
.
- При n=1 рівність виконується:
![]() , тобто 2=2.
, тобто 2=2.
-
Припускаємо, що задана рівність правильна при n=k, де
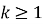 , тобто
, тобто
![]() . (1)
. (1)
- Доведемо, що рівність виконується і при n=k+1, тобто доведемо, що
![]() .
.
Враховуючи, що ![]() , і підставляючи
, і підставляючи ![]() з рівності (1), одержуємо
з рівності (1), одержуємо ![]() , що й потрібно було довести.
, що й потрібно було довести.
- Отже, задана рівність правильна для будь-якого натурального n.
№1. Доведення
1)Якщо ![]() , то маємо
, то маємо ![]()
2) Припустимо, що коли ![]() вираз
вираз ![]() і доведемо, що вираз кратний 27, якщо
і доведемо, що вираз кратний 27, якщо ![]()
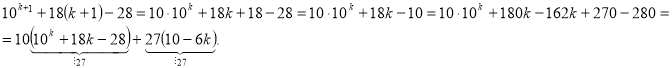 Отже,
Отже, ![]() .
.
Дане твердження істинне для всіх ![]()
№2. Доведення
1)Якщо ![]() , то маємо
, то маємо ![]()
2) Припустимо, що коли ![]() :
: ![]() ,
,
тобто ![]() і розглянемо вираз , коли
і розглянемо вираз , коли ![]() .
.
Отримаємо : ![]()
Виконаємо перетворення :
 За принципом математичної індукції , істинність твердження доведена для всіх натуральних
За принципом математичної індукції , істинність твердження доведена для всіх натуральних ![]() .
.
№1. Довести, що ![]() , при
, при ![]()
Доведення
1) ![]()
2) ![]()
Доведемо твердження для ![]() :
:
![]()
![]()
![]()
![]()
№2. Довести, що значення виразу ![]() кратне 7.
кратне 7.
Доведення
1) Якщо ![]() , то маємо
, то маємо ![]()
2) Припустимо, що коли ![]() вираз
вираз ![]() і доведемо , що вираз кратний 7 при
і доведемо , що вираз кратний 7 при ![]() Для доведення достатньо показати, що різниця кратна 7, тобто
Для доведення достатньо показати, що різниця кратна 7, тобто
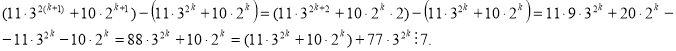 Оскільки за припущенням
Оскільки за припущенням ![]() і
і ![]()
Отже, твердження, що доводиться, є правильним.
Дане твердження можна було довести іншим способом.
![]()
Оскільки вираз![]() кратний 7 для будь – якого натурального
кратний 7 для будь – якого натурального ![]() і вираз
і вираз ![]() , то і весь вираз кратний 7.
, то і весь вираз кратний 7.
Відповіді до д.з. №4
№1. Методом математичної індукції доведіть нерівність:
![]()
Доведення
![]()
![]()
![]()
![]()
![]()
Припустимо, що нерівність виконується при ![]() :
:
![]()
![]()
![]()
![]()
![]()
Помножимо нерівність 2) на 2 і перенесемо всі змінні вліво:
![]()
До нерівності 3) додамо та віднімемо ![]() , і перенесемо всі змінні вліво:
, і перенесемо всі змінні вліво:
![]()
що і потрібно було довести.
(Вираз ![]()
![]()
![]()
оскільки за умовою ![]() а
а ![]()
(оскільки дана функція завжди додатна).
№2. Доведіть нерівність за допомогою методу математичної індукції
![]() якщо
якщо ![]()
Доведення
![]()
припустимо що нерівність виконується при n=k:
![]()
![]()
![]()
помножимо нерівність 2) на 4, отримуємо:
![]()
щоб отримати подібний вираз, додамо та віднімемо від нерівності 3)
вираз ![]()
![]()
що і потрібно було довести (вираз ![]() за припущенням, а
за припущенням, а
![]() оскільки k>1).
оскільки k>1).
Відповіді до д.з. №5
№1. Довести, що сума внутрішніх кутів опуклого многокутника обчислюється за формулою ![]() , де
, де ![]() - кількість кутів многокутника.
- кількість кутів многокутника.
Доведення
1) При ![]() утвориться трикутник , а така теорема про суму кутів трикутника відома.
утвориться трикутник , а така теорема про суму кутів трикутника відома. ![]() .
.
2) Припустимо, що сума кутів ![]() - кутника обчислюється за формулою
- кутника обчислюється за формулою ![]() . Добавимо ще одну вершину , утвориться
. Добавимо ще одну вершину , утвориться ![]() - кутник. Тоді сума його внутрішніх кутів дорівнює сумі кутів
- кутник. Тоді сума його внутрішніх кутів дорівнює сумі кутів ![]() - кутника та кутів трикутника, тобто
- кутника та кутів трикутника, тобто ![]()
![]()
За принципом математичної індукції дане твердження справедливе для будь – якого ![]() - кутника.
- кутника.
№2. Довести, що ![]() різних точок , що належать одній прямій, розбивають її на
різних точок , що належать одній прямій, розбивають її на ![]() інтервал ( з яких два є нескінченними)
інтервал ( з яких два є нескінченними)
Доведення
1) Якщо ![]() , то дане твердження є істинним , оскільки одна точка поділяє пряму на 1+1=2 інтервали.
, то дане твердження є істинним , оскільки одна точка поділяє пряму на 1+1=2 інтервали.
2) Припустимо, що дане твердження істинне , коли ![]() ( тобто
( тобто ![]() різних точок розбивають пряму на (
різних точок розбивають пряму на (![]() ) інтервал).
) інтервал).
Далі довільно виберемо на прямій ![]() точку:
точку: ![]() . Якщо відкинути одну точку
. Якщо відкинути одну точку ![]() , то залишиться
, то залишиться ![]() точок, що поділяють пряму на (
точок, що поділяють пряму на (![]() ) інтервал. Точка
) інтервал. Точка ![]() належить одному з цих інтервалів і поділяє його на два інтервали. Тому загальна кількість інтервалів, на які поділяють пряму (
належить одному з цих інтервалів і поділяє його на два інтервали. Тому загальна кількість інтервалів, на які поділяють пряму (![]() ) точка дорівнює
) точка дорівнює ![]() .
.
Отже, твердження істинне , коли ![]() , а з його істинності , коли
, а з його істинності , коли ![]() , випливає його істинність і коли
, випливає його істинність і коли ![]() . За принципом математичної індукції, воно істинне для всіх натуральних
. За принципом математичної індукції, воно істинне для всіх натуральних ![]() .
.
Домашня робота №1
Завдання 1. Розгляньте тричлен ![]() і знайдіть його значення при x=1;2;3;4;5. Зробіть припущення. Встановіть, чи є висловлена гіпотеза правильною.
і знайдіть його значення при x=1;2;3;4;5. Зробіть припущення. Встановіть, чи є висловлена гіпотеза правильною.
(Спростувати гіпотезу можна контрприкладом)
Завдання 2. Довести , що![]()
Завдання 1. Довести, що ![]() кратне 27,
кратне 27, ![]()
Завдання 2. Довести, що вираз ![]() ділиться на 133,
ділиться на 133, ![]()
Домашня робота №1
Завдання 1. Довести, що ![]() , при
, при ![]()
Завдання 2. Довести, що значення виразу ![]() кратне 7.
кратне 7.
Завдання 1. Методом математичної індукції доведіть нерівність:
![]()
Завдання 2. Доведіть нерівність за допомогою методу математичної індукції
![]() якщо
якщо ![]()
Домашня робота №5
Завдання 1. Довести, що сума внутрішніх кутів опуклого многокутника обчислюється за формулою ![]() , де
, де ![]() - кількість кутів многокутника.
- кількість кутів многокутника.
Завдання 2. Довести, що ![]() різних точок , що належать одній прямій, розбивають її на
різних точок , що належать одній прямій, розбивають її на ![]() інтервал ( з яких два є нескінченними)
інтервал ( з яких два є нескінченними)
Заняття 1
Суть методу математичної індукції
Слово індукція означає перехід від окремих тверджень до загальних. Наприклад, числа 20, 50, 110, 170 діляться на 2. Тому всі числа, що закінчуються нулем, діляться на 2.
Але індукція може привести і до неправильного висновку.
Виникає питання: якщо твердження справедливе в кількох окремих випадках, то як дізнатися, чи справедливе воно взагалі. На це питання інколи вдається відповісти за допомогою так званого методу математичної індукції.
Методом математичної індукції є одним з універсальних методів доведення математичних тверджень, особливо тих у яких містяться слова «для довільного натурального n» (можливо сформульовані неявно).
Доведення методом математичної індукції проводиться так. Спочатку твердження перевіряють при ![]() . Цю частину доведення називають базою індукції. Якщо при
. Цю частину доведення називають базою індукції. Якщо при ![]() твердження істинне, то переходять до другої частини доведення , що називають індуктивним кроком або індуктивним переходом. У цій частині доводять справедливість твердження для
твердження істинне, то переходять до другої частини доведення , що називають індуктивним кроком або індуктивним переходом. У цій частині доводять справедливість твердження для ![]() , допускаючи істинність твердження , коли
, допускаючи істинність твердження , коли ![]() .
.
Опорна схема
-
Перевіряємо істинність твердження при

-
Припускаємо істинність твердження при
 та доводимо, спираючись на припущення, істинність твердження при
та доводимо, спираючись на припущення, істинність твердження при 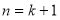 .
.
-
Робимо висновок про істинність твердження для будь- якого натурального
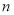 .
.
Приклад 1. Обчислити суму ![]() перших непарних натуральних чисел.
перших непарних натуральних чисел.
Розв’язання.
Будемо спостерігати як «поводиться» сума ![]() перших непарних чисел. Маємо:
перших непарних чисел. Маємо:
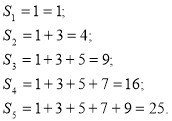
Числа 1; 4; 9; 16; 25 є квадратами послідовних натуральних чисел.
Тепер можна зробити припущення, що для будь – якого натурального ![]() :
: ![]()
Доведемо цей факт методом математичної індукції.
1) База індукції. Перевіряємо істинність твердження при ![]() .
.
![]() .
.
2) Індуктивний перехід .Припустимо, що дане твердження істинне при ![]() , тобто твердження :
, тобто твердження : ![]() - справедливе.
- справедливе.
Доведемо, що дана рівність справедлива і коли ![]() , тобто є правильною рівність:
, тобто є правильною рівність: ![]()
Розглянемо ліву частину
![]()
Але за припущенням індукції , сума ![]() .
.
Отже, вся сума дорівнює ![]()
За принципом математичної індукції , істинність твердження доведено для будь – якого ![]() .
.
Приклад 2. Довести, що для будь – якого натурального ![]() виконується рівність
виконується рівність
![]()
Розв’язання. Доведемо її методом математичної індукції.
1) Якщо ![]() , то
, то ![]()
Дана формула справедлива при ![]()
2) Припустимо, що формула справедлива при ![]() , тобто
, тобто ![]() і доведемо істинність при
і доведемо істинність при ![]() .
.
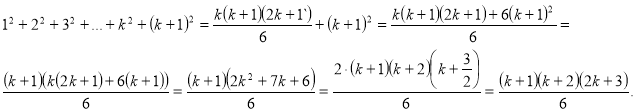 Отже, твердження істинне при
Отже, твердження істинне при ![]() , а з його істинності при
, а з його істинності при ![]() , випливає його істинність при
, випливає його істинність при ![]() . За принципом математичної індукції, припущення істинне при всіх натуральних
. За принципом математичної індукції, припущення істинне при всіх натуральних ![]() .
.
Заняття 2
Доведення подільності виразів
На занятті ми розглянемо, ще одну сферу застосування методу математичної індукції – доведення подільності виразів. Адже ознаки подільності не завжди дозволяють довести подільність виразів на те чи інше число, на той чи інший вираз. І тут на допомогу може прийти метод математичної індукції.
Приклад 1. Довести, що ![]() кратне 7,
кратне 7, ![]()
Доведення
1) Якщо ![]() , то маємо:
, то маємо: ![]()
2) Припустимо, що коли ![]() вираз
вираз ![]() і доведемо , що вираз кратний 7 при
і доведемо , що вираз кратний 7 при ![]() .
.
![]()
Отже, ![]() Твердження доведено для всіх
Твердження доведено для всіх ![]()
Приклад 2. Довести, що числа виду ![]() кратні 9,
кратні 9, ![]()
Доведення
1) Якщо ![]() , то маємо :
, то маємо : ![]()
2) Припустимо, що коли ![]() вираз
вираз ![]() і доведемо, що коли
і доведемо, що коли ![]() вираз теж кратний 9.
вираз теж кратний 9.
![]()
Отже, ![]() Дане твердження справедливе для всіх
Дане твердження справедливе для всіх ![]()
Приклад 3. Довести, що ![]() при будь – якому натуральному
при будь – якому натуральному ![]() ділиться на 6 без остачі.
ділиться на 6 без остачі.
Доведення
1) Якщо ![]() , то число
, то число ![]() ділиться на 6.
ділиться на 6.
2) Припустимо, що коли ![]() вираз
вираз ![]() ділиться на 6 та доведемо , то даний вираз ділиться на 6, якщо
ділиться на 6 та доведемо , то даний вираз ділиться на 6, якщо ![]() .
.
![]() .
.
Обидва доданки діляться на 6 без остачі : перший містить число 120, яке кратне 6, а другий ділиться на 6 без остачі згідно припущення.
За принципом математичної індукції , істинність твердження доведена для всіх натуральних ![]() .
.
Зауваження .Дане твердження можна було довести без використання методу математичної індукції.
![]()
Даний добуток ділиться на 6, оскільки один з множників![]() ділиться на 6 без остачі.
ділиться на 6 без остачі.
Заняття 3
Доведення подільності виразів (продовження)
Приклад 1. Доведіть, що n3- n ділиться на 3 при будь-якому натуральному значенні n.
Доведення
Нам потрібно показати, що вираз n3–n при довільному натуральному n ділиться на 3.
При n = 1, n3–n =0 ділиться на 3.
Перевіряємо справедливість цього твердження при n=2.
При n = 2 n3–n = 8 - 2 = 6, тобто твердження справедливе.
Припустимо тепер, що вираз k3 – k ділиться на 3.
Тоді при n = k + 1 одержуємо:
(k+1)3- k-1= k3 + 3k2 + 3k + 1 – k – 1 = k3 + 3k2 + 3k – k = k3– k + 3(k2 + k).
Вираз k3 – k ділиться на 3 по припущенню. Вираз 3(k2 + k) теж ділиться на 3. Тому, і вся сума k3– k + 3(k2 + k) також ділиться на 3. Таким чином доведено, що вираз n3–n ділиться на 3 при довільному n.
Приклад 2. Довести, що ![]() ділиться на 6 для всіх натуральних
ділиться на 6 для всіх натуральних ![]() .
.
Доведення
Доведемо, що вираз ![]() ділиться на 6 для всіх натуральних
ділиться на 6 для всіх натуральних ![]() .
.
1) Якщо ![]() , то маємо
, то маємо ![]() , тобто вираз , даний в умові , є числом цілим.
, тобто вираз , даний в умові , є числом цілим.
2) Припустимо, що коли ![]() , вираз
, вираз ![]() ділиться на 6, тобто
ділиться на 6, тобто ![]() і доведемо, що
і доведемо, що ![]() також ділиться на 6. Перетворимо цей вираз:
також ділиться на 6. Перетворимо цей вираз:
![]() Отриманий добуток обов’язково кратний 6, оскільки є добутком трьох послідовних натуральних чисел.
Отриманий добуток обов’язково кратний 6, оскільки є добутком трьох послідовних натуральних чисел.
Отже, за принципом математичної індукції, вираз ![]() є цілим числом для всіх натуральних
є цілим числом для всіх натуральних ![]() .
.
Приклад 3. Довести , що сума кубів трьох послідовних натуральних чисел кратна 9.
Доведення
1) Сума ![]() ділиться на 9. Отже, твердження істинне, якщо першим із трьох послідовних чисел буде 1.
ділиться на 9. Отже, твердження істинне, якщо першим із трьох послідовних чисел буде 1.
2) Припустимо, що коли ![]() вираз
вираз![]() , де
, де ![]() - натуральне число ділиться на 9. Покажемо істинність твердження , коли
- натуральне число ділиться на 9. Покажемо істинність твердження , коли ![]() , тобто
, тобто ![]()
![]() Даний вираз кратний 9, оскільки перший вираз в дужках ділиться на 9 за припущенням, а другий – ділиться на 9 , бо це – добуток двох множників , один з яких дорівнює 9.
Даний вираз кратний 9, оскільки перший вираз в дужках ділиться на 9 за припущенням, а другий – ділиться на 9 , бо це – добуток двох множників , один з яких дорівнює 9.
За принципом математичної індукції , істинність твердження доведена для всіх натуральних ![]() .
.
Заняття 4
Доведення нерівностей методом математичної індукції
Приклад 1. ![]() Довести нерівність
Довести нерівність
Доведення. Вираз, що стоїть у лівій частині нерівності є сумою дробів, знаменники яких послідовно зростають від 1 до ![]() .
.
1) Якщо ![]() , то дана нерівність матиме вигляд
, то дана нерівність матиме вигляд ![]() і є правильною.
і є правильною.
![]() 2) Припустимо, що
2) Припустимо, що ![]() , і доведемо тоді , що правильною є і така нерівність
, і доведемо тоді , що правильною є і така нерівність
Розглянемо суму
![]() , де вираз позначений А є сумою
, де вираз позначений А є сумою ![]() дробів , кожен з яких більший від
дробів , кожен з яких більший від ![]() . Отже,
. Отже, ![]() і тоді
і тоді ![]()
Отже, за принципом математичної індукції , істинність нерівності доведена для всіх натуральних значень ![]() .
.
Узагальнення методу математичної індукції
Часто трапляється , що твердження , яке треба довести має місце не для всіх натуральних ![]() , а лише для значень
, а лише для значень ![]() , починаючи з певного натурального
, починаючи з певного натурального ![]() . У таких випадках користуються узагальненим принципом математичної індукції. Сформулюємо цей принцип.
. У таких випадках користуються узагальненим принципом математичної індукції. Сформулюємо цей принцип.
Нехай твердження , що залежить від натурального ![]() , задовольняє такі умови : 1) це твердження істинне при
, задовольняє такі умови : 1) це твердження істинне при ![]() ;
;
2)з правильності даного твердження при ![]() (для
(для ![]() ) випливає його правильність при
) випливає його правильність при ![]() . Тоді дане твердження справджується при всіх натуральних
. Тоді дане твердження справджується при всіх натуральних ![]() .
.
Приклад 2. Розв’язати нерівність ![]() .
.
Розв’язання
Безпосередня перевірка показує, що числа ![]() та
та ![]() не є розв’язками нерівності , а значення
не є розв’язками нерівності , а значення ![]() ,
, ![]() ,
, ![]() є її розв’язками. Природно виникає припущення, що розв’язками даної нерівності є натуральні числа
є її розв’язками. Природно виникає припущення, що розв’язками даної нерівності є натуральні числа ![]() . Доведемо це твердження методом математичної індукції.
. Доведемо це твердження методом математичної індукції.
1) Якщо ![]() , то нерівність правильна
, то нерівність правильна ![]()
2) Припустимо, що коли ![]() , нерівність правильна, тобто
, нерівність правильна, тобто ![]() , і доведемо, що тоді
, і доведемо, що тоді ![]()
Справді ![]() , оскільки
, оскільки ![]() для будь – яких натуральних
для будь – яких натуральних ![]() .
.
Тобто ![]() , якщо
, якщо ![]() ,
, ![]() . Тому розв’язками даної нерівності є всі натуральні числа
. Тому розв’язками даної нерівності є всі натуральні числа ![]() .
.
Приклад 3. Довести нерівність ![]()
Доведення
1) Якщо ![]() , то очевидна нерівність
, то очевидна нерівність ![]()
2) Якщо ![]() , то істинна нерівність
, то істинна нерівність
![]()
![]()
Доведемо істинність при ![]() , тобто
, тобто
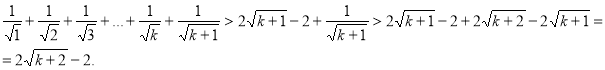
Нерівність ![]() можна довести методом від супротивного.
можна довести методом від супротивного.
Отже, вихідна нерівність справедлива при будь –якому натуральному ![]()
Заняття 5
Застосування методу в «нестандартних ситуаціях»
(економічних, геометричних, олімпіадних задачах)
Приклад 1. Доведіть, що довільну суму, більшу за 7 копійок, можна сплатити монетами вартістю в 3 копійки та 5 копійок.
Доведення
Індукцію проведем по числу копійок.
Суму у 8 копійок, очевидно, можна сплатити.
Припустимо, що нам вдалося сплатити суму в n копійок вказаними монетами. Якщо серед них є монета в 5 копійок, то замінимо її на дві монети по 3 копійки і одержимо суму в (n+1) копійку. Якщо ж всі монети суми по 3 копійки, то їх не менше трьох і, замінивши три монети по 3 копійки на дві монети по 5 копійок, ми також збільшимо суму на 1 копійку. Доведено.
Приклад 2. Довести, що загальна кількість діагоналей опуклого многокутника обчислюється за формулою ![]() , де
, де ![]() - кількість сторін .
- кількість сторін .
Доведення
1) Очевидно , що при ![]() ( для трикутника) формула справедлива, бо
( для трикутника) формула справедлива, бо ![]() .
.
2) Припустимо , що дана формула справедлива для ![]() , тобто загальна кількість діагоналей опуклого
, тобто загальна кількість діагоналей опуклого ![]() - кутника буде визначатись формулою
- кутника буде визначатись формулою ![]() Добудуємо до даного
Добудуємо до даного ![]() - кутника одну вершину і утворимо (
- кутника одну вершину і утворимо (![]() )- кутник. Нову вершину можна з’єднати з
)- кутник. Нову вершину можна з’єднати з ![]() вершинами вихідного многокутника, перебудованого нами в
вершинами вихідного многокутника, перебудованого нами в ![]() - кутник. Крім того одна з сторін многокутника перетворилась на діагональ. Тому загальна кількість діагоналей утвореного многокутника обчислюється за формулою
- кутник. Крім того одна з сторін многокутника перетворилась на діагональ. Тому загальна кількість діагоналей утвореного многокутника обчислюється за формулою ![]() .
.
Отже, загальна кількість діагоналей довільного опуклого многокутника обчислюється за формулою ![]()
Приклад 3. Довести, що число 11….1 (![]() одиниць) ділиться на
одиниць) ділиться на ![]() .
.
Доведення
1) Якщо ![]() , то число 111 ділиться на 3 (за ознакою подільності на 3).
, то число 111 ділиться на 3 (за ознакою подільності на 3).
Якщо ![]() , то число 111 111 111 ділиться на 9 (за ознакою подільності на 9).
, то число 111 111 111 ділиться на 9 (за ознакою подільності на 9).
Або 111 111 111 = 111*1001001. Кожен з множників ділиться на 3, а тому добуток ділиться на 9.
Якщо ![]() , то число 111…1 (27 одиниць) ділиться на 27, бо його можна представити
, то число 111…1 (27 одиниць) ділиться на 27, бо його можна представити ![]() . Перший множник ділиться на 9, а другий - на 3, тому число ділиться на 27.
. Перший множник ділиться на 9, а другий - на 3, тому число ділиться на 27.
2) Припустимо, що коли ![]() , то число
, то число ![]() ділиться на
ділиться на ![]() і доведемо , що число
і доведемо , що число ![]() ділиться на
ділиться на ![]() .
.
Виконаємо перетворення : ![]() . Перший множник ділиться на
. Перший множник ділиться на ![]() за індуктивним припущенням, а другий – на 3(за ознакою подільності), тому добуток ділиться на
за індуктивним припущенням, а другий – на 3(за ознакою подільності), тому добуток ділиться на ![]() .
.
За принципом математичної індукції , істинність твердження доведена для всіх натуральних ![]() .
.
Пам’ятайте, щонеакуратність у застосуванні методу математичної індукції може стати джерелом хибного твердження. Про це свідчить такий жарт.
«Доведемо» методом математичної індукції твердження: «Всі на світі коти — чорні». Один чорний кіт існує — це очевидно. Припустимо, що будь-які k котів є чорними. Візьмемо деяких k+ 1 котів і заховаємо їх у мішок. Якщо з мішка витягнути одного кота, то в мішку залишиться k котів, які за припущенням є чорними. Витягнемо з мішка ще одного кота (зрозуміло, що він — чорний), а в мішок заховаємо першого кота. Тоді в мішку знову буде k котів, які за припущенням є чорними. Заховуємо другого витягнутого кота в мішок. У ньому вже всі k+ 1 котів будуть чорними. Отже, за принципом математичної індукції, усі на світі коти — чорні.
Неправомірність цих міркувань полягає в тому, що не було перевірено істинності відповідного твердження при n1, адже висловлення «Будь-який один кіт є чорним» — хибне.
Удачі при вивченні математики.


про публікацію авторської розробки
Додати розробку
