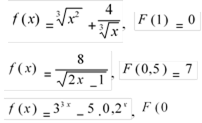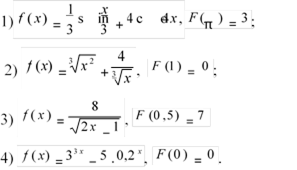Розробки уроків для самостійного вивчення теми "Інтеграл і його застосування"
Матеріали збірки переслідують головну мету: «Ввести систематизовані відомості про поняття первісної та інтегралу. Допомогти учням у вивченні матеріалу, результативному сприянню і усвідомленню нового матеріалу, набуттю навичок і умінь у розв'язуванні задач різного рівня складності, вчитися набувати знання самостійно, працювати в групах, парах, сприяти розвиненню логічного мислення, пам`яті і розширення кругозору» Розроблено картки – завдання для самостійної роботи, картки – тести, картки – завдання зі зразками розв'язання задач, практичні роботи, в яких використовуються знання всієї теми, завдання для тематичної атестації .На уроках при вивченні теми розглядаються зразки оформлення розв'язання задач з метою підготовки до зовнішнього незалежного оцінювання .
Харківська загальноосвітня школа І-ІІІ ступеня №130
Харківської міської ради Харківської області

Викладач математики Ляхова Тетяна Петрівна
Харків – 2018
|
ПОЯСНЮВАЛЬНА ЗАПИСКА Тематична папка використовується під час вивчення теми „ Інтеграл та його застосування» Ця папка містить десять уроків. Вона побудована відповідно до чинної навчальної програми з математики та містить орієнтоване планування теми та детальні роздаткові та дидактичні матеріали до уроків. Матеріали папки переслідують головну мету: «Ввести систематизовані відомості про поняття первісної та інтегралу. Допомогти учням у вивченні матеріалу, результативному сприянню і усвідомленню нового матеріалу, набуттю навичок і умінь у розв’язуванні задач різного рівня складності, вчитися набувати знання самостійно, працювати в групах, парах, сприяти розвиненню логічного мислення, пам`яті і розширення кругозору» Теоретичний матеріал подано компактно, запропоновані зразки розв’язання і оформлення задач, таблиці для наочного сприйняття матеріалу, довідковий матеріал. Розроблено картки – завдання для самостійної роботи, картки – тести, картки – завдання зі зразками розв’язання задач, практичні роботи, в яких використовуються знання всієї теми, завдання для тематичної атестації . На уроках теми розглядаються зразки оформлення розв’язання задач з метою підготовки до зовнішнього незалежного оцінювання . Майже на кожному уроці використовуються інноваційні технології навчання : „ Ажурна пилка ”, „ Інтерв’ю ” , „ Мікрофон ”, „ Незакінчене речення ”, „ Знайди помилку ”, „ Метеоритний дощ”, „ Наведи порядок”, „ Рюкзак”, „ Мозковий штурм” „ Знайди помилку ”, а також традиційні методи навчання. Учні повинні |
|
|
*знати : |
|
|
- означення , властивості первісної та інтегралу ; |
|
|
- правила знаходження первісної та інтегралу; - таблиця первісної ; |
|
|
- застосування інтегралу |
|
|
* уміти : |
|
|
-знаходити первісну для функції; |
|
|
- застосовувати обчислювальні формули ; - розв’язувати задачі на знаходження площі та об’єму тіл за допомогою інтегралу * цінувати : - розвиток мислення; - розвиток графічних умінь; - прагнення до ясності , простоти , раціональності ; - твердість у досягненні мети ; - здатність до результативної діяльності ; - ініціативність. |
|
|
|
|
|
Дидактичні та роздаткові матеріали , які подаються в папці , несуть у собі такі ознаки інноваційності :
1) можливість диференційованого та індивідуального підходу до вивчення матеріалу;
2) розвиток творчих можливостей учнів та самостійності у добуванні знань , підготовки їх до олімпіад та вступу до вищих навчальних закладів; Ефективність дидактичного та роздаткового матеріалу :
1) матеріали дають змогу економити час на уроці ;
2) матеріали дають змогу раціонально використовувати 12 – бальну систему оцінювання навчальних досягнень учнів;
3) матеріали забезпечують засвоєння та поглиблення знань і способів дій на рівні їх застосування і у новій ситуації.
|
|
|
ОРІЄНТОВНЕ ПЛАНУВАННЯ ТЕМИ «ІНТЕГРАЛ ТА ЙОГО ЗАСТОСУВАННЯ» (10 годин).
|
№ уроку |
Тема уроку |
Матеріал підручника |
|
1 |
Первісна. Основна властивість первісної |
§9, п1, контрольні запитання №1-9 задачі № 183,186 |
|
2 |
Правила знаходження первісної |
§9, п. 2 , контрольні запитання №1-4 Задачі №178,189 |
|
3 |
Задачі, що приводять до поняття інтегралу. Визначення інтеграла |
§9, п.1- 2 ,контрольні запитання №1-4 Задачі №188,190 |
|
4 |
Фізичний і геометричний зміст інтеграла |
§10, п.1-2 , контрольні запитання №1-7 задачі № 205,212 |
|
5 |
Визначений інтеграл, його властивості. Формула Ньютона - Лейбніця |
§10, п.1-2 , контрольні запитання №1-7 задачі № 207(10;11),215 |
|
6 |
Розв’язування вправ |
§10, п.1-2,контрольні запитання №1-4 задачі № 200;204 |
|
7 |
Застосування інтеграла |
§11, п.1-2,контрольні запитання №1-8 задачі № 207(4-5)210 |
|
8 |
Розв’язування вправ |
§11, п.1-2,контрольні запитання №1-8 задачі №207(7;9),213
|
|
9 |
Розв’язування вправ |
§10-11, скласти кроссворд за темою
|
|
10 |
Тематична атестація. |
Повторити матеріал , індивідуальні завдання |
УРОК № 1 ТЕМА «ПЕРВІСНА ТА ЇЇ ГОЛОВНА ВЛАСТИВІСТЬ »
I. Тест для діагностики готовності вивчення теми: «Інтеграл та його застосування»:
№
з\п ПИТАННЯ ВАРІАНТ ВІДПОВІДІ БАЛИ
А. x=3-2t Б. x= -2+3t 1
1. Яким є закон прямолінійного рівномірного руху точки, якщо її швидкість дорівнює 2, а координата в початковий момент часу t=0 дорівнює -3? В. x=2-3t Г. x=-3+2t
2. Матеріальна точка рухається вздовж координатної А. 0. Б. 3. 1 прямої за законом x= -2 sin t +t, де x- координата точки, t- час(t≥0). Якою є швидкість точки в В. -3. Г. -1. момент часу t=π?
3. При нагріванні тіла його температура змінюється А.2K\c. Б. 0,5 К\с. 1 за законом
Т= 0,5t +2, де Т- температура, К, t -час. З якою В. 0,5t К\с. В. Визначити швидкістю нагрівається тіло? неможливо
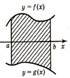
4. Яка з функцій f (x) = 2x чи g(x) = x 2 має більшу А. y= f(x) Б. y= g(x) 1 В. Мають одинакові
швидкість зміни в точці x = ? швидкості
Г. Визначити неможливо.
5. Скільки функцій мають ту саму похідну? А.Одна. Б. Дві. 1
В. Три. Г. Безліч
А. функція зростає на цьому 1 проміжку.
6. Якщо на деякому проміжку похідна тотожно Б. функція спадає на цьому дорівнює нулю, то…. проміжку.
В. функція є сталою на проміжку
Г. нічого певного сказати не можна.
7. Похідною якої фізичної величини є швидкість А. Закон руру. Б. Часу. 1 руху? В. Прискорення руху.
Г. Інша величина.
8. Похідною якої фізичної величини є прискорення А.Закон руру. Б.Часу. 1
руху? В. Швидкість руху. Г. Інша величина.
9. Серед наведених функцій укажіть функцію, А. y = C ⋅ f (x)⋅ 1 похідна якої дорівнює похідній функції y = f (x), y =− f (x) якщо С – довільне число. Б.
В. y = f (x) + C Г. y = fC(x)
10. Нерівномірно, залежно від змінної t , змінюється А. I = I0t Б.V = V0(1+ 0,1t) 1 величина… ρ=ρ0(t − t0) Г. Α= Nt2
В.
11.
 Тіло
рухається вздовж координатної прямої за А. t= 2. Б.
t =
12 . 1 законом x = 12 t2 −
4t +
5. В який
момент часу його В. t= 4. Г. t= 1. швидкість дорівнює нулю?
Тіло
рухається вздовж координатної прямої за А. t= 2. Б.
t =
12 . 1 законом x = 12 t2 −
4t +
5. В який
момент часу його В. t= 4. Г. t= 1. швидкість дорівнює нулю?
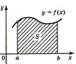
12. Чому дорівнює площа фігури, затушованої на рисунку?
А. 1. Б. 2. 1 В. 3. Г. Інша відповідь
II. Теоретичний матеріал до уроку
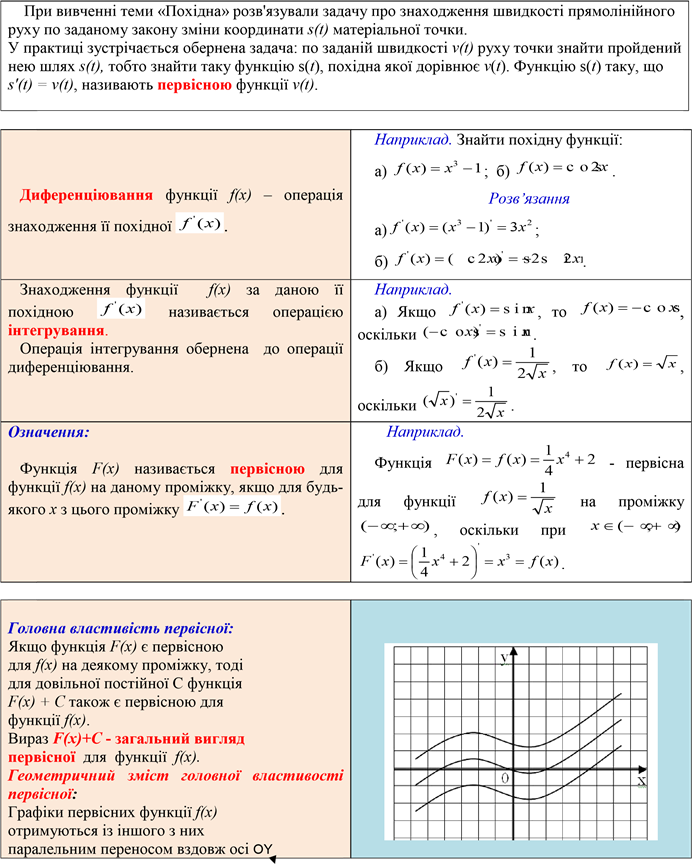
Занотуй в зошиті: Таблиця первісних
|
Функція f(x) |
Загальний вигляд первісних F(x) +C |
||||||
|
0 |
С |
||||||
|
1 |
х + С |
||||||
|
хn (n ≠ 1) |
|
xn+1
n +1 |
+C |
||||
|
|
1 х |
|
ln x + C |
||||
|
sin x |
-cos x + C |
||||||
|
cos x |
sin x + C |
||||||
|
|
1
cos2 x |
|
tg x + C |
||||
|
|
1 sin2 x |
|
-ctg x + C |
||||
|
ех |
ех + C |
||||||
|
ах |
|
ах
ln a |
+С |
||||
III. ЗРАЗКИ РОЗВ'ЯЗАННЯ ЗАДАЧ
Вчимося розв’язувати задачі
ЗАВДАННЯ 1 ( ІI рівень)
1. Довести ,що функція F(x) є первісною для функції f(x) на заданому проміжку:
a) F![]() для f
для f ![]() , де x
∈
(0; +∞)
, де x
∈
(0; +∞)
F′(x) =( ![]() ⇒
F(x) для f(x)
⇒
F(x) для f(x)
б) F(x) = 3x + cos ![]() для f(x) = 3
для f(x) = 3
![]() первісна
на R
первісна
на R
F′(x) = ( 3x + ![]() )′ = 3
)′ = 3 ![]() ) на R
⇒
F(x) первісна для f(x).
) на R
⇒
F(x) первісна для f(x).
ЗАВДАННЯ 2 ( ІІI рівень)
2. Для функції f(x) = x2 найти первісну, графік якої проходить через точку (3;7).
1 3 +
Розв’язання Первісна даної функції дорівнює f(x) : F(x)= 3 x
C. Графік F(x) проходить через точку (3; 7), її координати перетворюють рівняння F(x) =
![]() 13 3 + C в вірну
числову рівність: 9 + C = 7, C = – 2. Відповідь: F(x) = x
13 3 + C в вірну
числову рівність: 9 + C = 7, C = – 2. Відповідь: F(x) = x
РОЗВʹЯЗУВАННЯ ЗАДАЧІ ЗА ПЛАНОМ
(з обґрунтуванням кожного зробленого кроку )
ЗАВДАННЯ 3 ( ІІI рівень)
3. Графіки двох первісних для f(x) = x2 проходять через точки A(1; 5) и B(3; 8). Графік якої первісної розташований вище?
Розв’язання.
1) Для функції f(x) = x2 первісна дорівнює F(x)= 13 x 3 + C
2) виділимо
із множини всіх первісних F(x) ті, графіки яких проходять через
задані точки; 3) координати точки A(1; 5) дають 5= ![]() +C,
С = 4
+C,
С = 4 ![]() ;
;
![]() 1 3 + 4;
1 3 + 4;
4) через точку A(1; 5) проходить графік F(x)= 3 x
5) координати
точки B(3; 8) дають 8= ![]() ˑ 27 + С, С= -
1;
ˑ 27 + С, С= -
1;
1 3 - 1; 6) через точку B(3; 8) проходить графік первісної Ф(x) = 3 x
![]()
![]() 1 3 + 4 вище
1 3 + 4 вище
Відповідь. Графік першої первісної F(x)= 3 x
1 3 - 1 функції на 5 . графіка другої первісної Ф(x) = 3 x
Складемо послідовність виконання дій в подібних задачах.
Занотуй в зошиті:
Алгоритм виконання дій:
|
1 |
Знаходимо для даної функції f(x) первісну F(x). |
|
2 |
Записуємо множину первісних F(x) + C, C = const. |
|
3 |
Висновок: так як графік F(x) + C проходить через точку (a; b), тоді її координати задовольняють рівнянню F(a)+C= b и C =b – F(a). |
|
4 |
Записуємо рівняння первісної. |

 а) скільки
первісних має дана функція?
а) скільки
первісних має дана функція?
б) що можливо сказати про графіки цих функцій?
в) як отримати графік наступної первісної ?
3. Які властивості має похідна функції?
4. Які властивості має первісна функції?
5.Заповнити таблицю :
|
№ з\п |
Функція
|
Первісна |
|
1 |
f(x) = 5 |
F(x) = ... |
|
2 |
f(x) = 0 |
F(x) = ... |
|
3 |
f(x) = ... |
F(x) = – cos x + C |
|
4 |
f(x) = xm (m ≠ 1) |
F(x) = ... |
|
5 |
f (x)=25x |
F(x) = ... |
|
6 |
f(x) = cos kx |
F(x) = ... |
|
7 |
f(x) = ... |
F(x) = 12sin x + C |
|
8 |
2 4 f(x)= x +1 5x3 +1 7x |
F(x) = ... |
|
9 |
f(x) = ... |
|
|
10 |
45x2 f (x)= 2x −17 |
F(x) = ... |
Інтерактивна вправа: робота в малих групах.
![]()
Робота в малих групах дає змогу набути навичок спілкування та співпраці.
Після об’єднання у малі групи ви повинні за короткий час (8-10 хв.) виконати завдання та представити результати своєї роботи .
САМОСТІЙНА РОБОТА
|
|
І рівень - 3бала |
ІІ рівень - 3 бала
|
ІІІ рівень - 3 бала |
|
|
1.У «віконця » вписати
|
2.Чи є первісними для однієї і тієї ж функції наступні первісні: x +1 x
б) f(x) = x3, g(x) = x3 + 3x, h(x) = (x + 3)3, m(x) = x3 + 27? |
3. Найти для функції
|
|
|
|
2.Чи є первісними для однієї і тієї ж функції наступні первісні: а) f(x) = x2, g(x) = x2 + 3, h(x) = (x + 3)2; б) Ф(x) = cos 2x, Ф(x) = 2cos2 x? |
3. Графік однієї із первісних функції f(x) = x2 проходить через точку M(– 1; 10), а другої через точку N(2; – 6). Графік якої із них розташований вище? |
Самостійна робота
Учням пропонується розв’язати завдання різної складності – середньої, достатньої, високої. Завдання оцінюються у 7, 9, 11 балів. Учні самі обирають картки і розв’язують завдання напротязі 15 хвилин.
Зразки карток з диференційованими завданнями.
|
Середній рівень |
|||||||
|
Знайти первісну функції: |
|||||||
|
І варіант |
ІІ варіант |
||||||
|
1 |
у = 4х; |
2 |
у = 7х; |
1 |
у = 5х; |
2 |
у = 9х; |
|
3 |
у = 5; |
4 |
у = - 9; |
3 |
у = - 6; |
4 |
у = 19; |
|
5 |
3 у = х ; |
6 |
7 у = х ; |
5 |
2 у = х ; |
6 |
у = - х6; |
|
7 |
у = ( 2х + 3 ); |
8 |
у = ( - 5х + 1 ); |
7 |
у = ( 4 + 3х ); |
8 |
у = ( 5 - 8х ); |
|
9 |
у = ( 3х3 + х 2+5х) |
10 |
3 у =( 6х – 7х2 -4х) |
9 |
3 2 у=( х + 2х +7х) |
10 |
3 у=( х – 8х2 + 2х) |
|
11 |
у = - sin x; |
12 |
y = 1 / cos2 x. |
11 |
у = 1 / sin 2 x; |
12 |
y = cos x. |
Достатній рівень
Знайти первісну функції:
І варіант ІІ варіант
1 у = (2х + 3 ); 2 у = ( - 7х + 1); 1 у = (4х - 3 ); 2 у = ( - 7х + 1);
3 у = 6 / x ; 4 у = - 9/ 2 x ; 3 у = - 3 / 2 x ; 4 у = 2 / ;
5 у = 32 х31 ; 6 у = -118 х11[1]; 5 у = - 43 х44 ; 6 у = 612 х 611;
7 у = ( 2х4 + 3х ); 8 у = ( - 5х6 + 15х ); 7 у = ( 6х3 - 5х ); 8 у = ( - 5х4 + 8х ); 9 у = ( 3х + 7 )2; 10 у = ( 6х – 4 )9; 9 у = ( 3х + 5 )5; 10 у = ( 4х – 7 )7; 11 у = - sin 6x; 12 y = 5 / cos2 10x 11 у = sin 106x; 12 y = 3 / cos2 30x.
Високий рівень
Знайти первісну функції:
І варіант ІІ варіант
1 у=(2х2 + 3 ); 2 у=(- 6х +3 /4х2); 1 у = (4х3 + 7х ); 2 у =(- 9 √х – 5х );
3 у = 16 / 16x ; 4 у = - 5/ 2 15x ; 3 у=-3 / 2 12x ; 4 у = 7/ 14x ;
5 у=36(3х + 1 )35 ; 6 у=-115(4х – 5)116; 5 у=-43(2х + 5)44 ; 6 у=612(- 5х–8 )611;
 7
у = ( 2х4 + 3х ); 8 у = ( - 5х6 + 5х ); 7
у = ( 6х3 - 5х ); 8 у = ( - 5х4 + 3х ); 9 у =25( 2х + 7 )4; 10 у = 100( 6х – 4 )9; 9 у=36( 3х + 7 )5;
10 у=49( 4х - 4 )7;
11 у=-12sin (16x +5) 12
y = 5 / 3cos2 10x. 11 у = 45 sin 5x; 12 y=3 / 4 cos2 30x. V. Рефлексія
7
у = ( 2х4 + 3х ); 8 у = ( - 5х6 + 5х ); 7
у = ( 6х3 - 5х ); 8 у = ( - 5х4 + 3х ); 9 у =25( 2х + 7 )4; 10 у = 100( 6х – 4 )9; 9 у=36( 3х + 7 )5;
10 у=49( 4х - 4 )7;
11 у=-12sin (16x +5) 12
y = 5 / 3cos2 10x. 11 у = 45 sin 5x; 12 y=3 / 4 cos2 30x. V. Рефлексія
Учням пропоную висловитися з питання:
1.Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).2.Чи отримали ви задоволення від власної праці?
3.Чи вичерпали ви свої можливості?4.Що тобі сподобалось на уроці?
5.Порівняйте свої знання на початку уроку і в кінці
VI.Домашнє завдання
§9, п1, контрольні запитання №1-9
задачі № 184,186
Практичне завдання :
1. Запишіть первісні для функцій:
УРОК № 2 ТЕМА «ПРАВИЛА ЗНАХОДЖЕННЯ ПЕРВІСНОЇ
I. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ Метод «НАВЕДИ ПОРЯДОК»
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.

(Одна правильна відповідь оцінюється в 1 бал) 1. Що називається інтегруванням функції? 2. Визначення первісної.
3. Умова існування первісної.
4. Признак сталості функції.
5. Геометричний зміст первісної. 6. Заповнити таблицю:
|
f(x) |
x , n≠1 |
sin x |
|
k |
1 |
cos x |
x12 |
1 sin2 x
|
|
F(x) |
|
|
|
|
|
|
|
|
n
Самостійна робота
Робота в парах , перевір свого сусіда по парті і постав оцінку:
( за кожну правильну відповідь – 1бал)
1. Гра «Встановіть відповідність»
|
Функція |
Відповідність |
Первісна |
|
0 |
|
|
|
1 |
-cos x + C |
|
|
n х (n≠ 1) |
С |
|
|
|
sin x + C |
|
|
sin x |
х + С |
|
|
cos x |
lnx + C |
|
|
1 − 2 x sin |
-ctg x + C |
|
|
1
х |
tg x + C |
|
|
ех |
ax C lna + |
|
|
1
|
5 |
|
|
|
15sin x 3 |
|
|
(2x+3)4 |
|
|
|
5cos x 3 |
|
|
|
|
(2x + 3)5 C + 1 0 |
|
|
х |
х |
а е + C
II. ТЕОРЕТИЧНИЙ МАТЕРІАЛ З ТЕМИ
Правила знаходження первісних
|
Правило 1. Якщо F - первісна функції f (x) , а G – первісна
|
Наприклад. Знайти первісну для функції:
Розв’язання |
|||
|
а) б) |
2 |
|
||
|
F(x) =−c ox +ss ix +nC |
. |
|||
|
|
Наприклад. Знайти первісну для функції:
Розв’язання а) F(x) = 4t g x+C ; F(x) = 1 ⋅ ax + C = ax + C. б) 5 l an 5l an
|
|||
|
1 F(k x+ b) - первісна для
|
Наприклад. Знайти первісну для функції:
|
|||
ЗАНОТУЙ В ЗОШИТІ:
|
Правило |
I |
II |
III |
||
|
Функції |
f + g |
kf |
f(kx +b) |
||
|
Первісні |
F + G |
kF |
|
1 k |
F(kx+b) |
III. РОЗВʹЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ :
Вчимося розв’язувати задачі.
|
1. Знайти загальний вигляд первісної для функції: |
а) f (x) = x14 − c ox ;
|
|||||||||||||
|
Розв’язання: |
||||||||||||||
|
а) 1) Використаємо
|
|
. функції є |
f (x) = x−4 −c ox ;
( − 4 +1 −
Відповідь: F(x) =−−s i nx +C . |
|||||||||||
|
для первісною
|
||||||||||||||
|
б) 1) Використаємо, якщо |
|
|
f F
|
C ; |
||||||||||
|
- первісна для функції
2) Використаємо: f - первісною є F(x) = 2 x . |
|
, то функції: функції |
||||||||||||
|
для для функція |
||||||||||||||
|
|
2 2 2 2 F Відповідь: F |
|
||||||||||||
|
2. Для функції первісну, графік якої проходить через точку А: |
|
знайти |
а) f (x) = 5s i n2x +
2c o3x ,
Аπ |
|
||||||||||
|
|
||||||||||||||
|
Розв’язання:
|
|
|||||||||||||
|
1) Для функції первісну в загальному вигляді. 2) підставимо знайдемо значення С. |
|
запишемо
точки А і |
F(x) = 5⋅ 1 x а) 1 ⋅− c 2o + 2s⋅ 13 ⋅s 3ix +nC;
F 2 − =
−1 c 0π 3 2 3 2
Відповідь: F . |
|
||||||||||
|
У записану рівність замість х абсцису
|
||||||||||||||
IV. Закріплення вивченого матеріалу

ПЕРЕВІР СЕБЕ! ІНДИВІДУАЛЬНА РОБОТА
«ТЕСТ»
|
Рівень |
Завдання
|
Варіант відповіді |
Бали |
|
1 |
1. Множина первісних для функції: f (x) = 2+s i nx має вигляд: |
а) F(x) = 2x−c ox+sC F(x) = 2x+c ox+sC в) F(x) = 2+c ox+sC ; |
1 |
|
2.Знайти загальний вигляд первісних для функції: y=5x4 . |
а) 20x3 +C ; б) x55 +C ; в) x5 +C ; |
1 |
|
|
3.Знайти загальний вигляд первісних для функції: y=x2 +1. |
x33 C ;б) x3 + x+C в) x33 + x +C ; а) + |
1 |
|
|
2 |
4. Графік якої з первісних функції: f (x) = x 4 проходить через точку А1;2 15 ? |
а) F(x) = 5x4 − 2 54 б) F(x) = x55 + 2; в) F(x)
=
4x3 −1 |
1,5 |
|
|
а) F(x) =−3t g(3x−2)+C ; б) F(x) = в) F(x)
=
|
1,5 |
|
|
3 |
6. Швидкість тіла, що рухається прямолінійно, виражається формулою V(t) = 4t3 − 3t2 + 2 . В початковий момент тіло перебувало у початку координат. Якою формулою виражається залежність координати х від часу t? |
а) x(t) =1 2t 2 + 6t ; б) x(t) = t 4 −t 3 + 2t ; в) x(t) =1 t64 −9t 2 + 2t ;
|
1 |
|
1 f(x) = c o s2x − s i n2 x ;
|
а) F(x) = б) F(x) =t g2x + c t g+ C
|
1 |
|
|
8. Знайти первісну функції
|
а) F(x) = 4(3− 2x) б) F(x) =
|
1 |
ІІІ. Узагальнення знань, вмінь і навиків
![]() Інтерактивна вправа: робота в малих групах.
Інтерактивна вправа: робота в малих групах.
Учні об’єднуються у три різнорівневі групи. Кожна група отримує завдання відповідного рівня складності. Учні записують розв’язки у зошит, а один представник від групи працює біля дошки.
Знайти первісну функції:
Середній рівень Достатній рівень Високий рівень
 •
у = - 6 sin x + 3;
• у = cos 5х + 5х; •
у =15 sin(3х+5) +10
cos(4х– 6) • y = 6х5 – 7х6; • у = 5х2 – 7; • у = 30 ( 1 / 5* х)6 – (1 -2х)2 • у = 2х + 1 • у = 5 ( 1/
2 x ) – • у = 6 / (3х2) – 9 .
•
у = - 6 sin x + 3;
• у = cos 5х + 5х; •
у =15 sin(3х+5) +10
cos(4х– 6) • y = 6х5 – 7х6; • у = 5х2 – 7; • у = 30 ( 1 / 5* х)6 – (1 -2х)2 • у = 2х + 1 • у = 5 ( 1/
2 x ) – • у = 6 / (3х2) – 9 .
2х
Якщо є час, то далі можна запропонувати учням першої групи придумати 1 – 2 завдання на обчислення первісної для учнів 2 групи, учням другої групи – аналогічне завдання для учнів 3 групи. У цей час відбувається опитування учнів 3 групи. Потім учні 2 та 3 груп розв’язують отримані завдання, а учні 1 групи розв’язують додаткові вправи.
Математичний диктант
Щоб перевірити правильність написання диктанту, викладач зачитує правильні відповіді, а учні ставлять “ + ”, якщо відповідь правильна, і “ - ”, якщо відповідь неправильна або відсутня. Оцінка відповідає кількості правильних відповідей, тобто кількості знаків “ + ”.
|
№ з/п |
ЗАВДАННЯ |
|
1 |
Напишіть правила обчислення первісної у вигляді формул. |
|
2 |
Проілюструйте на малюнку головну властивість первісної. |
|
3 |
Напишіть таблицю первісних елементарних функції. |
|
4 |
Знайдіть первісні для функцій: 1 11
1 1
|
САМОСТІЙНА РОБОТА НАВЧАЛЬНОГО ХАРАКТЕРУ
Використовуючи твердження, перевір себе
Варіант 1
|
Рівень |
Завдання |
Бали |
|
1 |
1. Доведіть, що функція F(x) є первісною для функції f(x) на вказаному проміжку:
в) F(x) = 3x + cos , f(x) = 3 , х є (- ∞ ; + ∞ ); |
3 |
|
2 |
2. Знайдіть всі первісні для функції: 1 a) f(x) = 5; б) f(x) = х5; в) f(x) = х ; |
3 |
|
3 |
3. Для даної функції f(x) знайдіть первісну, графік якої проходить через задану точку А: 1
|
3 |
Варіант 2
|
Рівень |
Завдання |
Бал и |
|
1 |
1.Доведіть, що функція F(x) є первісною для функції f(x) на вказаному проміжку:
а) F(x) = (2х + 1)3; f(x) = 6(2х + 1)2, х є (- ∞ ; + ∞ );
б) F(x) = sin2х, f(x) = sin 2х, х є (0; + ∞ ).
2
|
3 |
|
2 |
2. Знайдіть всі первісні для функції: 1
|
3 |
|
3 |
3. Для даної функції f(x) знайдіть первісну, графік якої проходить через задану точку А: 1
|
3 |
 Інтерактивна вправа «Метод незакінченого речення»
Інтерактивна вправа «Метод незакінченого речення»
![]() 1. Функція F(x)
називається первісною для функції f(x) на заданому проміжку, якщо … 2.
Будь-яка первісна для функції f на проміжку I може бути записана в вигляді
… n, 4) f(x) = x12
, 5) f(x) = cos12 x ,
1. Функція F(x)
називається первісною для функції f(x) на заданому проміжку, якщо … 2.
Будь-яка первісна для функції f на проміжку I може бути записана в вигляді
… n, 4) f(x) = x12
, 5) f(x) = cos12 x ,
3.Якщо 1) f(x) = cos x, 2) f(x) = k, 3) f(x) = x
1 1
6) f(x)= sin x
, 7) f(x) = ![]() , 8) f(x) = sin2 x , тоді
загальний вигляд первісної буде записаний у вигляді…
, 8) f(x) = sin2 x , тоді
загальний вигляд первісної буде записаний у вигляді…
4. Знаходження функції за даною похідною називається …
5. Первісна суми функцій дорівнює …
6. Первісна добутку числа і функції дорівнює добутку …
7. Якщо функція F(x)- первісна для функції f(x), то функція 1k F(k x+ b) - первісна для функції … , де …
8.З´ясувати, для якої із функцій: f1 = sin3x, f2 = -3sin3x, f3 = -sin3x – sin π, f4 = 3sin3x функція F(x) = cos 3x – cos π є первісною на ( - ∞; +∞)?
9. Знайти загальний вигляд первісних для функцій: а) f(x) = 8, б) f(x) = 2x
VI. Рефлексія
Учням пропоную висловитися з питання:
1. Порівняйте свої знання на початку уроку і в кінці.
2. Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).
3. Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).
3. Чи отримали ви задоволення від власної праці?
4. Чи вичерпали ви свої можливості?
5. Що ти хотів би змінити під час уроку?
VII. Домашнє завдання
§9, п. 2 , контрольні запитання №1-4 Задачі №178,189
Завдання на картках:
|
№з\п |
Завдання |
||||
|
1 |
Довести, що функція F є первісна для функції f на R а) F(x) = x2 – sin2x – 1, б) F(x) = 3x5 – cos2 x + 2, f(x) = 2x – 2cos2x. f(x) = 15x4 + sin2x. |
||||
|
2 |
Найти загальний вигляд первісної для функції: |
||||
|
а) f(x) = (3x +2)4 - |
1 x6 |
+ 7; б) f(x) = 5x4 + sin x. в) f(x) = 5 - |
2 1 3
+ x |
. |
|
|
3 |
Для функції f найти первісної F, яка приймає дане значення в відповідній точці: 3 5
|
||||
УРОК № 3 ТЕМА « ПРИКЛАДИ ЗАДАЧ, ЩО ПРИВОДЯТЬ ДО
ПОНЯТТЯ ІНТЕГРАЛА. ОЗНАЧЕННЯ ІНТЕГРАЛА »
 I. ПЕРЕВІРКА ДОМАШНЬОГО
ЗАВДАННЯ Інтерактивна вправа « МІКРОФОН»:
I. ПЕРЕВІРКА ДОМАШНЬОГО
ЗАВДАННЯ Інтерактивна вправа « МІКРОФОН»:
Питання інтерактивної технології „ Мікрофон ”
1. Що називаємо первісною для функції f(x)?
2. Чи правда що F(x) = x2 є первісною для функції f(x) = 2x.
3. Яка теорема показує, як пов’язані між собою всі первісні даної функції?
1
4. Чи вірно, що первісна функції f(kx+b) дорівнює k F(kx+b)?
5. Що ми називаємо невизначеним інтегралом?
6. Яка первісна функції ех (F(x) = )?
7. Чи є функція F(x) = 3x2+x-2 первісною для f(x)=6х+1?
8. Чи є функція F(x) = 5 – 3x первісною для функції f(x) = –3 ?
9. Що являє собою загальний вигляд первісної для f(x) = ?
Метод «Метеоритний дощ»
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.
 F(x)=⊗
x+⊗
F(x)=⊗
x+⊗
II.ТЕОРЕТИЧНИЙ МАТЕРІАЛ З ТЕМИ
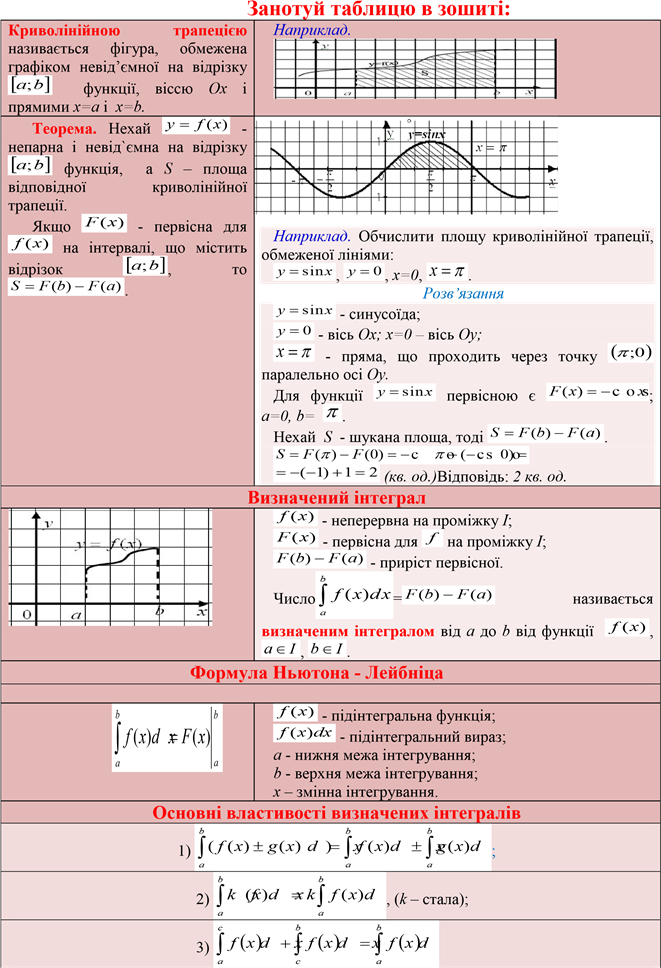
III. РОЗВ`ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ :
Вчимося розв’язувати задачі.
|
1. Обчислити інтеграл: |
|
π
6 |
. |
||||||||||||
|
Розв’язання: |
|||||||||||||||
|
1) Знайдемо первісну підінтегральної функції. 2) У первісну замість х підставимо спочатку верхню межу інтегрування, потім – нижню та обчислимо різницю одержаних значень. |
|
||||||||||||||
|
Відповідь: а) |
2 |
; б) 8; в) 1; г) |
4 |
. |
|||||||||||
|
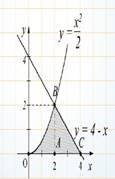
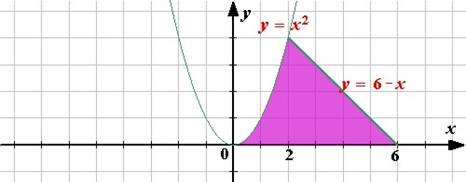
2.Обчислити площу фігури, обмеженої лініями: |
а) |
y=x2 +2 |
; |
y = 4−x |
; |
||||||||||
|
|
|
||||||||||||||
|
Розв’язання: |
|||||||||||||||
|
а) 1) В одній системі координат будуємо дані лінії. |
(
|
|
- парабола, вітки якої напрямлені вгору
вершина параболи.
пряма, яка проходить через т |
||||||||||||
а=1, а > 0). (0;2) – |
|||||||||||||||
|
2) Знаходимо абсциси точок перетину даних ліній – межі інтегрування. 3) Обчислимо площу утвореної фігури, використавши: b
a
|
x1 = −2 ; x2 =1. а=-2, b=1 – 1 = ∫(4− x − x2 −2)d −2
|
|
; + 2)d =
|
||||||||||||
|
межі інтегрування.
|
|||||||||||||||
|
|
2 |
(кв.од). |
|||||||||||||
IV.  АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
ПЕРЕВІР СЕБЕ! ІНДИВІДУАЛЬНА РОБОТА
«ТЕСТ»
|
Рівень |
Завдання |
Варіант відповіді |
Бали |
|
|
|
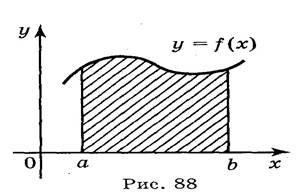
1.Серед фігур, зображених на рисунках, криволінійною трапецією є:
|
Б В |
1 |
|
|
2. Первісною для функції f (x) = 3x 2 + 4x −1 є: |
А. F(x) = x+ 4 Б. F(x) = x3 + 2x 2 − x В. F(x) = 3x3 + 4x 2 − x |
1 |
||
|
3. Серед даних рівностей формулою Ньютона – Лейбніца є:
|
b А ∫ f (x)d =xF(b) + F(a) a b Б ∫ f (x)d =xF(b)⋅F(a) a b В ∫ f (x)d =xF(b) − F(a) a |
1 |
||
|
|
4. Для функції f (x) = − x13 +s i nx первісною, записаною в загальному вигляді є: |
А. F(x) = − x34 + c ox +sC Б. F(x) = x14 +c ox+sC В. F(x) = x12 − c ox +sC |
1 |
|
|
5. |
А. 4 12 Б. 8 В. 4 |
1 |
||
|
6. Фігура, обмежена лініями y =
0,
y =cosx , x =
− зображена на рисунку: |
А Б В
|
1 |
||
|
|
7. Для функції f (x) = 2x(x 2 +1) первісною, графік якої проходить через точку М(1;2), є: |
А F(x) = 12 x4 + x2 + 12 Б F(x) = 1 x4 + x2 − 1 2 2 В F(x) = 2x 4 + x 2 −2 |
1 |
|
|
2 |
d x
|
А. 2c o s (5−2x)+C 1 − c o5s (− 2x) + C 2 В. |
Б. |
1 |
|
9.Для функції f (x) = 3c o s3x первісною,графік якої проходить через точку B18
|
А. F(x) = 3s i n3x + 12 Б. F(x) = −3s i n3x − 12 В. F |
|
1 |
|
|
4 |
|
А. 91 Б. 87 В. 64 |
|
1 |
|
11. Щоб обчислити площу фігури, обмеженої лініями y=2x2 і y=x2 +x+2, треба обчислити:
|
1 А. ∫( (x2 + x+2)−2x2)d −2
В. ∫(2x2 −(x2 + x + 2))d −2 |
|
1 |
|
|
|
2 1 А. 3 кв.од. Б. 2 кв.од. В.1кв.од. |
|
1 |
|
САМОСТІЙНА РОБОТА
 Учні самостійно
вибирають завдання за рівнями:
Учні самостійно
вибирають завдання за рівнями:
|
Рівень |
№ картки |
Бали |
|
Середній рівень |
картки № 1-2 |
4-6 |
|
Достатній рівень |
картки № 3-4 |
7-9 |
|
Високий рівень |
картки № 5-6 |
10-11 |
|
Картка №1 |
Картка №2 |
||
|
Найти визначений інтеграл |
|||
|
1) −2 |
3 x d x 5 x d 2) ∫1 7 + ∫3 7 |
1) ∫ −3 |
2) |
|
3) d |
3) |
|
|
|
4)
|
5) d x |
4) |
π
|
|
Картка №3 |
Картка №4 |
||
|
Найти визначений інтеграл |
|||
|
4 1) ∫(x5 − 6x)d x −4 |
5 1) ∫(− 2x7 + 8x)d x −5 |
||
|
2) |
|
||
|
2 3x2d x 4 3x2d x 3) ∫1 7 + ∫2 7 |
3 5x3d x 3 5x3d x 3) ∫1 8 − ∫5 8 |
||
|
2π π
3
|
π π
|
||
|
|
|
||
|
Картка №5 |
Картка №6 |
||
|
Найти визначений інтеграл |
|||
|
6 1) ∫(x7 + 9x3)d x −6 |
7 1) ∫(3x4 − x5)d x −7 |
||
|
|
2) |
||
|
|
|
||
|
|
|
||
![]() Інтерактивна вправа: робота в малих
групах.
Інтерактивна вправа: робота в малих
групах.
Робота в малих групах дає змогу набути навичок спілкування та співпраці.
Після об’єднання у малі групи ви повинні за короткий час (8-10 хв.) виконати завдання та представити результати своєї роботи . Робота 2-3 рівнів:за виконання одного завдання –
3 бала
ЗАВДАННЯ.
|
Малюнок |
І група |
ІІ група |
ІІІ група |
|
|
Знайти :
Площу криволінійної трапеції ОВА.
|
Знайти :
Площу криволінійної трапеції АВС.
|
Знайти :
Площу криволінійної трапеції ОВС.
|
|
|
Дано криволінійну трапецію. Знайдіть : |
||
|
1. Границі інтегрування. 2. Загальну формулу обчислення даної площі за допомогою інтеграла. 3. Площу цієї криволінійної трапеції.
|
|||

V.Повторення вивченого матеріалу
Інтерактивна вправа: «Метод незакінченого речення…»
1. Функція F( x ) називається первісною для функції f( x ), якщо …
2. Неозначеним інтегралом називають…
3. Первісна функції f(k x +b) дорівнює…
4. Формула для обчислення площі фігури…
5. Криволінійною трапецією називається фігура…
6. Означеним інтегралом є …
7. Площа криволінійної трапеції це…
8. Знаходження функції за даною похідною називається …
9. Інтеграл від суми функцій дорівнює …
10.Інтеграл добутку числа і функції дорівнює добутку…
Коментоване розв`язування завдань
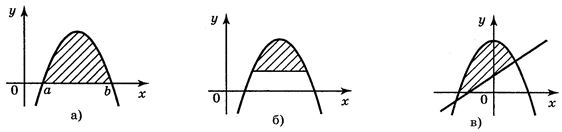
1. Які із заштрихованих на рисунку фігур є криволінійними трапеціями, а які — ні?
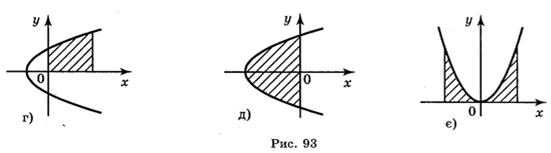
2.Побудуйте криволінійні трапеції:
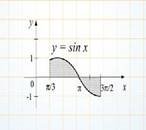
а) у = x2, x = 1, x = 2, у = 0; б) у = sin х, x = 0, x = π, y = 0;
![]() в) у = е·*", x =
0, x = 1, y = 0; r) y = x , x = 0, x = 4, у = 0.
в) у = е·*", x =
0, x = 1, y = 0; r) y = x , x = 0, x = 4, у = 0.
3. Обчисліть приблизно площу криволінійної трапеції, обмеженої лініями у = 2x , х = 0, х =4, у = 0, розділивши відрізок [0; 4] на чотири рівні частини і побудувавши східчасту фігуру із прямокутників.
(Відповідь: 7,5)
VII. Домашнє завдання
§9, п.1- 2 , контрольні запитання №1-4
Задачі №190,188
Домашнє завдання: ( 4-е завдання для більш підготовлених учнів).
1. Довести, що функція F(х) = 3х4 є первісною для функції f(х) = 12х3 на проміжку (- ∞ ; + ∞ );
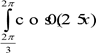 d x
d x
2.Вичислити інтеграл
![]() π
π
3.Знайти площу криволінійної трапеції,
обмеженої лініями у = cos x, у =0, х = - ![]() 2 , x = .
2 , x = .
4.Вичислити площу фігури, обмеженої лініями у = х + 3, у = 0, х = 1 и х = 3.
УРОК № 4 ТЕМА «ФІЗИЧНИЙ ТА ГЕОМЕТРИЧНИЙ ЗМІСТ
ІНТЕГРАЛА»
I. Перевірка домашнього завдання
По готовому домашньому завданню, раніше зробленому викладачем на дошці учні виконують самоперевірку, виставляють оцінку в зошит та лист самооцінки:
Завдання 1
Довести, що функція F(х) = 3х4 є первісною для функції f(х) = 12х3 на проміжку (- ∞ ; + ∞ );
Рішення. За визначенням первісної F´ (х) = f (х). Отже, F’ (х) = (3х4)’ = 3•4•х3 = 12х3 = f (х) для всіх х €(- ∞ ; + ∞ );
Завдання 2
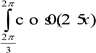 d x Обчислити
інтеграл
d x Обчислити
інтеграл
Рішення.
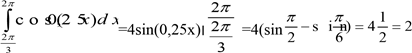
Завдання 3
Знайти площу криволінійної трапеції, обмеженої лініями у = х + 3, у = 0, х = 1 и х = 3.
Рішення. Намалюємо лінії, задані рівняннями та побудуємо криволінійну трапецію, площу якої будемо знаходити.
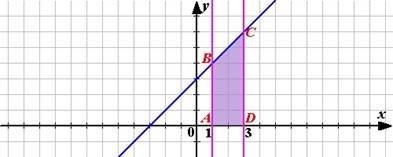
SАВСД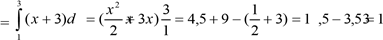
Відповідь: 10 кв.од.

II. Повторення теоретичного матеріалу
1. Інтерактивна технологія „Робота в парах”
Учні об’єднуються парами , відповідають на питання , поставлені один одному , таким чином повторюють теоретичний матеріал та готуються до виконання навчальної самостійної роботи : один учень відповідає на питання парних номерів списку , а інший – непарних .
Питання.
• 1.Сформулювати признак сталості функції.
• 2.Сформулювати основної властивості первісної.
• 3.В чому полягає геометричний зміст основної властивості первісної?
• 4.Скільки правил знаходження первісної ти знаєш? Назви їх.
• 5.Дати визначення криволінійної трапеції.
• 6.Сформулювати теорему про площу криволінійної трапеції.
• 7.Що називається інтегралом?
• 8.Запишіть на доці формулу Ньютона - Лейбніца і дайте роз’яснення цій формулі.
ІНТЕРАКТИВНА ВПРАВА «МОЗКОВИЙ ШТУРМ»
Теоретичний багаж ваших знань по темі «Інтеграл» достатній. Перевіримо, як ви вмієте застосовувати його на практиці.
1. Чи вірні наступні рівності:
а).![]() в).
в).![]() ; г)
; г) ![]() ;
д)
;
д) ![]() x ;
x ;
![]()
![]() є) ∫3 5d = x52x23 = 52 (32 −02) = 4 ; ж) ∫1 x2d =xx331 = 13(1−0) = 13
;
є) ∫3 5d = x52x23 = 52 (32 −02) = 4 ; ж) ∫1 x2d =xx331 = 13(1−0) = 13
;
2
00 00
2.Чи є фігура, яка зображена на малюнку криволінійною трапецією? (опрацювання
задач 1,2,3,4,5)
Задача 1. Задача 2.
![]() .
.
Задача 3. Задача 4.

3.Записати за допомогою інтеграла формулу, за якою знаходиться кожна
площа, зображена на малюнках вище
III. ТЕОРЕТИЧНИЙ МАТЕРІАЛ
|
Знаємо, що коли x=x(t) –закон руху матеріальної точки, тобто залежність її координати від часу, то x´(t)=v(t).Це означає, що функція x=x(t)- одна із первісних для функції v= v(t). Отже, переміщення точки дорівнює приросту первісної для функції v= v(t) на проміжку ( tº;T).
|
Зверніть увагу, що значення інтегралу не залежить від вибору первісної для підінтегральної функції. |
|
Фізичний зміст інтеграла. Інтеграл ʃ V(t)dt при V(t) ≥ 0 дорівнює шляху, пройденому матеріальною точкою, яка рухається прямолінійно зі швидкістю V= v(t), за проміжок часу ( tº;T). |
|
|
Геометричний зміст інтеграла. Інтеграл ʃ f(x)dx від невід´ємної неперервної на відрізку (а;в) функції y=f(x) дорівнює площі криволінійної трапеції, обмеженої графіком цієї функції і прямими y=0, x=a, x=b. |
|
IV. РОЗВЯЗУВАННЯ ЗАДАЧ
ОБГРУНТОВУЮЧИ КОЖНЕ ТВЕРДЖЕННЯ, ПЕРЕВІР СЕБЕ
ЗАВДАННЯ ІV рівень
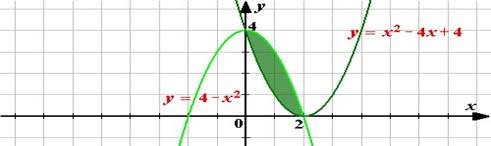
Фігура, обмежена лініями у = -2х + 8, х = -1, у = 0, поділяється лініями у = х2 – 4х + 5 на дві частини. Обчислити площу кожної частини.
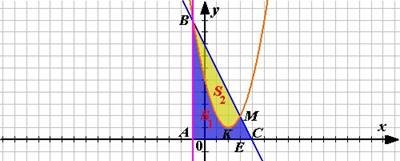
Рішення.
1.Розглянемо функцію у = х2 – 4х +5. Після перетворень отримаємо: у = х2 – 4х +5 = (х2 – 4х + 4) – 4 + 5 = (х – 2)2 + 1, тобто графіком даної функції є парабола с вершиною К(2; 1).
2. S = 2 •
∆АВС 1 5•1 0= 2 5.
3. SАВКМЕ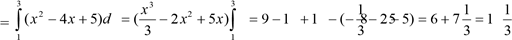
4. S1 = SАВКМЕ + S∆ЕМС, S1 = 13![]()
5. S2 = S∆АВС
– S![]() .
.
Відповідь: S1=14
![]() (кв.од)
(кв.од)![]() (кв.од.)
(кв.од.)
Завдання III рівень
Знайдіть площу фігури, обмеженої параболами у = х2 і у = 2х - х2 та віссю ОХ.
Рішення
![]()
![]() Побудуємо графіки
функцій у = х2 і у = 2х - х2 і
знайдемо абсциси точок перетину цих графіків із рівняння: х2 = 2х – х2.
Корені цього рівняння х1 = 0, х2 =
1.
Побудуємо графіки
функцій у = х2 і у = 2х - х2 і
знайдемо абсциси точок перетину цих графіків із рівняння: х2 = 2х – х2.
Корені цього рівняння х1 = 0, х2 =
1.
Ця фігура складається з двох криволінійних трапецій: ОАВ і ВАС.
Отже, шукана площа дорівнює сумі площ цих
![]() трапецій: S =∫1 x2d +∫2 (2xx− x2)d
=
x3x1+x2 − x3 2 =1
трапецій: S =∫1 x2d +∫2 (2xx− x2)d
=
x3x1+x2 − x3 2 =1
0 1 30 3 1
Відповідь: S=1 ( кв.од.)
 V Актуалізація опорних
знань, умінь і навиків УСНА
ВПРАВА
V Актуалізація опорних
знань, умінь і навиків УСНА
ВПРАВА
1. ![]()
![]()
![]()
![]() Які з функцій y = 2 x, y = 4 x
, y = 2 x +3 , y = x -1 є
первісними функції y
Які з функцій y = 2 x, y = 4 x
, y = 2 x +3 , y = x -1 є
первісними функції y
1
= ![]() ?
?
2. Знайти загальний вид первісної для функцій : а) у =7,5; б) y= 12 x + x4; в) y=2 sinx ⋅ cosx
3. Скажіть, як знайти за допомогою інтеграла знайти площу фігури Ф?
`
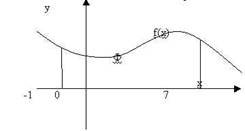
4. Представити площу заштрихованої фігури як суму чи різницю площ криволінійних трапецій, обмежених графіками відомих вам ліній.
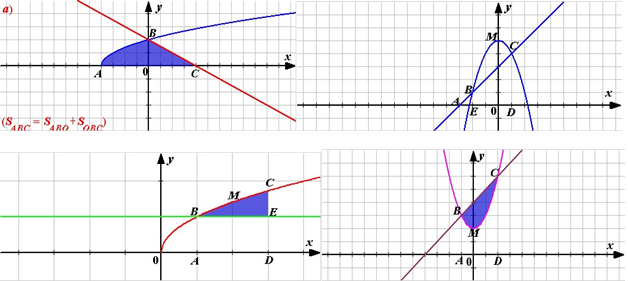
VI Закріплення вивченого матеріалу
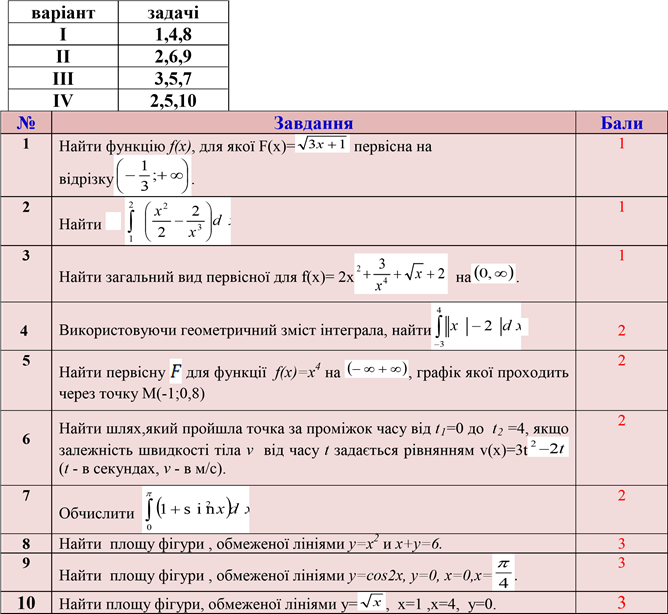
Самостійна робота по варіантам навчального характеру.
Таблиця варіантів
|
варіант |
задачі |
|
|||
|
І |
1,4,8 |
|
|||
|
ІІ |
2,6,9 |
|
|||
|
ІІІ |
3,5,8 |
|
|||
|
ІV |
2,7,10 |
|
|||
|
№ |
ЗАВДАННЯ |
БАЛИ |
||
|
1 |
Найдіть функцію f(x), для якої F(x)= cos3x-cosπ є первісною на . |
1 |
||
|
2 |
Обчислити інтеграл . |
1 |
||
|
3 |
Найдіть загальний вигляд первісної для функції 3 f(x)= s i n2 x + 4c o sx . |
1
|
||
|
4 |
5
−4 |
2 |
||
|
5 |
Найдіть первісну F(x) для функції f(x)=x2 на , графік якої проходить через точку М(-1;3). |
2 |
||
|
6 |
Найти закон руху точки, якщо швидкість прямолінійного руху точки змінюється за законом v(x)=3t 2−2t . |
2 |
||
|
7 |
Обчислити інтеграл . |
2 |
||
|
8
|
Найдіть площу фігури, обмежену лініями: y=2sinx, y= - sinx, 0≤ x ≤π |
3 |
||
|
9 |
|
3 |
||
|
10 |
Найдіть площу фігури, обмежену лініями: y=x2 , x+y=6, y=0. |
3 |
||
![]() Інтерактивні технології - робота в малих групах
Інтерактивні технології - робота в малих групах
Робота в малих групах дає змогу набути навичок спілкування та співпраці.
Після об’єднання у малі групи ви повинні за короткий час (8-10 хв.) виконати завдання та представити результати своєї роботи .
Картка – завдання з друкованою основою
|
Рисунок |
Варіант |
Завдання |
|
1.Дана фігура обмежена графіками відомих функцій: y=x? і y=x? Згадайте формули цих графіків функцій та знайдіть:
|
І варіант |
Знайти площу криволінійної трапеції ОNCD |
|
ІІ варіант |
Знайти площу криволінійної трапеції ОMCD |
|
|
ІІІ варіант |
Знайти площу затушованої трапеції ОMCN |
VII. Рефлексія Учням пропоную висловитися з питання:
1.Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).
2.Чи отримали ви задоволення від власної праці?
3.Чи вичерпали ви свої можливості?
4.Що тобі сподобалось на уроці?
5.Порівняйте свої знання на початку уроку і в кінці
VIII. Домашнє завдання
§9, п.1-2 , контрольні запитання №1-7
задачі № 207(4,5),212 1.Підготувати цікаву інформацію про І. Ньютона та Г. Лейбніца.
2.Практичне завдання:
|
№ |
Завдання: |
||||
|
1 |
Довести, що функція F є первісна для функції f на R а) F(x) = 3x – x2, б) F(x) = x2 – sin2x – 1, f(x) = 3 – 2x. f(x) = 2x – 2cos2x. |
||||
|
2 |
Найти загальний вигляд первісної для функції: x 1
|
||||
|
3 |
Для функції f найти первісної F, яка приймає дане значення в відповідній точці: 3
|
УРОК № 5 ТЕМА «ВИЗНАЧЕНИЙ ІНТЕГАЛ І ЙОГО ВЛАСТИВОСТІ»
I. Повторення теоретичного матеріалу проведемо у вигляді розв´язування кросворду
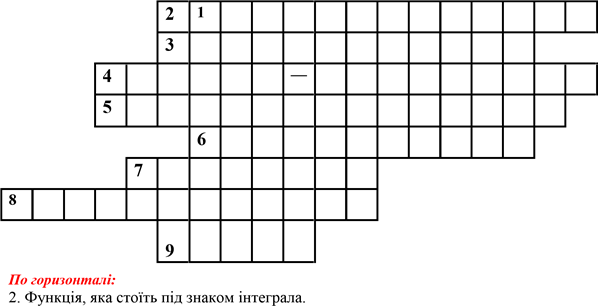
3. Операція знаходження первісних.
4. Вчені, які знайшли формулу для обчислення площі криволінійної трапеції. 5. Інтерпретація основної властивості первісної.
6. Назва функції F(x) для f(x).
7. Сукупність всіх первісних.
8. Величини, які знаходять з допомогою визначеного інтеграла.
По вертикалі
1.Тема, яку вивчаємо
II. Перевірка домашнього завдання:
МЕТОД «НАВЕДИ ПОРЯДОК »
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.
|
№ |
РОЗВЯЗУВАННЯ ЗАВДАНЬ:
|
||||||||
|
1 |
Довести, що функція F є первісна для функції f на R |
||||||||
|
а) б) |
|
|
|||||||
|
F′(x) = (x2 − s 2xi −1n)′ = ⊗x − 2c ⊗ ox |
|
||||||||
|
2 |
Найти загальний вигляд первісної для функції: |
||||||||
|
а) б в) |
|
|
|||||||
|
) |
|
|
|||||||
|
F |
|
||||||||
|
3 |
Для функції f найти первісної F, яка приймає дане значення в відповідній точці:
|
||||||||
|
б) |
F |
|
|||||||
Встановити відповідність:
(Кожна правильна відповідь оцінюється в один бал)
|
1 |
4
1 |
Т |
π4 − 3
|
|
2 |
|
Н |
|
|
3 |
π ∫ (x2 + 2s i nx)d 0 |
Ь |
3 547 |
|
4 |
|
Ф |
4,5 |
|
5 |
2 d x
|
О |
4 |
|
6 |
3π dx
0 cos 9 |
Ю |
|
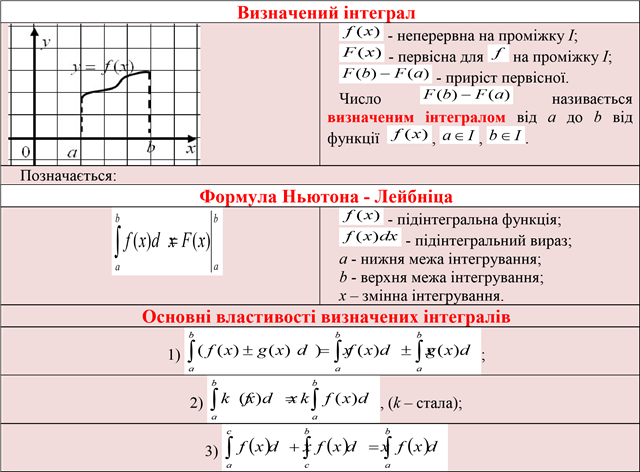
III. ТЕОРЕТИЧНИЙ МАТЕРІАЛ
III. Актуалізація опорних знань, умінь і навиків.
Інтерактивні технології
![]()
«Ажурна пилка» КАРТКА ДЛЯ ГРУПИ №1( Додаток №2 )
|
Рівн і |
|
ЗАВДАННЯ |
|
Бали |
|
2 |
= |
1.Доведіть, що функція: F(x) = s i n2 x +1 є первісною для функці sin2x, якщо х ∈ R. |
ї |
1 |
|
2.Знайти загальний вигляд первісної для функції: а) f (x) = |
|
2 |
||
|
3 |
|
3.Розв’язати задачу: - швидкість прямолінійного руху точки змінюється за законом υ(t) = 3t 2 − 2t . - Знайти закон руху точки, якщо при t=1 c x(t)=4м (2 бали). |
: |
1 |
|
а) ∫ 3 1 |
|
2 |
||
|
4 |
|
|
|
3 |
КАРТКА ДЛЯ ГРУПИ №2
|
Рівні |
ЗАВДАННЯ |
БАЛИ |
||
|
2 |
1.Доведіть, що функція: F(x) = x32 +1 є первісною для функції f (x) = − 63 на проміжку (−∞;0). x |
1 |
||
|
2.Знайти загальний вигляд первісної для функції: |
2 |
|||
|
|
|
а) f (x) = x − x42 ; б) f (x) =1+ 13 s i n3x . |
|
|
|
3 |
б |
3.Розв’язати задачу: - швидкість прямолінійного руху точки змінюється за законом υ(t) =1 0−t 2 . - Знайти закон руху точки, якщо при t=3 c x(t)=8м. |
: |
1 |
|
4.Обчислити інтеграл:
а) d x; б)
4 |
|
2 |
||
|
4 |
|
5. Обчислити площу заштрихованої фігури:
|
|
|
КАРТКА ДЛЯ ГРУПИ №3 Картка для більш підготовлених учнів.
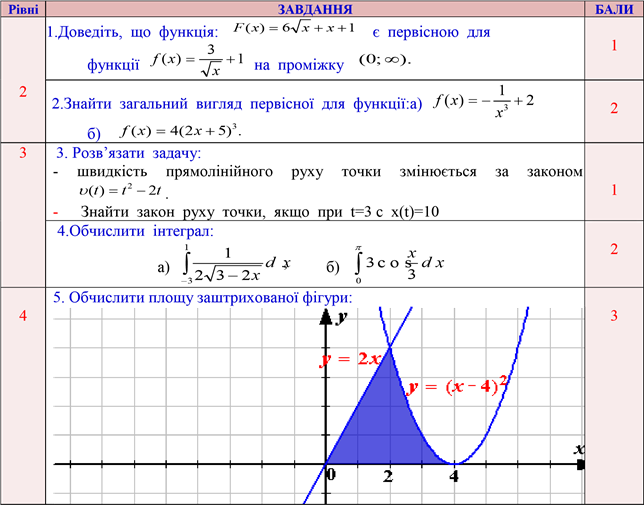
Інтерактивна вправа: « Знайди помилку»
1.
![]()
2.
![]() l∫4e−2nxd = − 12e−2x ll 34x= nn− 12(e−2l 4 − en −2l 3) =n− 12(el 11 −nel 91 )6=n − 12(11 − 19) = − 12(−617 ) =
27
l∫4e−2nxd = − 12e−2x ll 34x= nn− 12(e−2l 4 − en −2l 3) =n− 12(el 11 −nel 91 )6=n − 12(11 − 19) = − 12(−617 ) =
27
l 3 n

 Вправа «Рюкзак»
Вправа «Рюкзак»
Завдання
1.Відповісти на запитання
2.Скласти відповіді у рюкзак
Сьогодні на уроці
Я взнав:
1. _________________________________________
2.__________________________________________
3.__________________________________________
4.__________________________________________
5.__________________________________________ Я навчився:
1.____________________________________________
2.____________________________________________
3.____________________________________________
4.____________________________________________
5.____________________________________________
VI. Рефлексія
Учням пропоную висловитися з питання
1.Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).
2.Які пізнавальні процеси були задіяні на уроці найбільше (мислення, пам’ять, увага, уява)?
3.Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).
4.Чи отримали ви задоволення від власної праці?
5.Чи є бажання повторити свої відчуття?
VII. Домашнє завдання
§10, п.1-2 , контрольні запитання №1-4 задачі № 207(10,11);215.
1.Видатний учений Ісак Ньютон сказав: ,, У математичних питаннях не можна нехтувати й найменшими помилками “. Спробуйте знайти помилку у висловлюванні ( запис на дошці ). Один громадянин писав про себе: ,, Пальців у мене двадцять п’ять на одній руці, стільки ж на другій, на ногах десять…” Чому він такий потворний?
2.Практичне завдання:
|
Швидкість прямолінійного руху точки задається формулою: а)V(t) = t – 3t + 2.
б) v(t) =4 cos (3t - Написати формулу залежності її прискорення а і координати x від часу t в початковий |
||||
|
момент часу (t =0) і при t = |
|
, коли координата x = |
|
; х= - 5. |
2
УРОК № 6 ТЕМА «РОЗВ´ЯЗУВАННЯ ВПРАВ»
![]() I.ПЕРЕВІРКА
ДОМАШНЬОГО ЗАВДАННЯ
I.ПЕРЕВІРКА
ДОМАШНЬОГО ЗАВДАННЯ
Інтерактивна вправа « МІКРОФОН»:
Питання вправи:
1. Що називаємо первісною для функції f(x)?
2. Чи правда що F(x) = x2 є первісною для функції f(x) = 2x.
3. Яка теорема показує, як пов’язані між собою всі первісні даної функції?
1
4. Чи вірно, що первісна функції f(kx+b) дорівнює k F(kx+b)?
5. Що ми називаємо невизначеним інтегралом?
6. Яка первісна функції ех (F(x) = )?
7. Чи є функція F(x) = 3x2+x-2 первісною для f(x)=6х+1?
8. Чи є функція F(x) = 5 – 3x первісною для функції f(x) = –3 ?
9. Що являє собою загальний вигляд первісної для f(x) = ?
10. Чи вірно, що ![]() +
C
+
C
МЕТОД «МЕТЕОРИТНИЙ ДОЩ»
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.
|
№ Завдання |
Рішення |
|
Відповідь |
|||||||||||||
|
207(10) |
Знаходимо межі інтегрування: x =3 x , x3 = x2 , x2(x −1) = 0 x1 = ⊗, x2 = ⊗ , тоді
0 |
|
S= |
|
|
|||||||||||
|
|
||||||||||||||||
|
207(11) |
Знаходимо межі інтегрування: |
|
|
S = 4 1 2 |
|
|||||||||||
|
|
|
,тоді |
||||||||||||||
|
|
||||||||||||||||
|
S= |
1 ∫(2 − x − x2)d −2 |
x= |
⊗ 2 3 |
2 − 1 − 1 + 4 + 2 − 8 = ⊗ 2 3 3 |
||||||||||||
|
215 |
Якщо |
|
|
|
|
C |
|
|||||||||
|
дорівнювати: |
||||||||||||||||
|
|
||||||||||||||||
|
|
1 |
|
||||||||||||||
|
||||||||||||||||
 САМОСТІЙНА РОБОТА
САМОСТІЙНА РОБОТА
ВИКОРИСТОВУЮЧИ ТВЕРДЖЕННЯ, ПЕРЕВІР СЕБЕ
|
|
Рівні |
|
|
Завдання |
|
|
Бали |
|
|
1 |
|
1. Побудуйте схематично фігури, площі яких виражаються такими інтегралами:
11
|
|
3 |
||||
|
2 |
|
3. Запишіть за допомогою інтеграла площі фігур, зображених на малюнках (а-г):
|
|
3 |
||||
|
3 |
|
3. Знайти первісну функцій, що задовольняють дану умову:
F(1) = 0 ;
F(0) = 0. |
|
3 |
||||
II. Приклади розв’язування задач (з послідовним коментарем)
Завдання 1
Знайти всі первісні функції f1(x) = x2 , графіки яких дотикаються параболи f2(x) = x2 +1.
Рішення.
В точці дотику F(x) =f2(x) і f1(x) = f2′(x) (за визначенням дотичної)
F(x) = - загальний вигляд первісної для функції f1(x): f2′(x) =2x і x2 = 2x, звідки x =0 або x =2.
1) x=0, C=1 отримаємо F1(x) =
2) x =2 , , C = отримаємо F2(x) = .
Відповідь: F1(x) = , F2(x) = .
Завдання 2
Для функції f(x) = s i n2 x +
c o2 x +s![]() s i
n3x знайти первісну , графік якої проходить через точку
s i
n3x знайти первісну , графік якої проходить через точку
А (π![]() 6 ;
6 ;![]() ) .
) .
Рішення.
Перетворимо
функцію f(x) = 1 + ![]() sin3x
. Тоді F(x) = x -
sin3x
. Тоді F(x) = x - ![]() c
o s3x + C
c
o s3x + C ![]() −
− ![]() c o
c o![]() +s C =
+s C =
![]() , C = 0 отримаємо F(x) = x −
, C = 0 отримаємо F(x) = x −
![]() c
o s3x .
c
o s3x .
Відповідь:
F(x) = x −
![]() c
o s3x
c
o s3x
![]() ІII. Актуалізація опорних знань, умінь і навиків.
ІII. Актуалізація опорних знань, умінь і навиків.
Самостійна робота по варіантам навчального характеру.
Таблиця варіантів
САМОСТІЙНА РОБОТА:
МЕТОД «ІНТЕЛЕКТУАЛЬНИЙ ВИХОР» Робота в малих групах дає змогу набути навичок спілкування та співпраці. Після об’єднання у малі групи ви повинні за певний час (15 хв.) виконати завдання та представити результати своєї роботи .
Правила роботи в малих групах див. Додаток № 1
КАРТКА ДЛЯ ГРУПИ №1
|
№з\п |
ЗАВДАННЯ |
БАЛИ |
|
|
2 |
1. Доведіть, що функція: F(x) = с o−s i ns x2x −7 є первісною для функції f (x) =−s i nx −2c o2x на проміжку (−∞;∞). |
1 |
|
|
2. Знайти загальний вигляд первіс а) f |
ної для функції: б) f |
2 |
|
|
3 |
3. Розв’язати задачу: - швидкість прямолінійного руху - Знайти закон руху точки, як |
точки змінюється за законом: υ(t) = 4t3 − 4 що при t=2 c x(t)=7м. |
1 |
|
б 4.Обчислити інтеграл: а)
|
2 |
||
|
4 |
5. Обчислити площу заштрихованої фігури:
|
3 |
|
КАРТКА ДЛЯ ГРУПИ № 2 Картка для більш підготовлених учнів.
|
№з\п |
ЗАВДАННЯ |
БАЛИ |
|
2 |
1.Доведіть, що функція: є первісною для функції на проміжку |
1 |
|
2.Знайти загальний вигляд первісної для функції: а) б) |
2 |
|
|
3 |
3.Розв’язати задачу:швидкість прямолінійного руху точки змінюється за ном: . Знайти закон руху точки, якщо при t=2 c x(t)=5 м |
1 |
|
б 4. Обчислити інтеграл: а) б) |
2 |
|
|
4 |
5. Обчислити площу заштрихованої фігури: |
3 |
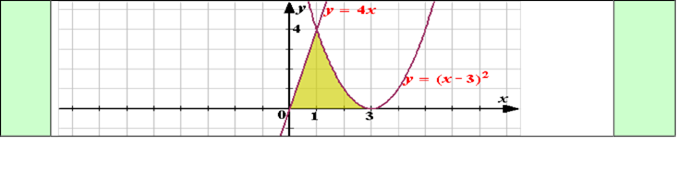
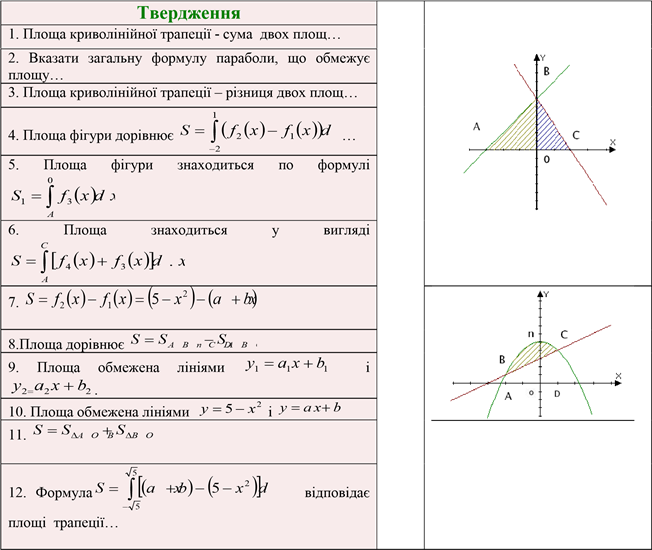
ВПРАВА «ВСТАНОВИ ВІДПОВІДНІСТЬ»
Виберіть правильне твердження для кожної фігури, з'єднайте прямими у відповідності до малюнка.
VI.Рефлексія
Учням пропоную висловитися з питання
1. Що тобі сподобалось на уроці?
2. Що ти хотів би змінити під час уроку?
3. Порівняйте свої знання на початку уроку і в кінці.
4. Які пізнавальні процеси були задіяні на уроці найбільше (мислення, пам’ять, увага, уява)?
5. Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).
V.Домашнє завдання
§10, п.1-2 , контрольні запитання №1-4 задачі № 200(6-9),204(1-2)
1.Практичне завдання:
|
ЗАВДАННЯ |
|||||||||
|
1. Побудуйте схематично фігури, площі яких виражаються такими інтегралами:
|
a) в) |
|
; б) xdx; r) |
|
; . |
||||
|
0 |
3 dx ∫ x 1 |
||||||||
|
2. Знайти первісну функцій, що задовольняють дану умову:
|
1) 2) 3) 4) |
|
|
||||||
|
|
; |
||||||||
|
;
|
|||||||||
|
|
|||||||||
|
|||||||||
УРОК № 7 ТЕМА «ЗАСТОСУВАННЯ ІНТЕГРАЛА»
I. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
Повторимо теоретичний матеріал, розгадавши кросворд.
Кросворд
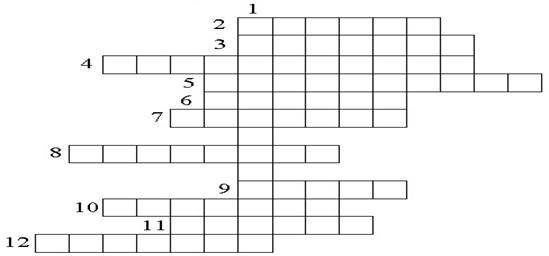
1.Ключове слово: як називається функція F(x)?
2. Що є графіком функції у = ах+b?
3. Найменша учнівська оцінка.
4. Який урок звичайно проходить до заліка? 5. Синонім слова дюжина?
6. Він є в кожному слові, у рослин і можливо є в рівнянні .
7. Що можливо розрахувати за допомогою інтеграла?
8. Одне із важливих понять математики.
9. Форма урока, на якому проводять перевірку знань.
10.Німецький вчений, в честь якого названа формула, що з’єднує площу криволінійної трапеції і інтеграл.
11. Множина точок площини з координатами (x, f(x)), де х пробігає область визначення функции f.
12.Відповідність між множинами Х и Y, при якій кожному значенню із множени Х поставлено в відповідність одне значення із множени Y, носить назву ....
Метод « Метеоритний дощ »
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.
|
ЗАВДАННЯ |
|||
|
1. Знайти первісну функцій, що |
1) 2) 3) 4) |
⊗ |
, |
|
F(x)=⊗ 2x−1+⊗
|
|||
ІНТЕРАКТИВНА ВПРАВА «МОЗКОВИЙ ШТУРМ»
|
№з\п |
Завдання |
Бали |
|
1 |
Похідна функції F(x) дорівнює 2х. Знайдіть функцію F(x). |
1 |
|
2 |
Знайдіть загальний вид первісних для функцій: а) y=2; б) y=-5x+3; в) y=2(4x+1); г) y=3x. |
1 |
|
3 |
а) y= x2 б) y=3x2 +2x в) y=x−3x3 г) y=x2 −5x4 |
1 |
|
4 |
а) y=sin x; б) y=3sin
x; в) y =
c o s
x −π |
1 |
|
5 |
а) y= (x−2)4 б) y=(2x+5)5 в) y= (2−7x)1 0 г) y=2(2x+5)4 |
1 |
|
6 |
|
1 |
|
7 |
Швидкість прямолінійного руху точки змінюється за законом v(t) = 3t 2 − 2t . Знайдіть закон руху точки. |
1 |
|
8 |
Тіло рухається по прямій зі швидкістю v(t) = 4t + 2 (t – час у секундах, v – швидкість у метрах за секунду). Знайдіть довжину шляху, пройденого тілом за перші 3 с. |
1 |
|
9 |
Знайдіть шлях, пройдений точкою за перші 5 с, якщо швидкість точки змінюється за законом v(t) =1 0− 2t (t – час у секундах, v – швидкість у метрах за секунду). |
1 |
|
10 |
Обчисліть інтеграли: а) ∫ 0 |
1 |
|
11 |
Обчисліть площу фігури, обмеженої лініями y=x, y=0 і x=3. |
1 |
|
12 |
Обчисліть площу фігури, обмеженої лініями y=2x, x=a та x=b, де a>0, b>a. |
1 |
ВЗАЄМОПЕРЕВІРКА- 5 хвилин
Учням пропонується після розв’язання прикладів помінятися зошитами і перевірити самостійну роботу у сусіда по парті за зразком, який буде спроектовано на екрані. Оцінку за роботу поставити в зошит та лист самооцінки відповідно до критеріїв оцінювання.
ПЕРЕВІРНА РОБОТА №1
|
Варіант №1 |
Варіант №2 |
||
|
Найти визначений інтеграл: |
|||
|
|
|
;
|
|
|
Варіант №3 |
Варіант №4 |
|
|
|
Найти визначений інтеграл: |
|||
|
1)
∫ 0 π
4 2) ∫s i n2x ⋅c o s2x d ; 0
3) d x. |
0 1)
2) ∫ 2cos2 3xdx; 3) d x. |
||
![]()
Робота в малих групах.
Робота в малих групах дає змогу набути навичок спілкування та співпраці.
Після об’єднання у малі групи ви повинні за певний час (10 хв.) виконати завдання та представити результати своєї роботи .
ПЕРЕВІРНА РОБОТА №2.
Гра « ХТО ШВИДШЕ »
Варіант – 1
|
Рівень |
Завдання |
Бали |
|
1 |
а) f; б) f (x) = 3x 2 +1в) f (x) = 4(2х + 5)3. |
3 |
|
2 |
2
1 0 cos 1 1 d x;
|
3 |
|
3 |
3. Знайти площу фігури, обмеженої лініями: 2 а) у = х +1, у = 0, х = - 1, х = 2. б) у = 4 – х2 і у = х + 2. |
3 |
Варіант – 2
|
Рівень |
Завдання |
|
Бали |
|
1 |
1 . Найти загальний вид первісних для функцій 1 3 3 в) f (x) =− 32 + x32
|
|
3 |
|
2 |
0 |
d x; |
3 |
|
3 |
3. Знайти площу фігури, обмеженої лініями: а) у = -х2+1, у = 0, х = -2, х =1. б) у = 4 + х2 і у = х -2. |
|
3 |
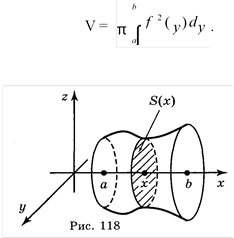
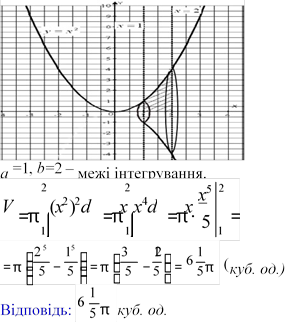
II. ТЕОРЕТИЧНИЙ МАТЕРІАЛ ЗАНОТУЙ В ЗОШИТ!
|
Обчислення об’ємів за допомогою визначеного інтеграла |
|||||||||||||
|
Внаслідок обертання цієї криволінійної трапеції навколо осі Ох утворилося тіло, об’єм якого можна обчислити за формулою: b
a Обчислення об’єму тіла, утвореного обертанням графіка функції навколо вісі Оу:
|
x =1, x = 2. Розв’язання y = 0 - вісь Ох; x =1 - пряма, що проходить через точку
(2;0) паралельно осі Оу; y= x2 - парабола.
|
||||||||||||
ІII. Мотивація навчальної діяльності
Розглянемо використання поняття інтеграла в інших галузях.
Поняття інтеграла – важливе як у шкільному курсі математики, так і в курсі вищої математики, що розгалужується на низку цікавих, хоч і складних, математичних дисциплін.
Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні, оскільки необхідні для ведення різноманітних справ, для гармонійного розвитку галузей виробництва, тощо.
У цих науках також використовується поняття інтеграла. Серед них такі як :
- економіка виробництва, - фізика,
- фінансова справа, - хімія,
- електроніка, - радіофізика, тощо.
- програмування,
Давайте з'ясуємо, як саме ми можемо застосувати визначений інтеграл в таких науках, як геометрія, фізика, економіка.
Зараз давайте «перенесемося в майбутнє», років на 20 вперед. Ви – дорослі, солідні люди, знайшли своє місце в житті: конструктори, інженери, металурги, будівельники, економісти, плановики, вчені. І в процесі своєї роботи ви зустрічаєтеся з різними проблемами, які вам необхідно вирішити. Розіб’ємо клас на 4 групи, кожна з яких отримує певне завдання і через 5 хвилин звітує про виконану роботу.
Фінансисти
![]() На полі пшениці після приземлення космічного
корабля залишився слід, який нагадує фігуру, обмежену
лініями у =│х2 – 2х - 8│ та у = 3 + │х - 1│. Необхідно визначити збитки,
завдані агрокомплексом, якщо з 1 м2 отримують в середньому 3,8 кг пшениці, яка
коштує 0,8 грн. / кг Розв’язання:
На полі пшениці після приземлення космічного
корабля залишився слід, який нагадує фігуру, обмежену
лініями у =│х2 – 2х - 8│ та у = 3 + │х - 1│. Необхідно визначити збитки,
завдані агрокомплексом, якщо з 1 м2 отримують в середньому 3,8 кг пшениці, яка
коштує 0,8 грн. / кг Розв’язання:
S =2∫3 (−(x2 −2x +8)−(3+(x −1)))d +
1
![]()
![]() d =
d =
4 1 3 4
![]()
![]()
![]() = 2 x3 x2 6x13+ x33 − x22 − 6x34−− x33 + x22 +1 x54 = 20⋅ 43 = 2 23 (Μ0 2)
= 2 x3 x2 6x13+ x33 − x22 − 6x34−− x33 + x22 +1 x54 = 20⋅ 43 = 2 23 (Μ0 2)
− + +
3 2
B![]() (грн) Відповідь.
81,07 грн.
(грн) Відповідь.
81,07 грн.
Археологи
Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = – х2 + 2х + 3 навколо вісі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м3. Яка масу каменя використали на виготовлення цього жертовника стародавні майстри?
![]() Розв’язання.
Побудуємо фігуру, обмеженою параболою у = – х2 + 2х + 3,
осями Оу та Ох.
Розв’язання.
Побудуємо фігуру, обмеженою параболою у = – х2 + 2х + 3,
осями Оу та Ох.
Об’єм тіла, яке утворюється внаслідок обертання графіка функції навколо oсі Ох обчислюється за
b
формулою: V =π∫ f 2(x)d x.
a
V =π∫3 (−
x2 +2x+3)2d = ∫3 (x4 −4xx3 −2x2 +1 x+9)d =π2x55 − xx4 +
2x3 +6x2 +9x![]() 03 ==
03 ==
0 0 3
3,14⋅(4 ,6 − 8 8−1 +15 +82 )4= 3,17 ⋅3 ,64= 90,0 (M6 3 )8
m =V ⋅ p m = 9 ,0 6 ⋅28 54= 2 0 4 (0Κ0) Відповідь. 240210 кг.
Фізики
Для кращого обслуговування заїзду гонок серії "Формула-1" майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 2·(t+2)5/2. Який шлях проїде пілот цієї гонки за 7 с від початку руху? Який шлях він проїде за сьому секунду?
![]()
![]()
![]() Розв’язання:s(7)=∫7 2(t +2)25 74 t +t 2)72 = (2 −8 12)=1 8(m) d = (
Розв’язання:s(7)=∫7 2(t +2)25 74 t +t 2)72 = (2 −8 12)=1 8(m) d = (
0
d = (
s(7)=∫7 2(t +2)25 74 t +t2)7276 =74(2 −1 1 2)=048 (m) Відповідь 1243 м; 422 м.
6
Біологи
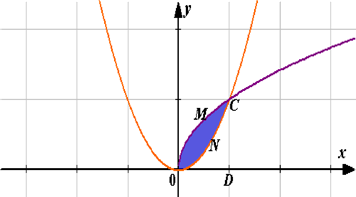
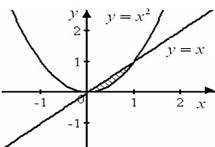
Знайти площу пелюстка ромашки, який розміщено між дугами параболи
![]()
![]() y = x2 y = x
y = x2 y = x
Розв’язання: Дана фігура обмежена графіками двох функцій: y = x2 та y= x , шукана площа за допомогою інтеграла
![]() 1
1
12
![]()
![]() обчислюється так:S = ∫x − x2d
=
2xx332 − x33 10=
23 − 13
= 13(k
.o )Відповідь.
1/3 кв. од.
обчислюється так:S = ∫x − x2d
=
2xx332 − x33 10=
23 − 13
= 13(k
.o )Відповідь.
1/3 кв. од.
0
![]() Вправа «Прес» – відповісти на запитання за схемою:
Вправа «Прес» – відповісти на запитання за схемою:
«Я вважаю, що …»
«Тому що …» «Наприклад …» «Отже …».
1. Первісною для функції f(x) називаємо функцію F(x) …
2. … F(x) = x2 є первісною для функції f(x) = 2x.
3. Як пов’язані між собою всі первісні даної функції?
1
4. Первісна функція f(kx+b) дорівнює k F(kx+b), тому …
1. …первісна функції ех дорівнює F(x)=
2. Функція F(x) = 3x2+x-2 є первісною для f(x)=6х+1, … 3. Функція F(x) = 5 – 3x є первісною для функції f(x) = –3,…
4. Що являє собою загальний вигляд первісної для f(x) = ?
5. Чи
вірно, що ![]() +
C , тому…
+
C , тому…
ІV. Узагальнення та систематизація знань, вмінь та навичок.
Встановити відповідність:
|
№ |
ЗАВДАННЯ |
|
|
|
1 |
Обчислення площі криволінійної трапеції Поставте правильно напрямок від фігури до формули, завдяки якій можна обчислити її площу. |
|
|
|
а |
|
b b S = ∫ f (x)d −x∫ g(x)d a c
|
1 |
|
б |
|
b c S = ∫ f (x)d +x∫ g(x)d a b
|
1 |
|
в
|
|
b S = ∫( f (x) − g(x) )d a |
1 |
|
г |
|
b S = ∫ f (x)d x a
|
1 |
|
д |
|
b S = −∫ f (x)d x a |
1 |
|
2 |
Застосовування інтеграла у фізиці Поставте правильно у відповідність формула – фізична величена |
|
|
|
а |
b А = ∫ F(x)dx a |
Швидкість тіла |
1 |
|
б |
t2 А = ∫N(t)dt t1 |
Заряд |
1 |
|
в |
t2 х = ∫v(t)dt t1 |
Роботу при прямолінійному русі |
1 |
|
г |
t2 v = ∫а(t)dt t1 |
Кількість теплоти |
1 |
|
д |
т = dx |
Робота при змінній потужності
|
1 |
|
є |
t2 q (t) = ∫І(t)dt t1 |
Координата тіла
|
1 |
|
ж |
t2 Q = ∫с(t)dt t1 |
Маса стержня |
1 |
![]() Робота в малих групах.
Робота в малих групах.
Робота в малих групах дає змогу набути навичок спілкування та співпраці.
Після об’єднання у малі групи ви повинні за певний час (10 хв.) виконати завдання та представити результати своєї роботи .
Варіант 1
|
№ з\п |
Завдання |
Варіант відповіді |
Бали |
|
1 |
Множина первісних для функції: f (x) = 6x має вигляд: |
а) F(x) = 6x +C ;б) F(x) = 6x l n6+C ; 6x C ; г) F(x) = 5x + C ; в) F(x) = + l n6 l n5 |
1 |
|
2 |
Знайти загальний вигляд первісних для функції: y=x2 +1.
|
x3 x3 x3 а) + C ;б) +1+C ;в) + x +C ; 3 3 3 г) x3 + x+C . |
1 |
|
3 |
Обчислити інтеграл: . |
а) 8; б) 16; в) 24; г) -8. |
1 |
|
4 |
Графік якої з первісних функції: f (x) = 2x3 проходить через точку А (2;1) ? |
x4 7; б) F(x) = x4 + 7 ; а) F(x) = − 2 4 в) F(x) = x 4 −7; г). F |
1 |
|
5 |
Знайти множину всіх первісних для функції: f (x) = 3x 2 + 4x −1. |
а) F(x) = 6x+ 4;б) F(x) = x3 + 2x 2 − x ; в) F(x) = 3x3 + 4x 2 − x;г) F(x) = 6x3 + 4x 2 − x ; |
1 |
|
6 |
Швидкість тіла, що рухається прямолінійно, виражається формулою v(t) = 5t 4 −3t 2 + 2. В початковий момент тіло перебувало у початку координат. Якою формулою виражається залежність координати х від часу t? |
а) x(t) = t 3 −t 2 + 2 ; б) x(t) = 2 0t 3 −6t +t ; в) x(t) = t 5 −t 3 + 2t ; г) x(t) = 2 t53 −9t 2 + 2t .
|
1 |
|
7 |
Яка із формул виражає площу заштрихованої фігури?
|
а) d x;б) ∫(x2 −1)d x; в) |
1 |
|
8 |
. Яка з
формул відповідає обчисленню інтеграла:
|
π π π π 2 2 2 2
π π π π 3 3 3 3 |
1 |
|
9 |
Об’єм тіла при обертанні криволінійної трапеції, обмежено лініями y2 =4x ; x = 0 ; y = 0, дорівнює: |
а) 16π; б) 32π; в) 10π; г) 8π. |
1 |
Варіант 2
|
№ з\п |
Завдання |
Варіант відповіді |
Бали |
|||||
|
1 |
Множина первісних для функції: f (x) = 2c o sx має вигляд: |
а) F(x) = 2x+s i nx+C ;б) F(x) = 2+s i nx+C ; в) F(x) = 2x−s i nx+C ;г) F(x) = 2−s i nx+C |
1 |
|||||
|
2 |
Знайти загальний вигляд первісних для функції: y=8x2 . |
8x3 x3 а) +C ;б) +1+C ;в)8x +C ;г) x3 + x+C . 3 3 |
1 |
|||||
|
3 |
Обчислити інтеграл: . |
а) 27; б) 81; в) 9; г) 12. |
1 |
|||||
|
4 |
Графік якої з первісних функції: f (x) = x3 проходить через точку А (1;3) ? |
а) F(x) = 1 x3 + 2 3 ;б) F(x) = x3 − 2 3 ; 3 4 3 4
в) F |
1 |
|||||
|
5 |
Знайти множину всіх первісних для функції: f (x) = 13 +s i nx . x |
а) F(x) =− 14 −c ox+Cs ; 4x б) F(x) = 14 −c ox+sC ; 4x в) F г) F |
1 |
|||||
|
6 |
. Швидкість тіла, що рухається прямолінійно, виражається формулою v(t) = 2t 3 −3t 2 +3 . В початковий момент тіло перебувало у початку координат. Якою формулою виражається залежність координати х від часу t? |
а) x(t) = 6t 2 −6t ; б) x(t) = − 2
4
|
1 |
|||||
|
7 |
Яка із формул виражає площу заштрихованої фігури?
|
0
0
|
1 |
|||||
|
8 |
Яка з формул відповідає 2 інтеграла: ∫ x3dx . 1 |
обчисленню |
а)1 б) 3x 4 |
2 в) x4 1 |
2 1 |
г) 4 |
1 2 |
1 |
|
9 |
Об’єм тіла при обертанні трапеції, обмежено лініями y= y = 0, дорівнює: |
|
а) 18π; б) 9π; в) 36π; г) 8π.
|
|
|
1 |
||
Тестування.
Розв’язування тестових завдань "Перевір себе" 1. За якою з наведених формул визначається площа даної фігури?
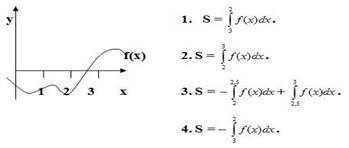
2.Знайдіть в яких записах є помилка.
![]()
![]()
![]()
![]() 5. ∫1 3x2d x= 9x1 ∫1 6x2d x= x31 ∫1 3x2d x=
x310 8. ∫1 6x7d x=
34x810
0 6. 20 7.
5. ∫1 3x2d x= 9x1 ∫1 6x2d x= x31 ∫1 3x2d x=
x310 8. ∫1 6x7d x=
34x810
0 6. 20 7.
0 0 0 0
3.За якою з наведених формул обчислюється робота змінної сили, заданої формулою F(x)= 3x2–4x+8, вздовж відрізка довжиною 2 м?
![]() 9. A
9. A ![]() d d
d d
2
11. A = (3x2 −
4x +
8)′
12. A ![]() d
d
0
4.За якою з формул обчислюється обсяг виготовленої за 4 години продукції, якщо
3?
продуктивність праці задається формулою f(x)= 4x
![]() . 14.
. 14.![]() . 15.(4x3)′
16.
. 15.(4x3)′
16.![]() .
.
5. В якому випадку вірно обчислено навантаження електростанції за 3 години, якщо її витрати визначаються функцією: f (x)= t84 + 7t ?
![]() d t 18. ∫(8t +7t)d t 19.
8 ′ 3
d t 18. ∫(8t +7t)d t 19.
8 ′ 3
0 4 t4 + 7t 20. ∫0 t84 + 7td t
6. В якому з наведених випадків вірно визначений середній час, витрачений на засвоєння одного виробу від 10 до 20 виробів, якщо функція t= 3х описує зміни витрат часу t на виготовлення виробів в залежності від степеня засвоєння виробництва.
21.tc e p![]()
![]() x d
22.tc e p
x d
22.tc e p![]()
![]() x d
x d
23.tc e p![]() x d 24.tc e p
x d 24.tc e p![]() x d
x d
0 1 0
Номера правильних відповідей закресліть у бланку відповідей.
|
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
|
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
|
V Рефлексія
Учням пропоную висловитися з питання
1. Порівняйте свої знання на початку уроку і в кінці.
2.Які пізнавальні процеси були задіяні на уроці найбільше (мислення, пам’ять, увага, уява)?
3.Чи отримали ви задоволення від власної праці?
4.Чи є бажання повторити свої відчуття?
5.Що тобі сподобалось на уроці? 6.Що ти хотів би змінити під час уроку?
VI Домашнє завдання
§11, п.1-2 , контрольні запитання №1-8 задачі № 207(4;5)210;213
УРОК №8 ТЕМА: «РОЗВЯЗУВАННЯ ЗАДАЧ»
I. Повторення вивченого матеріалу
РУБРИКА: «Я вже це знаю!» Відповісти на запитання:
- З яким важливим поняттям в алгебрі ми працювали на попередніх уроках?
- Що вам відомо про це поняття?
- Що називаємо первісною для функції f(x)?
- Чи правда що F(x) = x2 є первісною для функції f(x) = 2x.
- Яка теорема показує, як пов’язані між собою всі первісні даної функції?
1
- Чи вірно, що первісна функції f(kx+b) дорівнює k F(kx+b)?
- Що ми називаємо невизначеним інтегралом?
- Що являє собою загальний вигляд первісної для f(x) = ? - Яка первісна функції ех (F(x) = )?
- Чи є функція F(x) = 3x2+x-2 первісною для f(x)=6х+1?
- Чи є функція F(x) = 5 – 3x первісною для функції f(x) = –3 ?
Інтерактивна вправа « Мозковий штурм»
1. «Знайди помилку»: чи вірно, що:
а) ∫x5d x= 5x4 +C ; б)![]()
![]() x7
x7
2. Перевір, чи вірні рівності:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() x ;
x ;
![]()
![]() 3 5x23 5
3 5x23 5
г) ∫5d = x2= 2 (32 −02) = 42 ; д) ∫10 x2d =xx3310 = 13(1−0) = 13
00
3. «Сам собі режисер »: знайди первісні для функцій:
x
а) f(x) =10х; б) f(x) = х²; в) f(x) =-sin(2x); г) f(x) = 5cosx; д) f(x) = 6х²; е)f(x) = 3tg 3
4. Знайди за допомогою інтеграла площу фігури, намилювану на рисунку:
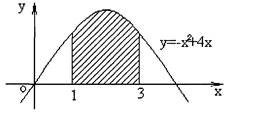
5.Записати за допомогою інтеграла формулу, за якою знаходиться площа затушованої фігури:
а) б) в)
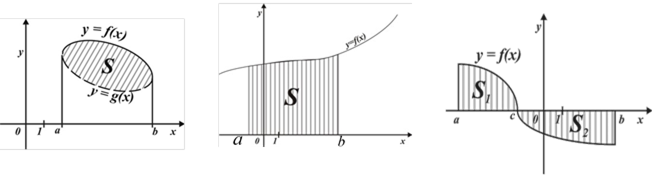
6.Заповнити в таблицю:
|
1) Формула Ньютона – b Лейбніца:∫ f (x)dx = a |
Якщо функція непарна, тоді: |
|
|
b 2) ∫( f (x)+ g(x))d x= a |
∫xnd x= 1. n≠−1. |
1. ∫(k x+ b)nd x= n ≠−1. |
|
b a 3) ∫ c f(x)d x= 4) ∫ f (x)d x= a a |
2. ∫xd x= |
2. ∫(k x+b)d x= |
|
c b 5) ∫ f (x)d +x∫ f (x)d =x a c |
|
3. |
|
6)Якщо функція парна , тоді a ∫ f (x)d x= −a |
|
|
|
7)Якщо функція непарна, тоді a ∫ f (x)d x= −a |
5. ∫s i nxd x= |
5. ∫s i n(k x+b)d x= |
|
|
6. ∫c o sxd x= |
6. ∫c o(k xs+b)d x= |
|
|
|
|
II.ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
Метод «Метеоритний дощ»
Записуємо на дошці розв’язання домашніх вправ з пропусками. Два учні заповнюють пропуски і пояснюють хід міркувань. Під час розгляду розв’язання завдань зошити в учнів закриті. Після закінчення пояснення учні відкривають зошити, кожен перевіряє свою роботу за зразком, підкреслює помилки.
|
№ завдання |
Рішення |
|
207(4) |
π π S =
∫(2s x −
⊗i)d =
n∫⊗
d x=
− ⊗ 0 0 |
|
207(5) |
Знаходимо межі інтегрування: x2 +x− 2 = 0, x1 =⊗, x2 =−2, тоді
S= 2 2 − ⊗ 2= 8- 2 − 2 |
|
213 |
1 1 1 |
|
210 |
|
III. Мотивація навчальної діяльності.
Перевір себе! ІНДИВІДУАЛЬНА РОБОТА
«ТЕСТ»
|
№ |
Завдання |
Варіант відповіді |
Бал |
||
|
1 |
Множина первісних для функції: f (x) = 2+s i nx має вигляд: |
а) F(x) = 2x−c ox+sC ;б) F(x) = 2x+c ox+sC ; в) F(x) = 2+c ox+sC ;г) F(x) = c ox−s2+C ; |
|
1 |
|
|
2 |
Знайти загальний вигляд первісних для функції: y=5x4 . |
3 x5 а) 20x +C ; б) +C ;в) x5 +C ; г) 4x5 +C . 5 |
|
1 |
|
|
3 |
0 Обчислити інтеграл: ∫exdx . −1 |
1 1 1 а) − ; б) 1− ; в) 1− e ; г) −1. e e e |
|
1 |
|
|
4 |
Графік якої з первісних функції: f (x) = x 4 проходить
через точку А ? |
а) F в) F |
|
|
1 |
|
5 |
|
FC ;в) F г) F(x) =−c (t g3x−2)+C ; |
|
C ; |
1 |
|
6 |
Швидкість тіла, що рухається прямолінійно, виражається формулою v(t) = 4t 2 −3t 2 + 2 . В початковий момент тіло перебувало у початку координат. Якою формулою виражається залежність координати х від часу t? |
а) x(t) =1 2t 2 + 6t ;б) x(t) = t 4 −t 3 + 2t ;
в) x(t) =1 t64 −9t 2 + 2t ;г) x(t) = t 4 −t 2 + 2 .
|
|
|
1 |
|
7 |
Яка із формул виражає площу заштрихованої фігури?
|
0
в) |
. |
|
1 |
|
8 |
Яка з формул відповідає обчисленню інтеграла:
|
22 |
1 |
||
|
9 |
|
а) 8π; б) 16; в) 16π; г) 32π.
|
1 |
||
ІII. Актуалізація опорних знань, умінь і навиків.
![]() Дидактична гра
Дидактична гра
Правила гри
Учні об’єднуються у чотири команди.
|
2. Обчислити інтеграли: 2) |
|
;
|
|
|
![]() Ігрове поле складається з
розмальованого планшета, на якому зображено гору з нанесеним на неї
маршрутом сходження та зупинками. Зупинки пронумеровані, старт позначено
прапорцем. Команди з головуючим займають старт — початкову позицію. На кожній
зупинці викладач перевіряє правильність виконання завдання. Виграє та команда,
яка більше набере балів за швидко і правильно виконані завдання і підніметься
на „ вершину знань ”. Розщілина „ Графічна ”.
Ігрове поле складається з
розмальованого планшета, на якому зображено гору з нанесеним на неї
маршрутом сходження та зупинками. Зупинки пронумеровані, старт позначено
прапорцем. Команди з головуючим займають старт — початкову позицію. На кожній
зупинці викладач перевіряє правильність виконання завдання. Виграє та команда,
яка більше набере балів за швидко і правильно виконані завдання і підніметься
на „ вершину знань ”. Розщілина „ Графічна ”.
Плато „ Криволінійна трапеція ”.
Завдання:
 3. Обчислити площу фігури, обмеженої лініями:
3. Обчислити площу фігури, обмеженої лініями:
|
4.Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої:
1) графіком функції y=4x та прямими х=9, у=0; 2) косинусоїдою y=cos x та прямими х=9, , у=0; 3) прямими у=2х, х=0, у=5; |
|||||
|
4) кривою |
y= x3 |
і прямими х=1 і х=2. |
|||
Результати дидактичної гри:
хто дійшов до десятичної вершини „ Об’ємного успіху ”, той одержує
знак
„ Майстер математичного аналізу ”.
VI. Рефлексія Учням пропоную висловитися з питання:
1.Розвитку яких рис характеру сприяв урок (самостійності, спостережливості, відповідальності).
2.Які пізнавальні процеси були задіяні на уроці найбільше (мислення, пам’ять, увага, уява)?
3.Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).
4.Чи отримали ви задоволення від власної праці? 5.Чи є бажання повторити свої відчуття?
VII. Домашнє завдання
§11, п.2 , контрольні запитання №1-3
задачі № 214;217
Практичне завдання: розгадати кросворд
Питання кросворда
1. Перша буква якого слова нагадує знак інтеграла?
2. Хто з відомих математиків фізиків дослідив фізичний зміст інтеграла?
3. Хто з відомих математиків дослідив математичний зміст інтеграла?
4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла?
5. Як називається функція яка стоїть під знаком інтеграла?
6. Як називається множник dx у підінтегральному виразі? 7. Як називається операція, обернена до операції диференціювання?
УРОК №9 ТЕМА: «РОЗВЯЗУВАННЯ ЗАДАЧ»
I. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ
Завдання уроку: повторити визначення і формули первісної і інтеграла, вирішити вправи на застосування цих формул, підготуватися до тематичної атестації.
ДЕВІЗ УРОКУ: «ГОВОРИ, ЩО ЗНАЄШ, РОБИ, ЩО ВМІЄШ, ПРИ ЦЬОМУ ПАМЯТАЙ: ЗНАТИ І ВМІТИ БІЛЬШЕ НІКОЛИ НЕ ШКІДЛИВО»
![]()
II.ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
Метод «Інтелектуальний вихор» (групова форма роботи)
Клас поділити на чотири групи. Кожна група отримує завдання, які подібні до тих, що треба було розв’язати вдома і працює над карткою 10 хвилин.
Завдання: І. Початковий рівень
|
1. Знайти площу фігури, обмеженої лініями: 2.
|
|
; |
|
; |
|
; |
|
. А(1;2). |
|||
|
знайти первісну, графік якої проходить через точку |
|
|
|
||||||||
|
3. Обчислити інтеграл |
2 ∫ x2dx 1 |
. |
|||||||||
|
|||||||||||
Завдання: ІІ. Середній рівень
|
4. Знайти загальний вигляд первісних для функції 5.
6. Знайти площу фігури, обмеженої лініями:
|
|
. , графік якої проходить через точку
|
|
|
Завдання: ІІІ. Достатній рівень
7.
![]() Знайти
первісну для функції f (x) = x ,
графік якої проходить через точку М(4;2).
Знайти
первісну для функції f (x) = x ,
графік якої проходить через точку М(4;2).
8. Знайти площу фігури, обмеженої лініями: y = 2x ; y = 3−x .
9. Знайти об’єм тіла обертання, утвореного обертанням навколо осі Ох фігури, обмеженої лініями: y=2x−x2 ; y = 0 ; x =1; x = 2.
Завдання: IV. Високий рівень
|
10. Знайти первісну для функції
11. Знайти площу фігури, обмеженої лініями: 12. Знайти об’єм тіла, утвореного обертанням навколо осі |
|
, графік якої проходить через
Ох фігури, обмеженої |
|||||
|
|
|||||||
|
лініями: |
y=2x2 −1 |
; |
y=−x2 +3x |
. |
|||
|
|||||||
ІІІ. Актуалізація опорних знань.
Метод «АДВОКАТИ»
Кожен учень задає своєму сусідові по парті по одному запитанню. Вчитель бачить, хто зрозумів, а хто – ні.
• Що називаємо первісною для функції f(x)?
• Чи правда що F(x) = x2 є первісною для функції f(x) = 2x.
• Яка теорема показує, як пов’язані між собою всі первісні даної функції?
• Який запис називають загальним виглядом первісної?
• Що ми називаємо невизначеним інтегралом?
• Яка первісна функції ех (F(x) = )
• Чи є функція F(x) = 3x2+x- 2 первісною для f(x)=6х+1?
• Чи є функція F(x) = 5 – 3 первісною для функції f(x) = – ?
• Які властивості має площа фігури?
• Первісною для якої величини є: а) закон руху; б) швидкість руху?
b
• Який фізичний зміст має формула: ∫ f ′(x)d =x f (b)− f (a)?
a
IV УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ЗНАНЬ, УМІНЬ І НАВИЧОК
УРОК ПРОВОДИТЬСЯ ЗА ТИПОМ ГРИ « КВК»
Змагаються дві команди: « Первісна» і « Інтеграл»
Кожний конкурс оцінюється в один бал за правильність виконання і один бал за швидкість розв’язування. Результати гри будуть заноситися в перевірочний лист.
КОНКУРС « РОЗМИНКА» - 5 хвилини.
Це самостійна робота учнів. Виграє та команда, в якій більша кількість учнів правильно розв’язала і вчасно здала завдання.
|
№з\п |
ЗАВДАННЯ |
БАЛИ |
||||
|
1 |
|
|
б) |
|
в) |
3 |
|
|
|
|||||
|
2 |
|
1 |
||||
КОНКУРС «БЛІЦТУРНІР» Перший раунд «ВІДШУКАЙ МЕНЕ!» - 5 хвилини.
Потрібно для кожної функції відшукати відповідну первісну та поставити в правій частині таблиці відповідну літеру, щоб утворились закодовані слова.
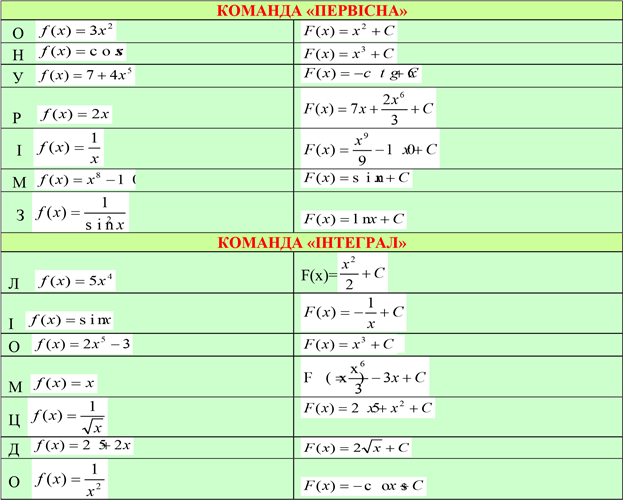
Другий раунд «УГОРСЬКИЙ КРОСВОРД» час виконання –5 хвилини Кожна команда розгадує кросворд на місцях, а потім перевіряємо.
|
Р |
А |
Н |
Т |
Е |
Я |
І |
|
Х |
І |
І |
Р |
Г |
О |
Р |
|
Е |
М |
В |
У |
Т |
Е |
Д |
|
Д |
Н |
А |
Р |
Е |
Ф |
И |
|
І |
Н |
Я |
Е |
Н |
Н |
Я |
|
Н |
Т |
Ц |
Н |
А |
Е |
Л |
|
Н |
Т |
Ц |
Н |
А |
Е |
Л |
|
Р |
А |
Л |
А |
Ц |
І |
Н |
Питання до кросворду:
1. Ключ до практики…
2. Операція знаходження первісної функції називається…
3. Яке поняття виникло з практичної потреби людей знаходити площі неплоских фігур…
4. Хто вніс у вивчення інтегрального числення найбільший внесок?..
5. Інтегрування – операція, обернена до…
b
6.
![]() ∫
f (x)d =x F(x)ba − формула
Ньютона…
∫
f (x)d =x F(x)ba − формула
Ньютона…
a
КОНКУРС « МАТЕМАТИЧНИЙ ФУТБОЛ»
Кожній команді пропонується малюнок, за яким вона придумує питання і «відфутболює» конкретному учаснику іншої команди. Виграє та команда, яка дасть більше правильних відповідей( час виконання – 5 хвилин, 1 хвилина на складання запитання).
Команда «Первісна» Команда «Інтеграл»
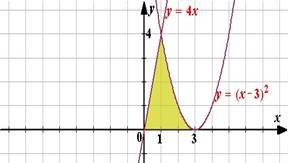
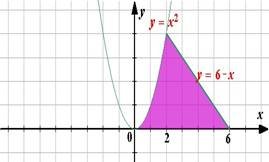
КОНКУРС КАПІТАНІВ
Капітани одержують картки із завданнями. Поки вони готуються біля дошки, команди виконують ті ж самі завдання на окремих аркушах. Виконавши завдання, капітани пояснюють його і ставлять питання один одному. Переможцем визначається капітан, який першим правильно виконав завдання( час виконання – 5 хвилин)
ЗАВДАННЯ ДЛЯ КАПІТАНІВ:
|
КОМАНДА «ПЕРВІСНА» |
||||||
|
1.Обчислити площу фігури, обмеженої параболою |
y=6−x2 |
і прямою |
y = 2 |
|
||
|
|
||||||
|
КОМАНДА « ІНТЕГРАЛ» |
||||||
|
1.Обчислити площу фігури, обмеженої параболою |
y =1−x2 |
і віссю |
Ox |
|
||
|
|
||||||
КОНКУРС «ПОМІРКУЙ»
Кожній команді пропонуються вправи, перемагає та команда, учасники якої за певний час (8 хвилин) найбільше і правильно виконають задач. Одна правильна відповідь – 1бал.
|
|
ОБЧИСЛИТИ ІНТЕГРАЛИ: |
|
||||||||||||||||
|
1. |
2 ∫(3x2 − 2x)d 1 |
x |
2. |
|
|
3. |
|
|
|
|
||||||||
|
|
||||||||||||||||||
|
|
||||||||||||||||||
|
5. |
0 |
|
6. |
dx
|
|
7. |
π
|
|
|
|
||||||||
|
|
||||||||||||||||||
|
|
||||||||||||||||||
|
9. |
|
x |
|
π
|
|
|
π |
|
|
12. |
||||||||
|
|
|
x |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
14. |
π cos2 x |
|
|
3 (2x2 − 5)d x |
|
|
|||||||||
|
|
∫ 0 |
x |
||||||||||||||||
|
|
|
|||||||||||||||||
|
|
||||||||||||||||||
|
||||||||||||||||||
V ПІДБИТТЯ ПІДСУМКІВ
Кожному учаснику з команди пропонується оцінити свого товариша за допомогою листа взаємоперевірки. Журі оголошує результати гри.
VI Рефлексія
Учням пропоную висловитися з питання:
1.Які пізнавальні процеси були задіяні на уроці найбільше (мислення, пам’ять, увага, уява)?
2. Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі).
3. Чи отримали ви задоволення від власної праці?
4. Охарактеризуйте свій емоційний стан протягом уроку (хвилювались, дивувались, зосереджувались) та в кінці уроку (задоволені, виснажені, впевнені, раді, успішні).
5.Чи є бажання повторити свої відчуття?
VII Домашнє завдання
1. Скласти кросворд за темою «Інтеграл і його застосування»
2. Підготуватися до тематичної атестації.
ДОДАТКИ:
Аркуш для перевірки
|
ВИДИ КОНКУРСІВ |
НАЗВА КОМАНДИ |
|
|
«ПЕРВІСНА» |
«ІНТЕГРАЛ» |
|
|
1.Розминка |
|
|
|
2.Бліцтурнір: |
|
|
|
а)»Відшукай мене» |
|
|
|
б)угорський кросворд |
|
|
|
3.Математичний футбол |
|
|
|
4.Конкурс капітанів |
|
|
|
5.Поміркуй |
|
|
|
ПІДСУМОК |
|
|

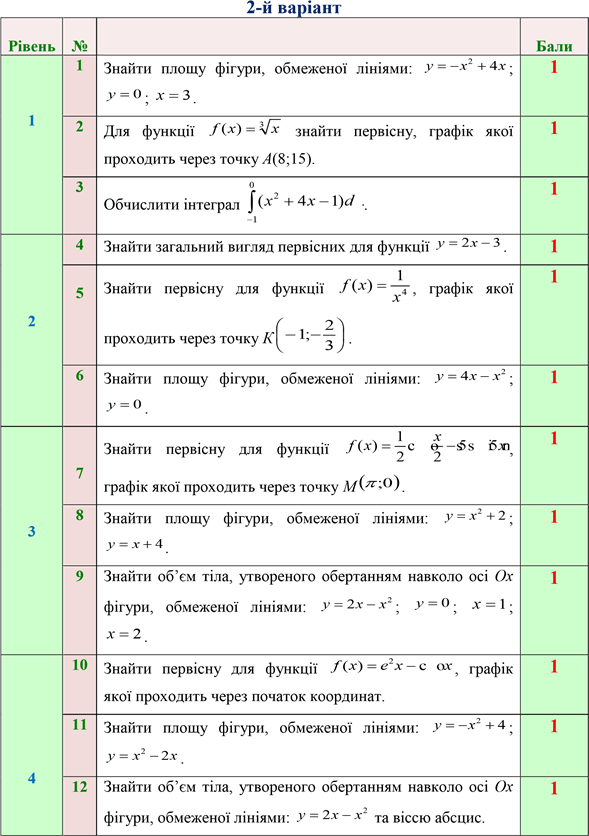 Завдання
Завдання
Домашнє завдання.
1.Повторити вивчений матеріал 2 Виконати завдання сусіднього варіанту.
Додаток 1 Інструкція по роботі в малих групах
(дає змогу набути навичок спілкування та співпраці)
Після об’єднання вас у малі групи ви повинні за короткий час (3-5 хв.) виконати завдання та представити результати роботи своєї групи Правила роботи в малих групах
1. Швидко розподіліть ролі в групі. Визначтесь хто буде головуючим, посередником, секретарем, доповідачем. Намагайтесь виконувати різні ролі.
Головуючий (спікер):
• зачитує завдання групи:
♦ організовує порядок виконання;
♦ пропонує учасникам групи висловитись по черзі;
♦ заохочує групу до роботи;
♦ підбиває підсумки роботи;
♦ за згодою групи визначає доповідача.
Секретар:
♦ веде коротко і розбірливо записи результатів роботи своєї групи;
♦ як член групи має бути готовим висловити думку групи при підбитті підсумків або допомогти доповідачеві.
Посередник:
♦ стежить за часом; ♦ заохочує групу до роботи.
Доповідач:
♦ чітко висловлю думку, до якої дійшла група; ♦ доповідає про результати роботи групи.
2. Починайте висловлюватися спочатку за бажанням, а потім по черзі.
3. Дотримуєтесь правил активного слухання, головне не перебивайте один одного.
4. Обговорюєте ідеї, а не особи учнів, які висловили цю ідею.
5. Утримуйтесь від оцінок та образ учасників групи.
6. Намагайтеся дійти спільної думки, хоча в деяких випадках у групі може бути с особлива думка і вона має право на існування.
Додаток 2 Картка – інструкція правил роботи учня у інтерактивній технології
«Ажурна пилка»
|
Порядок дій |
1 |
Спочатку ви працюватимете в «домашній» групі |
|
2 |
В іншій групі ви будете в ролі «експертів» з питань, над якими ви працювали в «домашній» групі, та отримаєте інформацію від представників інших груп |
|
|
3 |
В останній частині заняття повертайтесь в свою «домашню» групу, для того, щоб поділитись новою інформацією, яку вам надали учасники інших груп |
|
|
Ви в «домашній» групі |
1 |
Кожна група отримує завдання, вивчає його та обговорює с вій матеріал |
|
2 |
Вибирає головуючого, тайм - скіпера, оперативника |
|
|
Ви в «експертній» групі |
1 |
Після об’єднання у нові групи ви стаєте експертами з тієї теми, що вивчалася в вашій «домашній» групі |
|
2 |
По черзі ви якісно і в повному обсязі доводите інформацію до членів інших груп та сприймаєте нову інформацію від |
|
|
Ви в «домашній»групі |
1 |
Ви повертаєтесь до «дому», де маєте поділитися інформацією з членами своєї «домашньої» групи |
|
2 |
Виробляєте спільні висновки та рішенн |
Додаток 3
Картка – інструкція правил роботи учня
у інтерактивній технології «Мікрофон»
для обговорення та засвоєння теоретичного матеріалу
Для того, щоб створити атмосферу довіри та взаємоповаги необхідно прийняти правила спілкування:
1. Говорити по черзі;
2. Чітко висловлювати свою думку;
3. Не перебивати того, хто говорить;
4. Критикувати ідеї, а не особу, що їх висловила; 5. Бути позитивними;
6. Говорити від себе.
[1] 7; 2) 1x ; 3) x13 ; 4) 5![]() x ; 5)
x ; 5) ![]() 31x ; 6) ex;
31x ; 6) ex;
1) х x;
8) ![]() cos12 x ; 9) sin12 x ; 10) cos х;
11) sin х; 12) x x
cos12 x ; 9) sin12 x ; 10) cos х;
11) sin х; 12) x x
7) π


про публікацію авторської розробки
Додати розробку


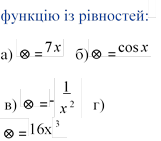
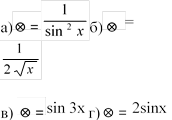
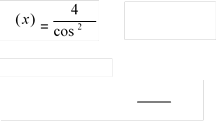
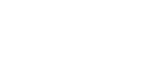
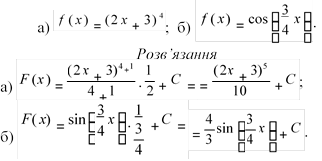
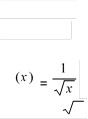
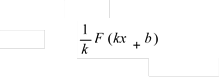
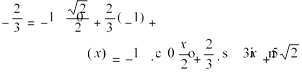

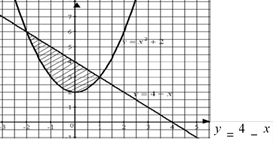

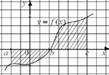
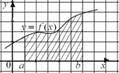

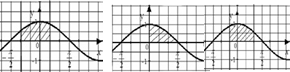
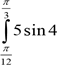 xdx
xdx 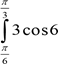 xdx
xdx