Розв'язки "Завдання ЗНО з математики ІІІ частина"
Міністерство освіти і науки України
НВК: загальноосвітня школа І-ІІ ступенів №34 –
економіко-правовий ліцей «Сучасник» - ДЮЦ
Розв’язки завдань
частини №3
зовнішнього тестування
Вчитель математики,
інформатики та економіки
НВК Костюкевич П.П.
Кіровоград - 2019
Варіант 1 (2006 рік)
37. Дано правильний шестикутник ![]() зі стороною 2см. Знайдіть:
зі стороною 2см. Знайдіть:
а) площу шестикутника;
б) значення параметра ![]() , при якому вектори
, при якому вектори ![]() і
і ![]() перпендикулярні;
перпендикулярні;
в) довжину вектора ![]() , де точки
, де точки ![]() - середини сторін
- середини сторін ![]() відповідно.
відповідно.
Розв’язання:
 а)
а) ![]() , де
, де ![]() - сторона шестикутника.
- сторона шестикутника. ![]() .
.
б) Введемо прямокутну декартову систему координат: центр – точка ![]() ; вісь абсцис співпадає з напрямком вектора
; вісь абсцис співпадає з напрямком вектора ![]() ; вісь ординат така, що вектор
; вісь ординат така, що вектор ![]() лежить в першій чверті. В цій системі координат маємо:
лежить в першій чверті. В цій системі координат маємо: ![]() , тоді
, тоді ![]() . Необхідно, щоб
. Необхідно, щоб ![]() (необхідна умова перпендикулярності векторів).
(необхідна умова перпендикулярності векторів).
![]() .
.
в) Запишемо координати точок ![]() та
та ![]() , тоді
, тоді  .
. ![]() .
.
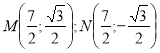 .
. ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
38. Задано функцію  . Знайдіть:
. Знайдіть:
а) область визначення функції;
б) нулі заданої функції;
в) усі розв’язки нерівності ![]() .
.
Розв’язання:
а) Область визначення знаходимо, розв’язавши систему:  , де
, де ![]() . Графічно розв’язок системи зображено на малюнку 1.
. Графічно розв’язок системи зображено на малюнку 1.

![]() .
.
б) Маємо рівняння: ![]() . Останнє рівняння підносимо до квадрату:
. Останнє рівняння підносимо до квадрату: ![]()
![]()
![]() . Очевидно, що
. Очевидно, що ![]() , отже, це значення не потрапляє в ОДЗ.
, отже, це значення не потрапляє в ОДЗ.
в) Позначимо: ![]() . Нерівність
. Нерівність ![]() еквівалентна сукупності систем:
еквівалентна сукупності систем:  . Графічно розв’язки систем показано на малюнках 2. 3. Розв’язками будуть інтервали, на яких збігаються розв’язки нерівностей. (На графіку – накладання).
. Графічно розв’язки систем показано на малюнках 2. 3. Розв’язками будуть інтервали, на яких збігаються розв’язки нерівностей. (На графіку – накладання).
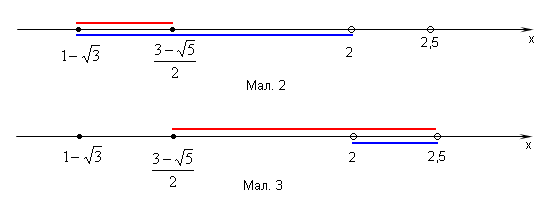
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) 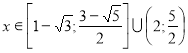 .
.
Варіант 2 (2006 рік)
 37. Основою чотирикутної піраміди
37. Основою чотирикутної піраміди ![]() є квадрат
є квадрат ![]() . Ребро
. Ребро ![]() перпендикулярне до площини основи піраміди. Точка
перпендикулярне до площини основи піраміди. Точка ![]() - середина ребра
- середина ребра ![]() . Площина
. Площина ![]() утворює з площиною основи піраміди кут
утворює з площиною основи піраміди кут ![]() . Знайдіть площу трикутника
. Знайдіть площу трикутника ![]() , якщо довжина ребра
, якщо довжина ребра ![]() дорівнює
дорівнює ![]() .
.
Розв’язання:
Розглянемо піраміду ![]() , в якій
, в якій ![]() ,
, ![]() - середина
- середина ![]() . Площина
. Площина ![]() , оскільки містить перпендикуляр, проведений до основи. Проведемо
, оскільки містить перпендикуляр, проведений до основи. Проведемо ![]() , тоді
, тоді ![]() і
і ![]() . Проведемо
. Проведемо ![]() , тоді за теоремою про три перпендикуляри
, тоді за теоремою про три перпендикуляри ![]() і
і ![]() (лінійний кут двогранного кута). З
(лінійний кут двогранного кута). З ![]() :
: ![]() .
. ![]() - середня лінія
- середня лінія ![]() , тому
, тому ![]() . В основі піраміди лежить квадрат, тому
. В основі піраміди лежить квадрат, тому ![]() . Шукана площа:
. Шукана площа: ![]() .
.
Відповідь: ![]() .
.
38. Задано нерівність ![]() .
.
а) Знайдіть множину допустимих значень ![]() та
та ![]() .
.
б) Побудуйте у прямокутній декартовій системі координат множину точок ![]() , координати яких задовольняють задану нерівність.
, координати яких задовольняють задану нерівність.
в) Знайдіть площу фігури з пункту б).
Розв’язання:
а)  . Це множина точок площини, які лежіть поза кругом з центром в точці (0;0) і радіусом
. Це множина точок площини, які лежіть поза кругом з центром в точці (0;0) і радіусом ![]() .
.
 б) в)
б) в) ![]()
Відповідь: в) ![]()
Варіант 3 (2006 рік)

37. Основа висоти трикутної піраміди ![]() , проведеної із вершини
, проведеної із вершини ![]() , збігається з точкою перетину висот трикутника
, збігається з точкою перетину висот трикутника ![]() . Відомо, що
. Відомо, що ![]() .
.
- Доведіть, що бічні грані піраміди є прямокутними трикутниками.
-
Знайдіть відношення площ граней
 і
і 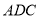 .
.
Розв’язання:
a) Нехай ![]() - висота піраміди,
- висота піраміди, ![]() - ортоцентр
- ортоцентр ![]() .
. ![]() , але
, але ![]() - проекція
- проекція ![]() на
на ![]() . За теоремою про три перпендикуляри
. За теоремою про три перпендикуляри ![]() . Аналогічно,
. Аналогічно, ![]() .
.
В площині ![]() через точку
через точку ![]() проведемо
проведемо ![]() , тоді
, тоді ![]() . Пряма
. Пряма ![]() (
(![]() - прямокутний, оскільки
- прямокутний, оскільки ![]() ). За ознакою перпендикулярності прямої і площини
). За ознакою перпендикулярності прямої і площини ![]() . Аналогічно доводиться
. Аналогічно доводиться ![]() . Для цього в площині
. Для цього в площині ![]() треба провести через точку
треба провести через точку ![]() пряму паралельно до
пряму паралельно до ![]() .
.
b) ![]()
Відповідь: b) 0,75
38. Задано рівняння ![]() .
.
-
Розв’яжіть рівняння при
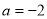 .
.
-
Знайдіть усі значення параметра
 , при яких дане рівняння не має коренів.
, при яких дане рівняння не має коренів.
Розв’язання:
a) При ![]() рівняння має вигляд
рівняння має вигляд ![]() . Розділимо на
. Розділимо на ![]() . Маємо:
. Маємо:  . Нехай
. Нехай  , тоді рівняння набуває вигляду:
, тоді рівняння набуває вигляду:
![]() . Отже, дане рівняння розв’язків немає.
. Отже, дане рівняння розв’язків немає.
b) Розглянемо квадратне рівняння ![]() . Якщо це рівняння не буде мати коренів або вони будуть недодатними, то дане рівняння не буде мати коренів.
. Якщо це рівняння не буде мати коренів або вони будуть недодатними, то дане рівняння не буде мати коренів.
В першому випадку необхідно і достатньо, щоб ![]() .
.
Якщо ![]() , то один з коренів обов’язково додатній і дане рівняння корені має.
, то один з коренів обов’язково додатній і дане рівняння корені має.
Якщо ![]() , то
, то ![]() . Отже,
. Отже, ![]() - розв’язок.
- розв’язок.
Якщо ![]() , то звернемось до геометричної інтерпретації.
, то звернемось до геометричної інтерпретації.
 Умову задачі задовольняє система
Умову задачі задовольняє система  . Обидві нерівності виконуються при
. Обидві нерівності виконуються при ![]() .
.
Відповідь: ![]() .
.
Варіант 4 (2006 рік)
37. Трикутник ![]() , сторона
, сторона ![]() якого дорівнює 4см і кут
якого дорівнює 4см і кут ![]() дорівнює
дорівнює ![]() , вписано в коло радіуса
, вписано в коло радіуса ![]() см. Знайдіть:
см. Знайдіть:
-
 Довжину сторони
Довжину сторони  ;
;
-
Довжину середньої лінії трикутника, яка паралельна
 ;
;
-
Відстань між точками кола, у яких пряма, що містить середню лінію трикутника
 , паралельну до сторони
, паралельну до сторони  , перетинає коло.
, перетинає коло.
Розв’язання:
a) З ![]() (теорема синусів):
(теорема синусів): ![]() см
см
b) Нехай ![]() - середина
- середина ![]() ;
; ![]() - середина
- середина ![]() , тоді
, тоді ![]() . Знаходимо
. Знаходимо ![]() за теоремою косинусів з
за теоремою косинусів з ![]()
![]() ;
;
![]() ;
; ![]() , тоді
, тоді ![]() .
.
c) Нехай ![]() , де
, де ![]() - точки на колі, відстань між якими треба знайти. Скористаємось властивістю хорд, що перетинаються в колі.
- точки на колі, відстань між якими треба знайти. Скористаємось властивістю хорд, що перетинаються в колі.  . Віднімаємо від другого рівняння перше.
. Віднімаємо від другого рівняння перше. ![]() . З першого рівняння системи
. З першого рівняння системи ![]() ;
;![]() .
.
![]() .
.
Відповідь: а) 6см; b) ![]() см; с)
см; с) ![]() см.
см.
38. Задана нерівність ![]() .
.
-
Обчисліть площу фігури, яка визначається розв’язками нерівності при
 .
.
-
Знайдіть значення
 , при яких геометрична фігура має лише одну спільну точку з віссю ординат.
, при яких геометрична фігура має лише одну спільну точку з віссю ординат.
-
Визначте максимальне значення параметра
 , при якому вісь абсцис ділить задану фігуру на дві частини, площі яких відносяться як 1 : 7.
, при якому вісь абсцис ділить задану фігуру на дві частини, площі яких відносяться як 1 : 7.
Розв’язання:
 а)
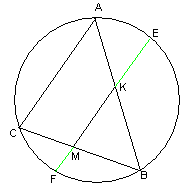
а)  При
При ![]() маємо квадрат, який зображено на мал.1. Його площа
маємо квадрат, який зображено на мал.1. Його площа ![]() .
.

Мал. 1 Мал. 2 Мал. 3
b) На малюнку 2 зображено два можливих положення квадратів, при якому вони мають лише одну спільну точку з віссю ординат. Цим положенням відповідають значення ![]() .
.
с) Якщо положення квадрата при ![]() прийняти за початкове і почати збільшувати
прийняти за початкове і почати збільшувати ![]() , то квадрат починає рухатись вліво і вгору, не змінюючи своїх розмірів. Вісь абсцис розбиває квадрат на дві фігури, причому кожному значенню
, то квадрат починає рухатись вліво і вгору, не змінюючи своїх розмірів. Вісь абсцис розбиває квадрат на дві фігури, причому кожному значенню ![]() відповідає єдине відношення площ цих фігур. Для того, щоб це відношення дорівнювало 1 : 7, необхідно, щоб
відповідає єдине відношення площ цих фігур. Для того, щоб це відношення дорівнювало 1 : 7, необхідно, щоб ![]() . Це можливо за умови
. Це можливо за умови ![]() , тоді
, тоді ![]() і
і ![]() .
.
Відповідь: а) 2; b) ![]() ; с)
; с) ![]() .
.
 Варіант 5 (2006 рік)
Варіант 5 (2006 рік)
37. У прямокутну трапецію ![]() вписано коло. Бічна сторона
вписано коло. Бічна сторона ![]() ділиться точкою дотику на відрізки 4 см і 9 см. Знайдіть:
ділиться точкою дотику на відрізки 4 см і 9 см. Знайдіть:
а) висоту трапеції;
б) відношення довжин відрізків, на які центр кола ділить середню лінію трапеції;
в) кут, під яким видно сторону ![]() із центра кола.
із центра кола.
Розв’язання:
а) Позначимо точки дотиків кола до сторін трапеції ![]() через
через ![]() відповідно.
відповідно. ![]() (як відрізки дотичних, проведених до кола з однієї точки). Розглянемо
(як відрізки дотичних, проведених до кола з однієї точки). Розглянемо ![]() . Для нього
. Для нього ![]() , тоді
, тоді ![]() .
.
б) ![]() (радіус вписаного кола), тоді
(радіус вписаного кола), тоді ![]() ;
; ![]() ;
; ![]() . Отже,
. Отже, ![]() .
.
в) З ![]()
![]() ;
;
з ![]()
![]() . Тоді для трикутника
. Тоді для трикутника ![]() маємо:
маємо: ![]() , тобто для цього трикутника виконується теорема Піфагора
, тобто для цього трикутника виконується теорема Піфагора ![]() .
.
Відповідь: а) 12 см; б) 12:13; в) ![]() .
.
38. Задано функції: ![]() і
і ![]() . Знайдіть:
. Знайдіть:
а) найбільше і найменше значення функції ![]() ;
;
б) найбільше і найменше значення функції ![]() ;
;
в) корені рівняння найбільше і найменше значення функції ![]() .
.
Розв’язання:
а) Оскільки ![]() , то
, то ![]() .
.
 б) Знаходимо ОДЗ:
б) Знаходимо ОДЗ: ![]() . Далі,
. Далі, ![]() .
.
![]() , отже
, отже ![]() .
.
в) Оскільки ![]() , то рівняння
, то рівняння ![]() еквівалентне системі
еквівалентне системі  .
.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Варіант 6 (2006 рік)
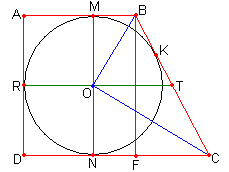
37. У трикутній піраміді ![]() три бічні ребра
три бічні ребра ![]() і
і ![]() - діляться точками
- діляться точками ![]() у відношеннях 1 : 4, 1 : 3, 2 : 3, починаючи від вершини
у відношеннях 1 : 4, 1 : 3, 2 : 3, починаючи від вершини ![]() , відповідно. Знайдіть:
, відповідно. Знайдіть:
-
Відношення площ трикутників
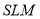 і
і  .
.
-
Відношення об’ємів пірамід
 і
і  .
.
Розв’язання:
a) Нехай ![]() .
. ![]()
![]()
![]() .
.
Отже, ![]() .
.
b) Побудуємо площину ![]() . В цій площині проведемо
. В цій площині проведемо ![]() та
та ![]() . Крім того,
. Крім того, ![]() Трикутник
Трикутник![]() подібний до трикутника
подібний до трикутника ![]() , причому
, причому ![]() .
.
![]()
Відповідь: a) ![]() ; b)
; b) ![]() .
.
38. Задано функцію ![]() , де
, де ![]() . Знайдіть:
. Знайдіть:
-
 Рівняння дотичної, проведеної до графіка функції у точці з абсцисою
Рівняння дотичної, проведеної до графіка функції у точці з абсцисою 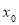 .
.
-
Площу трапеції, утвореної дотичною з пункту а) і прямими
 .
.
-
У якій точці графіка функції
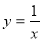 треба провести дотичну, щоб площа трапеції з пункту b) була найбільшою.
треба провести дотичну, щоб площа трапеції з пункту b) була найбільшою.
Розв’язання:
a) Загальне рівняння дотичної: ![]() .
.
![]() ;
; ![]() .
.
![]() (1)
(1)
b) Довжини основ трапеції – це значення функції (1) в точках ![]() та
та ![]() відповідно.
відповідно.
Висота трапеції дорівнює 1. Отже, ![]() (2).
(2).
с) Досліджуємо функцію ![]() на максимум.
на максимум. ![]() точка максимуму.
точка максимуму.
Відповідь: a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()

Варіант 7 (2006 рік)
37. В основі піраміди лежить рівносторонній трикутник зі стороною ![]() . Одна з бічних граней перпендикулярна до площини основи і також є рівностороннім трикутником. Навколо піраміди описана куля. Знайдіть:
. Одна з бічних граней перпендикулярна до площини основи і також є рівностороннім трикутником. Навколо піраміди описана куля. Знайдіть:
- Довжину висоти піраміди, обґрунтувавши її положення.
- Радіус кулі, описаної навколо піраміди.
Розв’язання:
-
Бічна грань
 , тому містить висоту піраміди. Оскільки
, тому містить висоту піраміди. Оскільки 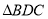 - правильний, то його висота
- правильний, то його висота  і є висотою піраміди.
і є висотою піраміди. 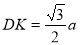 .
.
-
Нехай
 - центр описаної кулі, тому точка
- центр описаної кулі, тому точка  рівновіддалена від
рівновіддалена від 
 проекція точки
проекція точки  на
на 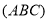 точка
точка  - центр кола, описаного навколо
- центр кола, описаного навколо  . Крім того, точка
. Крім того, точка 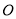 рівновіддалена від точок
рівновіддалена від точок  , тому
, тому  . З
. З  маємо:
маємо: 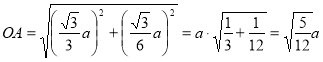
Відповідь: a) ![]() ; b)
; b) ![]() .
.
38. Задано тригонометричне рівняння ![]() . Укажіть:
. Укажіть:
-
При яких значеннях параметра
 рівняння має розв’язки.
рівняння має розв’язки.
-
Найменший додатний розв’язок рівняння для найбільшого значення параметра
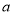 , при якому рівняння має розв’язки.
, при якому рівняння має розв’язки.
Розв’язання:
-
Запишемо рівняння у вигляді
 або
або
 , отже, для існування розв’язків необхідно
, отже, для існування розв’язків необхідно ![]() .
.
-
При
 маємо рівняння
маємо рівняння  . Найменший додатний розв’язок отримаємо при
. Найменший додатний розв’язок отримаємо при 
 .
.
Відповідь: a) ![]() ; b)
; b) ![]() .
.
Варіант 8 (2006 рік)
 37. Бічне ребро правильної чотирикутної піраміди нахилене до площини основи під кутом
37. Бічне ребро правильної чотирикутної піраміди нахилене до площини основи під кутом ![]() . У піраміду вписано куб так, що одна його грань лежить у площині основи піраміди, а чотири вершини протилежної грані – на бічних ребрах піраміди. Знайдіть:
. У піраміду вписано куб так, що одна його грань лежить у площині основи піраміди, а чотири вершини протилежної грані – на бічних ребрах піраміди. Знайдіть:
а) відношення об’ємів піраміди та куба;
б) значення ![]() , при якому відношення об’ємів піраміди і куба буде найменшим.
, при якому відношення об’ємів піраміди і куба буде найменшим.
Розв’язання:
a) Нехай ![]() - сторона основи правильної чотирикутної піраміди
- сторона основи правильної чотирикутної піраміди ![]() , тоді
, тоді ![]() (
( ![]() - точка перетину діагоналей основи). З
- точка перетину діагоналей основи). З ![]() :
: ![]() . Об'єм піраміди:
. Об'єм піраміди: ![]() .
.
Нехай ![]() - ребро куба. З
- ребро куба. З ![]() :
: ![]() , тоді
, тоді ![]() або
або ![]() . Таким чином,
. Таким чином, ![]()
 . Об'єм куба:
. Об'єм куба: 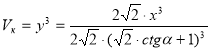 . Шукане відношення:
. Шукане відношення: 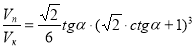 .
.
б) Нехай ![]() . Розглянемо функцію
. Розглянемо функцію ![]() . Досліджуємо її на мінімум.
. Досліджуємо її на мінімум. ![]() .
. ![]() - точка мінімуму, отже
- точка мінімуму, отже ![]() .
.
Відповідь: а) ![]() ; б)
; б) ![]() .
.
38. Розв’яжіть нерівність: ![]() .
.
Розв’язання:
Знаходимо ОДЗ:  . Якщо
. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() . Отже, ОДЗ
. Отже, ОДЗ ![]() .
.
Запишемо нерівність у вигляді: ![]() . Нехай
. Нехай ![]() .
. ![]() .
.
При ![]() нерівність очевидно виконується. Для
нерівність очевидно виконується. Для ![]() піднесемо нерівність до квадрату.
піднесемо нерівність до квадрату. ![]() . Розв’язок нерівності відносно
. Розв’язок нерівності відносно ![]() :
: ![]() . Повертаємось до змінної
. Повертаємось до змінної ![]() :
: ![]() або
або ![]() . Остання нерівність еквівалентна системі:
. Остання нерівність еквівалентна системі:  , де
, де ![]() . Отже,
. Отже,  . Отримана множина є підмножиною ОДЗ.
. Отримана множина є підмножиною ОДЗ.
Відповідь: ![]() .
.
Варіант 9 (2006 рік)
37. У правильній трикутній піраміді ![]() кут між бічним ребром і площиною основи дорівнює
кут між бічним ребром і площиною основи дорівнює ![]() . Сторона основи дорівнює
. Сторона основи дорівнює ![]() .
. ![]() - висота піраміди.
- висота піраміди.
-
Побудуйте переріз піраміди, який проходить через точку
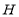 паралельно ребрам
паралельно ребрам 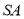 і
і  .
.
- З’ясуйте, якою геометричною фігурою є цей переріз (відповідь обґрунтуйте).
- Знайдіть площу перерізу.
 Розв’язання:
Розв’язання:
a) Оскільки піраміда правильна, то точка ![]() - це точка перетину медіан трикутника
- це точка перетину медіан трикутника ![]() . Проведемо медіану
. Проведемо медіану ![]() (
(![]() - середина
- середина ![]() ).
). ![]() . В площині
. В площині ![]() проведемо
проведемо ![]() ,
, ![]() . Через точку
. Через точку ![]() в площині
в площині ![]() проводимо
проводимо ![]() . В площині
. В площині ![]() проводимо
проводимо ![]() . В площині
. В площині ![]() проводимо
проводимо ![]() . З’єднуємо
. З’єднуємо ![]() та
та ![]() . Переріз
. Переріз ![]() - шуканий.
- шуканий.
b) Трикутники ![]() та
та ![]() подібні за двома кутами (
подібні за двома кутами (![]() - спільний,
- спільний, ![]() як відповідні) і оскільки
як відповідні) і оскільки ![]() - точка перетину медіан, то
- точка перетину медіан, то ![]() . З подібності пар трикутників
. З подібності пар трикутників ![]() та
та ![]() , враховуючи коефіцієнт подібності та паралельність, маємо:
, враховуючи коефіцієнт подібності та паралельність, маємо: ![]() - паралелограм Далі,
- паралелограм Далі, ![]() . Відрізок
. Відрізок ![]() містить проекцію похилої
містить проекцію похилої ![]() , тому за теоремою про три перпендикуляри
, тому за теоремою про три перпендикуляри ![]() .
. ![]() . Таким чином, паралелограм
. Таким чином, паралелограм ![]() є прямокутником.
є прямокутником.
с) ![]() ;
; ![]() .
. ![]()
Відповідь: переріз є прямокутником, площа якого ![]() .
.
38. Знайдіть усі цілі значення параметра ![]() , при яких рівняння
, при яких рівняння ![]() має дійсні корені. Знайдіть ці корені.
має дійсні корені. Знайдіть ці корені.
Розв’язання:
![]()

 .
.
Відповідь: якщо ![]() , то
, то ![]() .
.
Варіант 10 (2006 рік)
37. Переріз площиною правильної чотирикутної піраміди, у якої бічне ребро дорівнює стороні основи, зроблено так, що отриманий многокутник має максимальну кількість сторін, а всі його вершини, крім однієї, є серединами ребер піраміди. Знайдіть:
- Кількість сторін многокутника, що є перерізом піраміди.
- Косинус кута нахилу площини перерізу до основи піраміди.
-
 Відношення площі перерізу до площі основи піраміди.
Відношення площі перерізу до площі основи піраміди.
Розв’язання:
а) Розглянемо правильну чотирикутну піраміду ![]() ,
, ![]() - основа,
- основа, ![]() - висота. Проводимо
- висота. Проводимо ![]() - середню лінію
- середню лінію ![]() та
та ![]() - середню лінію
- середню лінію ![]() . Нехай
. Нехай ![]() . Проводимо
. Проводимо ![]() до перетину з
до перетину з ![]() .
. ![]() - переріз піраміди, який має п’ять сторін.
- переріз піраміди, який має п’ять сторін.
b) Нехай ![]() - косинус якого треба знайти.
- косинус якого треба знайти. ![]() .
.
З трикутника ![]() :
: ![]() , тоді
, тоді ![]() . З трикутника
. З трикутника ![]() :
: ![]() . Отже,
. Отже, ![]() .
.
с) Нехай ![]() , тоді
, тоді ![]() - рівнобедрений.
- рівнобедрений. ![]() , тоді
, тоді ![]() .
.
Знаходимо площу п’ятикутника ![]() , який є ортогональною проекцією перерізу.
, який є ортогональною проекцією перерізу.
![]() , тоді
, тоді ![]()
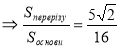
Відповідь: а) 5; b) ![]() ; с)
; с)  .
.
38. Задано функцію ![]() . Знайдіть:
. Знайдіть:
- Область визначення функції.
- Нулі функції.
-
Усі розв’язки нерівності
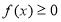 .
.
Розв’язання:
а) 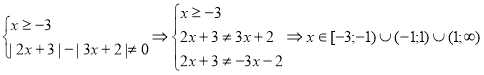
b) ![]() . Піднесемо до квадрату.
. Піднесемо до квадрату. ![]() ;
; ![]() . Перше значення не потрапляє в ОДЗ, друге – сторонній корінь рівняння, що розглядається.
. Перше значення не потрапляє в ОДЗ, друге – сторонній корінь рівняння, що розглядається.
![]() . Перше значення не потрапляє в ОДЗ.
. Перше значення не потрапляє в ОДЗ.
с) Розглянемо нерівності: ![]() ;
; ![]() ;
; ![]() . Для того, щоб мала місце нерівність
. Для того, щоб мала місце нерівність ![]() необхідно, щоб одночасно виконувались всі три нерівності або щоб виконувалась лише одна. Скористаємось геометричною інтерпретацією . На малюнку виділено розв’язки кожної з нерівностей.
необхідно, щоб одночасно виконувались всі три нерівності або щоб виконувалась лише одна. Скористаємось геометричною інтерпретацією . На малюнку виділено розв’язки кожної з нерівностей.
 Перший випадок (тобто, коли одночасно виконуються всі нерівності) не має місце при всіх
Перший випадок (тобто, коли одночасно виконуються всі нерівності) не має місце при всіх ![]() .
.
Залишається записати об’єднання проміжків, на яких виконується лише одна нерівність.
Відповідь: а) ![]() ; b)
; b) ![]() ; с)
; с) ![]() .
.
Варіант 11 (2006 рік)
37. Об'єм правильної трикутної призми дорівнює ![]() . Кут між діагоналями двох бічних граней, що проведені із однієї вершини, дорівнює
. Кут між діагоналями двох бічних граней, що проведені із однієї вершини, дорівнює ![]() . Знайти сторону основи призми.
. Знайти сторону основи призми.
 Розв’язання:
Розв’язання:
Нехай ![]() - сторона основи правильної трикутної призми
- сторона основи правильної трикутної призми ![]() . Проводимо діагоналі
. Проводимо діагоналі ![]() бічних граней.
бічних граней. ![]() .
. ![]() - рівнобедрений, оскільки призма правильна, то її бічні грані рівні прямокутники, у яких рівні діагоналі. Проведемо медіану
- рівнобедрений, оскільки призма правильна, то її бічні грані рівні прямокутники, у яких рівні діагоналі. Проведемо медіану ![]() , яка є висотою і бісектрисою.
, яка є висотою і бісектрисою.
З 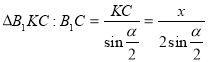 .
.
З 
 . Об'єм призми:
. Об'єм призми: ![]() .
. 
 .
.
Відповідь: 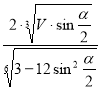 .
.
38. Задано рівняння ![]() .
.
-
Розв’яжіть рівняння при
 .
.
-
Розв’яжіть рівняння при всіх значеннях параметра
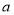 .
.
Розв’язання:
-
При
 маємо
маємо  .
.
-
При
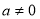 за умови
за умови 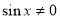 переходимо до еквівалентного рівняння:
переходимо до еквівалентного рівняння: 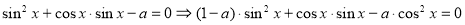 (1).
(1).
Якщо ![]() , то
, то  .
.
Якщо ![]() , то розділимо рівняння (1) на
, то розділимо рівняння (1) на ![]() . Отримаємо:
. Отримаємо:
![]() . Це квадратне рівняння відносно
. Це квадратне рівняння відносно ![]() .
. ![]() . Для існування розв’язків квадратного рівняння необхідно, щоб
. Для існування розв’язків квадратного рівняння необхідно, щоб ![]() . Тоді
. Тоді  .
.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то  ;
;  .
.
Варіант 12 (2006 рік)
37. Знайти перетин ![]() множин
множин ![]() ;
; ![]() .
.
Розв’язання:
Для множини А: ![]() ;
; ![]()
![]() . Якщо
. Якщо ![]() , то
, то ![]() . Отже, розв’язків немає.
. Отже, розв’язків немає. ![]() (*).
(*).
Для множини В: необхідно, щоб ![]() . За цієї умови
. За цієї умови ![]() (**).
(**).
Залишається з множини (*) вибрати ті значення, що потрапляють в (**).
![]() ;
;
![]() , бо
, бо ![]() .
.
![]() .
.
Відповідь: ![]() .
.
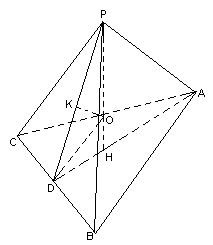 38. В правильній трикутній піраміді двогранний кут при основі дорівнює
38. В правильній трикутній піраміді двогранний кут при основі дорівнює ![]() . Знайти повну поверхню вписаного конуса, якщо радіус вписаної в піраміду кулі дорівнює
. Знайти повну поверхню вписаного конуса, якщо радіус вписаної в піраміду кулі дорівнює ![]() .
.
Розв’язання:
Розглянемо правильну трикутну піраміду ![]() . Множина точок, рівновіддалених від бічних граней – це висота піраміди
. Множина точок, рівновіддалених від бічних граней – це висота піраміди ![]() , тому центр вписаної кулі (точка О) лежить на висоті. Проведемо апофему бічної грані
, тому центр вписаної кулі (точка О) лежить на висоті. Проведемо апофему бічної грані ![]() .
. ![]() проекція
проекція ![]() на площину основи, отже
на площину основи, отже ![]() (лінійний кут двогранного кута). Центр вписаної кулі рівновіддалений від всіх граней, тому точка О належить бісектрисі
(лінійний кут двогранного кута). Центр вписаної кулі рівновіддалений від всіх граней, тому точка О належить бісектрисі ![]() .
.
Відповідь: ![]()
Варіант 13 (ЗНО - 2006 рік)
37. Основою прямого паралелепіпеда є квадрат ![]() зі стороною 3см. Бічне ребро
зі стороною 3см. Бічне ребро ![]() дорівнює 4см. Знайдіть площу перерізу паралелепіпеда площиною, що проходить через вершину
дорівнює 4см. Знайдіть площу перерізу паралелепіпеда площиною, що проходить через вершину ![]() перпендикулярно до прямої
перпендикулярно до прямої ![]() .
.
Розв’язання:
 Проводимо
Проводимо ![]() . В грані
. В грані ![]() через точку
через точку ![]() проводимо
проводимо ![]() . Паралелограм
. Паралелограм![]() - шуканий переріз. Доведемо, що цей паралелограм є прямокутником.
- шуканий переріз. Доведемо, що цей паралелограм є прямокутником. ![]() ,
, ![]() проекція
проекція ![]() на площину
на площину ![]() . За теоремою про три перпендикуляри
. За теоремою про три перпендикуляри ![]() , отже
, отже ![]() - прямокутник.
- прямокутник.
Нехай ![]() . Якщо
. Якщо ![]() , то
, то ![]() . Отже,
. Отже, ![]() подібний до
подібний до ![]() за двома кутами.
за двома кутами.
З ![]() .
.
З  . З подібності трикутників:
. З подібності трикутників:
 .
. ![]() . Шукана площа:
. Шукана площа:
![]() .
.
Відповідь: ![]() .
.
38. Розв’яжіть рівняння ![]() , якщо
, якщо ![]() .
.
Розв’язання:
![]() . Покладемо
. Покладемо ![]() , отримаємо рівняння
, отримаємо рівняння ![]() ;
; ![]() ;
; ![]() . Повертаємось до змінної
. Повертаємось до змінної ![]() .
.
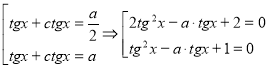 .
.
Для першого рівняння сукупності ![]() ; для другого
; для другого ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то
, то ![]() ;
; ![]() .
.
Варіант 14 (2007 рік)
36. Основою піраміди ![]() є квадрат
є квадрат ![]() . Грань
. Грань ![]() - правильний трикутник, площина якого перпендикулярна площині основи. Знайдіть кут нахилу грані
- правильний трикутник, площина якого перпендикулярна площині основи. Знайдіть кут нахилу грані ![]() до основи.
до основи.
Розв’язання:
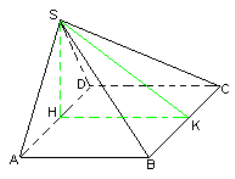 Розглянемо піраміду
Розглянемо піраміду ![]() .
. ![]() - квадрат. Грань
- квадрат. Грань ![]() - правильний трикутник,
- правильний трикутник, ![]() , де
, де ![]() - висота трикутника
- висота трикутника ![]() . Проведемо
. Проведемо ![]() , оскільки
, оскільки ![]() , то
, то ![]() .
. ![]() - похила,
- похила, ![]() - її проекція, тоді за теоремою про три перпендикуляри
- її проекція, тоді за теоремою про три перпендикуляри ![]() .
. ![]() - шуканий кут (лінійний кут двогранного кута). Нехай
- шуканий кут (лінійний кут двогранного кута). Нехай ![]() . З
. З ![]() :
: ![]() . З
. З ![]() :
: ![]() .
.
 Відповідь:
Відповідь: ![]() .
.
37. Побудувати графік функції: ![]() .
.
Розв’язання:
Необхідно: ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
38. Знайдіть всі значення параметра ![]() , при яких нерівність
, при яких нерівність ![]() виконується для всіх дійсних значень
виконується для всіх дійсних значень ![]() .
.
Розв’язання:
Зробимо заміну ![]() . Розглянемо функцію
. Розглянемо функцію ![]() .
.
Необхідно знайти всі ![]() , при яких
, при яких ![]() для всіх
для всіх ![]() . (1)
. (1)
Якщо ![]() , то умова (1) не виконується.
, то умова (1) не виконується.
Якщо ![]() , то
, то ![]() . Умова (1) не виконується.
. Умова (1) не виконується.
Нехай ![]() . За умови
. За умови ![]() умова (1) виконується. Отже,
умова (1) виконується. Отже, ![]() .
.
Якщо ![]() , то при
, то при ![]()
![]() для всіх
для всіх ![]() ;
;
при ![]()
![]() для всіх
для всіх ![]() . Отже,
. Отже, ![]() - розв’язки.
- розв’язки.
 Якщо
Якщо ![]() , то графік функції
, то графік функції ![]() має дві точки перетину з віссю абсцис. На малюнку зображено ситуацію, при якій виконується умова (1). Цьому малюнку відповідає система:
має дві точки перетину з віссю абсцис. На малюнку зображено ситуацію, при якій виконується умова (1). Цьому малюнку відповідає система:  .
.
Відповідь: ![]() .
.
Варіант 15 (2008 рік)
36. Дано пряму чотирикутну призму ![]() , в основі якої лежить ромб
, в основі якої лежить ромб ![]() зі стороною
зі стороною ![]() і гострим кутом
і гострим кутом ![]() . Висота призми дорівнює
. Висота призми дорівнює ![]() . Точки
. Точки ![]() і
і ![]() лежать на сторонах
лежать на сторонах ![]() і
і ![]() відповідно, причому
відповідно, причому ![]() . Точка
. Точка ![]() - точка перетину діагоналей призми. Через точки
- точка перетину діагоналей призми. Через точки ![]() проведено переріз призми. Знайти його площу.
проведено переріз призми. Знайти його площу.
Розв’язання:

![]() та
та ![]() подібні за двома сторонами
подібні за двома сторонами ![]() і спільним кутом
і спільним кутом ![]() . Нехай
. Нехай ![]() , оскільки
, оскільки ![]() як діагоналі ромба і
як діагоналі ромба і ![]() . Через точки
. Через точки ![]() і
і ![]() проводимо пряму до перетину з
проводимо пряму до перетину з ![]() . Отримаємо точку
. Отримаємо точку ![]() через яку проводимо
через яку проводимо ![]() , де
, де ![]() ;
; ![]() . Через точку
. Через точку ![]() в площині діагонального перерізу
в площині діагонального перерізу ![]() проводимо
проводимо ![]() , де
, де ![]() ;
; ![]() . Шестикутник
. Шестикутник ![]() - переріз призми, площу якого треба знайти. Цей шестикутник складається з двох рівних між собою трапецій, тому
- переріз призми, площу якого треба знайти. Цей шестикутник складається з двох рівних між собою трапецій, тому ![]() . З
. З ![]() , тоді
, тоді ![]() ;
; ![]() ;
; ![]() . З
. З ![]() , отже шукана площа
, отже шукана площа ![]() .
.
Відповідь: ![]()
 37. Побудувати графік рівняння
37. Побудувати графік рівняння ![]() .
.
Розв’язання:
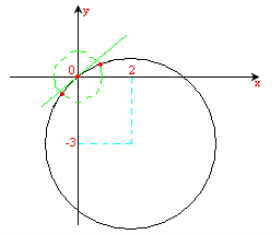
Область допустимих значень:  . На ОДЗ рівняння еквівалентне наступному
. На ОДЗ рівняння еквівалентне наступному ![]() . Графіком рівняння буде коло з центром в точці (2;-3) і радіусом
. Графіком рівняння буде коло з центром в точці (2;-3) і радіусом ![]() , з якого вилучено точки (0;0) і точки перетину цього кола з колом, яке має центр в точці (0;0) і радіус 1. Відстань від центра кола (точки (2;-3)) до прямої
, з якого вилучено точки (0;0) і точки перетину цього кола з колом, яке має центр в точці (0;0) і радіус 1. Відстань від центра кола (точки (2;-3)) до прямої ![]() дорівнює
дорівнює 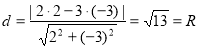 , отже пряма є дотичною до кола, тому нерівність
, отже пряма є дотичною до кола, тому нерівність ![]() виконується.
виконується.
38. При всіх значеннях параметра ![]() розв’язати нерівність
розв’язати нерівність![]() . Знайти всі
. Знайти всі ![]() , при кожному з яких розв’язком нерівності є відрізок довжини 2.
, при кожному з яких розв’язком нерівності є відрізок довжини 2.
Розв’язання:
Необхідними є умови ![]() .
.
Якщо ![]() , то нерівність
, то нерівність ![]() виконується при
виконується при ![]() . Тому необхідно, щоб
. Тому необхідно, щоб ![]() .
. ![]() . Таким чином, на множині
. Таким чином, на множині ![]()
![]() .
.
Якщо ![]() , то нерівність
, то нерівність![]() виконується. Тому розв’язком даної нерівності буде відрізок
виконується. Тому розв’язком даної нерівності буде відрізок  .
.
Необхідно знайти всі ![]() для яких довжина цього відрізка дорівнює 2. Отже,
для яких довжина цього відрізка дорівнює 2. Отже, ![]() ;
; ![]() ;
; ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то  . При
. При ![]() розв’язком нерівності буде відрізок довжини 2.
розв’язком нерівності буде відрізок довжини 2.
Варіант 16 (2008 рік)
36. Дано куб ![]() . Точка
. Точка ![]() є серединою ребра
є серединою ребра ![]() . Знайдіть площу перерізу куба площиною, яка проходить через точки
. Знайдіть площу перерізу куба площиною, яка проходить через точки ![]() , якщо ребро куба дорівнює
, якщо ребро куба дорівнює ![]() .
.
Розв’язання:
 Побудуємо переріз. В площині
Побудуємо переріз. В площині ![]() проводимо прямі
проводимо прямі ![]() та
та ![]() . Отримаємо
. Отримаємо ![]() . В площині
. В площині ![]() проводимо пряму
проводимо пряму![]() . Отримаємо
. Отримаємо ![]() .
. ![]() - за умовою;
- за умовою; ![]() - як вертикальні і трикутники прямокутні). Отже,
- як вертикальні і трикутники прямокутні). Отже, ![]() і оскільки
і оскільки ![]() , то
, то ![]() - середня лінія трикутника
- середня лінія трикутника ![]() . Таким чином, точка
. Таким чином, точка ![]() - середина
- середина ![]() . Чотирикутник
. Чотирикутник ![]() - переріз, площу якого треба знайти. Він складається з двох трикутників:
- переріз, площу якого треба знайти. Він складається з двох трикутників: ![]() та
та ![]() .
.
Введемо прямокутну декартову систему координат: центр – точка ![]() ; вісі координат збігаються з напрямками векторів
; вісі координат збігаються з напрямками векторів ![]() відповідно. В цій системі
відповідно. В цій системі ![]() . Тоді
. Тоді  .
.
Точка ![]() , тоді
, тоді ![]() .
.  .
.
Шукана площа: ![]() .
.
Відповідь: ![]() .
.
37. Побудуйте графік функції: ![]() .
.
Розв’язання:
 Якщо
Якщо ![]() , то функція невизначена.
, то функція невизначена.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
38. Розв’яжіть нерівність: ![]() .
.
Розв’язання:
ОДЗ:![]() . Очевидно, що при
. Очевидно, що при ![]()
![]() . Необхідно, щоб
. Необхідно, щоб ![]() . Отже, при
. Отже, при ![]() .
.
При ![]()
![]() . Необхідно, щоб
. Необхідно, щоб ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
 Варіант 17 (2008 рік)
Варіант 17 (2008 рік)
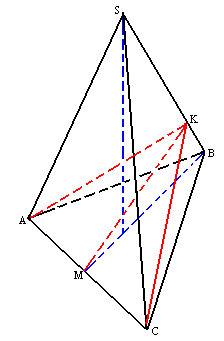
36. Дано правильну трикутну піраміду ![]() , причому
, причому ![]() - вершина, трикутник
- вершина, трикутник ![]() - основа. Нехай сторона основи дорівнює
- основа. Нехай сторона основи дорівнює ![]() , бічне ребро
, бічне ребро ![]() . Через сторону основи
. Через сторону основи ![]() проведено переріз
проведено переріз ![]() найменшої площі
найменшої площі ![]() . Знайдіть:
. Знайдіть:
-
Відношення
 ;
;
- Площу перерізу;
-
Кут
 між площиною перерізу і площиною основи цієї піраміди.
між площиною перерізу і площиною основи цієї піраміди.
Розв’язання:
-
Нехай
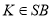 . Трикутник
. Трикутник  - рівнобедрений, тому медіана
- рівнобедрений, тому медіана  є висотою. Очевидно, що найменша площа
є висотою. Очевидно, що найменша площа  буде тоді, коли відстань від точки
буде тоді, коли відстань від точки  до
до  буде найменшою, тобто
буде найменшою, тобто 
 . Нехай
. Нехай  кут при основі рівнобедреного трикутника
кут при основі рівнобедреного трикутника 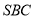 , тоді
, тоді 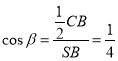 . З
. З  , тоді
, тоді 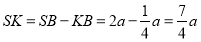 і
і  .
.
-
 , тоді
, тоді  . З
. З 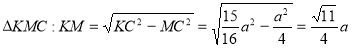

 .
.
-
З
 .
.
Відповідь: a)![]() ; b)
; b) ![]() ; c)
; c) ![]() .
.
37. Побудувати графік функції ![]() .
.
 Розв’язання:
Розв’язання:
![]()
Якщо ![]() , то функція невизначена.
, то функція невизначена.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
![]() .
.
38. Розв’язати систему рівнянь:  .
.
Розв’язання:
 Якщо
Якщо ![]() , то система має два розв’язки: (0;-2),(0;2).
, то система має два розв’язки: (0;-2),(0;2).
Якщо ![]() (мал. a), то
(мал. a), то ![]() .
.
Далі, ![]() . Пари (0;-2),(0;2) будуть розв’язками системи для довільних
. Пари (0;-2),(0;2) будуть розв’язками системи для довільних ![]() .
.
Припустимо, що система має деякий розв’язок ![]() , тоді в силу парності обох рівнянь відносно обох змінних, система буде мати розв’язки
, тоді в силу парності обох рівнянь відносно обох змінних, система буде мати розв’язки ![]() . На малюнках b, c показано ситуації при
. На малюнках b, c показано ситуації при ![]() та
та ![]() відповідно.
відповідно.
Нехай ![]() . З другого рівняння
. З другого рівняння ![]() , тоді в першому рівнянні
, тоді в першому рівнянні ![]() , тоді
, тоді ![]() .
.
Відповідь: при ![]() : (0;-2), (0;2); при
: (0;-2), (0;2); при ![]() :
: ![]() ; при
; при ![]() :
:  ;
; 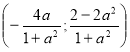 ;
;  ;
;  ; (0; -2); (0; 2).
; (0; -2); (0; 2).
Варіант 18 (2008 рік)
 36. Бічне ребро правильної трикутної піраміди удвічі більше за сторону основи і дорівнює
36. Бічне ребро правильної трикутної піраміди удвічі більше за сторону основи і дорівнює ![]() . Через центр основи паралельно одній із бічних граней проведено площину.
. Через центр основи паралельно одній із бічних граней проведено площину.
- Побудуйте цей переріз та з’ясуйте, якою геометричною фігурою він є.
-
Знайдіть кут
 між площиною основи піраміди та перерізом.
між площиною основи піраміди та перерізом.
-
Знайдіть площу
 перерізу.
перерізу.
Розв’язання:
-
a) Нехай
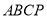 - правильна трикутна піраміда,
- правильна трикутна піраміда,  - вершина;
- вершина;  - основа;
- основа;  - центр основи (проекція вершини на основу). Проведемо апофему
- центр основи (проекція вершини на основу). Проведемо апофему  бічної грані
бічної грані  . В площині
. В площині  через точку
через точку  проведемо
проведемо 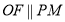 (
(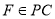 ) . В гранях
) . В гранях 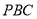 та
та  проводимо
проводимо 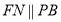 та
та 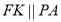 відповідно. Точки
відповідно. Точки 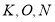 лежать на одній прямій, оскільки
лежать на одній прямій, оскільки 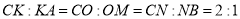 . Рівнобедрений трикутник
. Рівнобедрений трикутник  - шуканий переріз. Причому
- шуканий переріз. Причому  подібний
подібний  і
і  .
.
-
Оскільки
 , то шуканий кут дорівнює куту нахилу бічної грані до основи.
, то шуканий кут дорівнює куту нахилу бічної грані до основи.  .
. 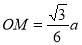 (радіус кола, вписаного в правильний трикутник зі стороною
(радіус кола, вписаного в правильний трикутник зі стороною  );
); 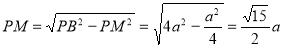 , отже
, отже  .
.
-
Оскільки
 подібний
подібний  і коефіцієнт подібності
і коефіцієнт подібності  , то
, то  .
.
Відповідь: a) рівнобедрений трикутник, подібний бічній грані з коефіцієнтом ![]() і паралельний їй; b)
і паралельний їй; b) ![]() ; с)
; с) ![]() .
.
37. Побудуйте графік функції  .
.
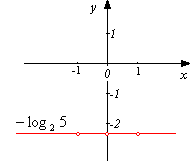 Розв’язання:
Розв’язання:
ОДЗ: ![]() . Функція парна. Зробимо перетворення:
. Функція парна. Зробимо перетворення: ![]() .
.
38. Розв’яжіть нерівність: ![]() .
.
Розв’язання:
Покладемо ![]() .
. ![]() ;
; ![]() ;
; ![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() .
.
При ![]() нерівність розв’язків немає.
нерівність розв’язків немає.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ;
;
 якщо
якщо ![]() , то
, то ![]() .
.
Варіант 19 (2008 рік)
36. Основою прямого паралелепіпеда ![]() є квадрат
є квадрат ![]() зі стороною 2 см. Бічне ребро паралелепіпеда дорівнює 6 см. Знайдіть кут
зі стороною 2 см. Бічне ребро паралелепіпеда дорівнює 6 см. Знайдіть кут ![]() між медіаною трикутника
між медіаною трикутника ![]() , проведеною з вершини
, проведеною з вершини ![]() , і діагональним перерізом паралелепіпеда
, і діагональним перерізом паралелепіпеда ![]() .
.
Розв’язання:
Проведемо медіану ![]()
![]() . В площині
. В площині ![]() проведемо
проведемо ![]() . Площини
. Площини ![]() та
та ![]() перпендикулярні, тому
перпендикулярні, тому ![]() .
. ![]() проекція похилої
проекція похилої ![]() на площину
на площину ![]() . Таким чином,
. Таким чином, ![]() .
.
З ![]() .
.
З ![]() .
.
![]() .
.
Відповідь: ![]() .
.
37. Побудувати графік рівняння: ![]()
Розв’язання:
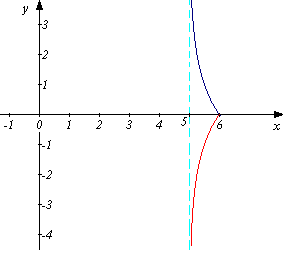
38. Розв’яжіть рівняння: ![]() .
.
Розв’язання:
Оскільки ![]() і
і ![]() , то рівняння можна записати у вигляді:
, то рівняння можна записати у вигляді:  . З другого рівняння маємо
. З другого рівняння маємо ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ;
; ![]() .
.
Варіант 20. (ЗНО – 2007)
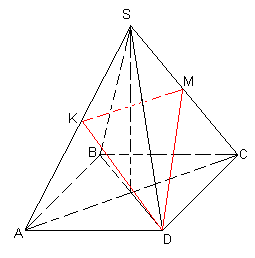 36. У правильній чотирикутній піраміді
36. У правильній чотирикутній піраміді ![]() (
(![]() - вершина) бічне ребро вдвічі більше сторони основи. Знайдіть кут між медіаною трикутника
- вершина) бічне ребро вдвічі більше сторони основи. Знайдіть кут між медіаною трикутника ![]() , проведеною з вершини
, проведеною з вершини ![]() , та середньою лінією трикутника
, та середньою лінією трикутника ![]() , що паралельна основі піраміди.
, що паралельна основі піраміди.
Розв’язання:
![]() - правильна чотирикутна піраміда. Нехай
- правильна чотирикутна піраміда. Нехай ![]() , тоді
, тоді ![]() .
.
![]() за трьома сторонами, тому
за трьома сторонами, тому ![]() (відповідні елементи рівних фігур – рівні).
(відповідні елементи рівних фігур – рівні).
З ![]() .
. ![]() .
.
З ![]() .
.
![]() - середня лінія
- середня лінія ![]() , тому
, тому ![]() .
.
Нехай ![]() (шуканий кут), тоді з рівнобедреного
(шуканий кут), тоді з рівнобедреного ![]()
Відповідь: ![]()
37. Побудуйте графік функції: ![]()
Розв’язання:
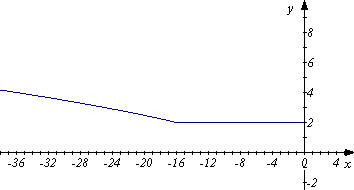 ОДЗ:
ОДЗ: ![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
38. Розв’яжіть нерівність: ![]()
Розв’язання:
Необхідно: ![]()
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() . Необхідно, щоб
. Необхідно, щоб ![]() .
. ![]() , тоді остання нерівність має розв’язки:
, тоді остання нерівність має розв’язки: ![]() .
.
Якщо ![]() , то
, то ![]() , бо
, бо ![]() . Необхідно, щоб
. Необхідно, щоб ![]()
![]()
![]() .
.
 Відповідь: при
Відповідь: при ![]() нерівність невизначена; при
нерівність невизначена; при ![]()
![]() ; при
; при ![]()
![]() ; при
; при ![]()
![]() .
.
Варіант 21 (ЗНО – 2008)
34. У правильній трикутній піраміді ![]() з основою
з основою ![]() бічне ребро вдвічі більше за сторону основи. Точки
бічне ребро вдвічі більше за сторону основи. Точки ![]() і
і ![]() є серединами ребер
є серединами ребер ![]() і
і ![]() відповідно. Через пряму
відповідно. Через пряму ![]() , паралельно до ребра
, паралельно до ребра ![]() , проведено площину
, проведено площину ![]() . Знайдіть кут
. Знайдіть кут ![]() між площиною
між площиною ![]() і площиною
і площиною ![]() .
.
Розв’язання:
Нехай ![]() , де
, де ![]() - висота
- висота ![]()
В гранях ![]() та
та ![]() проводимо
проводимо ![]() та
та ![]() відповідно. Площина
відповідно. Площина ![]() - це площина, в якій лежить чотирикутник
- це площина, в якій лежить чотирикутник ![]() . Точка
. Точка ![]() - точка перетину площини
- точка перетину площини ![]() з висотою
з висотою ![]() піраміди. Ребро
піраміди. Ребро ![]() , отже, шуканий кут
, отже, шуканий кут ![]() - це кут нахилу бічного ребра до основи. Покладемо
- це кут нахилу бічного ребра до основи. Покладемо ![]() - сторона основи, тоді
- сторона основи, тоді ![]() , тоді
, тоді ![]() .
.
Відповідь: ![]() .
.
35. Розв’яжіть систему нерівностей: 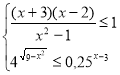
Розв’язання:
 Розв’язуємо першу нерівність.
Розв’язуємо першу нерівність. ![]() .
.
Розв’язуємо другу нерівність. Для неї
ОДЗ: ![]() . На ОДЗ друга нерівність еквівалентна наступній:
. На ОДЗ друга нерівність еквівалентна наступній:![]() . Підносимо до квадрату.
. Підносимо до квадрату. ![]() .
.
Враховуючі ОДЗ і «картинку-розв’язок» для першої нерівності, отримаємо:

Відповідь: ![]() .
.
36. Задано функцію ![]() .
.
- Знайдіть проміжки зростання та спадання функції, екстремуми функції.
-
Побудуйте ескіз графіка функції
 .
.
-
Знайдіть кількість коренів рівняння
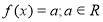 , залежно від значень параметра
, залежно від значень параметра  .
.
Розв’язання:
1. Знаходимо похідну: ![]()

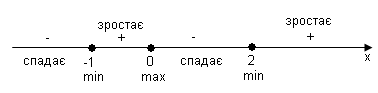
2. Проводимо прямі ![]() і «знімаємо» з графіка функції відповідь.
і «знімаємо» з графіка функції відповідь.
Відповідь: 1) ![]() та
та ![]() - проміжки спадання;
- проміжки спадання; ![]() та
та ![]() - проміжки зростання;
- проміжки зростання; ![]() та
та ![]() - точки мінімуму;
- точки мінімуму; ![]() - точка максимуму.
- точка максимуму.
3) ![]() - розв’язків немає;
- розв’язків немає;
![]() - один розв’язок;
- один розв’язок;
![]() - два розв’язки;
- два розв’язки;
![]() або
або ![]() - три розв’язки;
- три розв’язки;
![]() - чотири розв’язки.
- чотири розв’язки.
Варіант 22 (пробне ЗНО – 2009)
31. Основою піраміди є рівносторонній трикутник зі стороною ![]() . Одна з бічних граней перпендикулярна до площини основи, а дві інші – нахилені до основи під кутом
. Одна з бічних граней перпендикулярна до площини основи, а дві інші – нахилені до основи під кутом ![]() . Знайдіть об'єм піраміди.
. Знайдіть об'єм піраміди.
Розв’язання:
 Розглянемо трикутну піраміду
Розглянемо трикутну піраміду ![]() , у якої
, у якої ![]() . Отже,
. Отже, ![]() - висота і медіана рівнобедреного трикутника
- висота і медіана рівнобедреного трикутника ![]() є висотою піраміди. Проводимо
є висотою піраміди. Проводимо ![]() ,
, ![]() - похила,
- похила, ![]() - її проекція, тому
- її проекція, тому ![]() (теорема про три перпендикуляри).
(теорема про три перпендикуляри). ![]() (лінійний кут двогранного кута).
(лінійний кут двогранного кута).
-
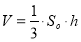
-

-
З

-
З
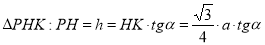
-
Підставляємо 2) та 4) в 1):

Відповідь: ![]()
32. На лузі біля річки треба обгородити ділянку прямокутної форми, що прилягає до прямолінійного берега річки (з боку річки огорожа не встановлюється). Завезено 200 погонних метрів огорожі. Якими повинні бути розміри відповідного прямокутника, щоб його площа була найбільшою?
Розв’язання:
 Позначимо
Позначимо ![]() , тоді
, тоді ![]() . Розглянемо функцію:
. Розглянемо функцію: ![]() , яку досліджуємо на максимум.
, яку досліджуємо на максимум.
![]() - критична точка
- критична точка
![]() - точка максимуму.
- точка максимуму.
Відповідь: 50; 50 та 100
33. Задано функцію ![]() . Знайдіть:
. Знайдіть:
-
Область визначення функції
 .
.
-
Нулі функції
 .
.
-
Усі розв’язки нерівності
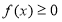
Розв’язання:
-
Необхідно:

-
За умови
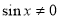 отримаємо рівняння-наслідок
отримаємо рівняння-наслідок 
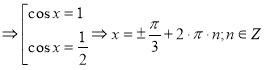 . Зауважимо, що перше рівняння сукупності розв’язків не дає , бо за умови
. Зауважимо, що перше рівняння сукупності розв’язків не дає , бо за умови  маємо
маємо  .
.
-
 Користуючись пунктом б), запишемо нерівність у вигляді:
Користуючись пунктом б), запишемо нерівність у вигляді: 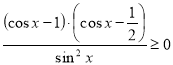 . На ОДЗ маємо
. На ОДЗ маємо 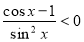 . Тому для виконання нерівності необхідно і достатньо:
. Тому для виконання нерівності необхідно і достатньо:  . На малюнку зображено дугу, яка відповідає останній нерівності.
. На малюнку зображено дугу, яка відповідає останній нерівності.
Відповідь:
 Варіант 23 (ЗНО – 2009)
Варіант 23 (ЗНО – 2009)
31. Радіус основи конуса ![]() , твірна нахилена до площини основи під кутом α. Через вершину конуса проведено площину під кутом φ до його висоти. Ця площина перетинає основу конуса по хорді. Знайдіть площу утвореного перерізу.
, твірна нахилена до площини основи під кутом α. Через вершину конуса проведено площину під кутом φ до його висоти. Ця площина перетинає основу конуса по хорді. Знайдіть площу утвореного перерізу.
Розв’язання:
Розглянемо конус, в якому проведено переріз ![]() . Цей переріз – рівнобедрений трикутник
. Цей переріз – рівнобедрений трикутник ![]() , як твірні конуса).
, як твірні конуса). ![]() , де
, де ![]() - центр основи конуса (
- центр основи конуса (![]() - проекція
- проекція ![]() на площину основи). Проведемо
на площину основи). Проведемо ![]() , тоді
, тоді ![]() - це кут між площиною перерізу і висотою
- це кут між площиною перерізу і висотою ![]() конуса (
конуса (![]() - проекція
- проекція ![]() на цю площину).
на цю площину).
-
З
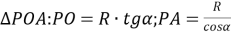
-
З

-
 - прямокутний (
- прямокутний ( - проекція
- проекція  на основу,
на основу,  , тоді за теоремою про три перпендикуляри
, тоді за теоремою про три перпендикуляри 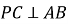 ). За теоремою Піфагора:
). За теоремою Піфагора: 
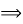

-
Шукана площа:
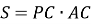
Відповідь: ![]()
-
Задано функції
 і
і  .
.
-
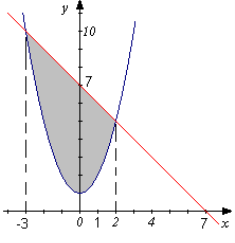 Знайдіть абсциси точок перетину графіків функцій
Знайдіть абсциси точок перетину графіків функцій  і
і  . У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
. У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
-
Обчисліть площу фігури, обмеженої графіками функцій
 і
і  .
.
Розв’язання:
-
Для знаходження абсцис точок перетину розв’язуємо рівняння:
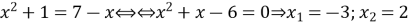 .
.
-

![]()
![]()
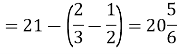
Відповідь: 1) ![]() - абсциси точок перетину графіків; 2)
- абсциси точок перетину графіків; 2) ![]() - площа фігури, що обмежена графіками функцій.
- площа фігури, що обмежена графіками функцій.
33. Розв’яжіть нерівність ![]()
Розв’язання:
-
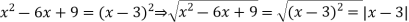
-

-
 Нерівність можна записати у вигляді:
Нерівність можна записати у вигляді: 
![]() . Отже, на цій множині розв’язків немає.
. Отже, на цій множині розв’язків немає.
-
 . Отже, розв’язком є множина:
. Отже, розв’язком є множина: 
-
 - розв’язок даної нерівності.
- розв’язок даної нерівності.
![]() :
: ![]()
Варіант 24 (пробне ЗНО – 2010)
-
 Знайдіть найбільше значення параметра a, при якому рівняння
Знайдіть найбільше значення параметра a, при якому рівняння 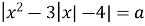 має чотири корені. Якщо такого значення не існує, то у відповідь запишіть число 100.
має чотири корені. Якщо такого значення не існує, то у відповідь запишіть число 100.
Розв’язання:
Будуємо графік функції ![]() . Проводимо прямі
. Проводимо прямі ![]() .
.
Відповідь: 6,25
-
У правильну чотирикутну піраміду вписано сферу, площа якої дорівнює
 см2. Бічна грань піраміди нахилена до площини її основи під кутом 60. Знайдіть об'єм піраміди (у см3)
см2. Бічна грань піраміди нахилена до площини її основи під кутом 60. Знайдіть об'єм піраміди (у см3)
 Розв’язання:
Розв’язання:
Розглянемо піраміду PABCD. Висота піраміди PK. Центр вписаної сфери ![]() .
. ![]() – проекція
– проекція ![]() на основу, тому
на основу, тому ![]() (теорема про три перпендикуляри).
(теорема про три перпендикуляри). ![]() (лінійний кут двогранного кута). Для
(лінійний кут двогранного кута). Для ![]() є бісектрисою
є бісектрисою ![]() .
. ![]()
Площа сфери: ![]() , тому
, тому ![]()
З ![]() ; з
; з ![]() .
.
Шуканий об'єм піраміди: ![]()
Відповідь: 324
Варіант 25 (ЗНО – 2010, І сесія)
35. Основою піраміди є ромб, гострий кут якого дорівнює 30°. Усі бічні грані піраміди нахилені до площини її основи під кутом 60°. Знайдіть площу бічної поверхні піраміди (у см2), якщо радіус кола, вписаного в її основу дорівнює: 3 см, 4 см, 2 см.
 Розв’ьязання:
Розв’ьязання:
PABCD – дана піраміда. PO – висота піраміди, ОК – радіус основи (![]() . ОК – проекція РК на основу, тому
. ОК – проекція РК на основу, тому ![]() (теорема про три перпендикуляри).
(теорема про три перпендикуляри). ![]() (лінійний кут двогранного кута).
(лінійний кут двогранного кута).
З ![]() ;
;
З ![]() .
.
![]()
![]()
![]()
![]()
36. Розв’яжіть систему. Якщо система має єдиний розв’язок ![]() , то у відповідь запишіть суму
, то у відповідь запишіть суму ![]() ; якщо система має більше, ніж один розв’язок, то у відповідь запишіть кількість усіх розв’язків.
; якщо система має більше, ніж один розв’язок, то у відповідь запишіть кількість усіх розв’язків.

Розв’язання:
В правій частині виділяємо повний квадрат: ![]() . Маємо: найбільше значення лівої частини співпадає з найменшим значенням правої.
. Маємо: найбільше значення лівої частини співпадає з найменшим значенням правої.
![]()
Для другої системи: ![]()
Для третьої системи: ![]()
Відповідь: -12 10 14
Варіант 26 (ЗНО – 2010, ІІ сесія)
 35. Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює
35. Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює ![]() см, гострий кут – 30°. Усі бічні ребра піраміди нахилені до площини її основи під кутом 45°. Знайдіть об’єм піраміди ( у см3).
см, гострий кут – 30°. Усі бічні ребра піраміди нахилені до площини її основи під кутом 45°. Знайдіть об’єм піраміди ( у см3).
Розв’язання:
Оскільки всі бічні ребра піраміди нахилені до основи під одним кутом, то вершина проектується в центр описаного кола. Центр кола, описаного навколо прямокутного трикутника – середина гіпотенузи. АО = ОВ = ![]() .
.
З ![]() :
: ![]()
З ![]()
![]()
Відповідь: 12
-
Розв’яжіть рівняння:
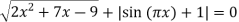 . Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів.
. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів.
Розв’язання:
Сума двох невід’ємних виразів дорівнює нулю тоді і тільки тоді, коли кожен з них дорівнює нулю.
![]()
-
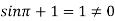 2)
2) 
Відповідь: -4,5
Варіант 27 (пробне ЗНО – 2011)
- В основі піраміди лежить прямокутний трикутник із кутом 15°. Усі бічні ребра піраміди нахилені до площини основи під кутом 60°. Радіус кулі, описаної навколо піраміди, дорівнює 6 см. Обчисліть об’єм піраміди ( у см3).
Розв’язання:
 Оскільки всі бічні ребра піраміди нахилені до основи під одним кутом, то вершина піраміди проектується в центр описаного навколо основи кола. Це – середина гіпотенузи. Центр описаної кулі належить висоті PH піраміди.
Оскільки всі бічні ребра піраміди нахилені до основи під одним кутом, то вершина піраміди проектується в центр описаного навколо основи кола. Це – середина гіпотенузи. Центр описаної кулі належить висоті PH піраміди. ![]() – рівносторонній, тому
– рівносторонній, тому ![]()
![]()
З ![]() , тоді
, тоді
![]() =
=![]()
![]()
Відповідь: 40,5
-
Укажіть найменше значення
 , при якому рівняння
, при якому рівняння  має рівно один корінь.
має рівно один корінь.
Розв’язання:
Чисельник має один корінь, якщо ![]()
Знайдемо корені чисельника, за умови: ![]()
![]() . Дане рівняння має один корінь, якщо
. Дане рівняння має один корінь, якщо ![]() або
або ![]()
Відповідь: -3,75
Варіант 28 (ЗНО – 2011)
- Двоє робітників, працюючи разом, можуть скосити траву на ділянці за 2 години 6 хвилин. Скільки часу (у годинах) витратить на скошування трави на цій ділянці другий робітник, якщо йому потрібно на виконання цього завдання на 4 години більше, ніж першому робітникові?
Розв’язання:
Нехай a годин треба першому робітнику, тоді (a + 4) годин треба другому робітнику. Працюючи разом вони витратять ![]() годин. Маємо рівняння:
годин. Маємо рівняння:
![]() ;
; ![]()
Відповідь: 7
-
У чотирикутну піраміду, в основі якої лежить рівнобічна трапеція з бічною стороною 13 см і основами 8 см і 18 см, вписано конус. Знайдіть площу бічної поверхні конуса
 ( у см2), якщо всі бічні грані піраміди нахилені до площини основи під кутом 60°. У відповідь запишіть значення
( у см2), якщо всі бічні грані піраміди нахилені до площини основи під кутом 60°. У відповідь запишіть значення 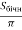
Розв’язання:
 В трапецію ABCD можна вписати коло, тому
В трапецію ABCD можна вписати коло, тому ![]() ;
; ![]() . Проводимо висоту
. Проводимо висоту ![]() .
.
З ![]() . Радіус основи вписаного конуса
. Радіус основи вписаного конуса ![]() , тоді його твірна
, тоді його твірна ![]()
![]()
Відповідь: 72
-
На рисунку зображено графік функції
 , що визначена на проміжку
, що визначена на проміжку  і має лише три нулі. Розв’яжіть систему:
і має лише три нулі. Розв’яжіть систему:  . У відповідь запишіть суму всіх цілих розв’язків системи.
. У відповідь запишіть суму всіх цілих розв’язків системи.
 Розв’язання:
Розв’язання:
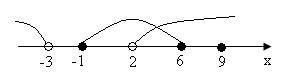
![]()
![]()
Відповідь: 27
-
Знайдіть найменше значення
 , при якому має розв’язки рівняння
, при якому має розв’язки рівняння
![]() .
.
Розв’язання:
![]()
![]()
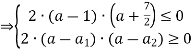 , де
, де ![]()

![]()
Відповідь: -3,5
Варіант 29 (пробне ЗНО – 2012)
- Навколо правильної трикутної призми описано сферу радіуса 6 см. Радіус сфери, проведений до вершини призми, утворює з бічним ребром кут 30°. Визначте об'єм призми.
Розв’язання:
Центр описаної кулі – точка ![]() , де
, де ![]() – відрізок, що з’єднує центри нижньої та верхньої основ призми, причому О – середина
– відрізок, що з’єднує центри нижньої та верхньої основ призми, причому О – середина ![]() , оскільки вона рівновіддалена від всіх вершин призми.
, оскільки вона рівновіддалена від всіх вершин призми.
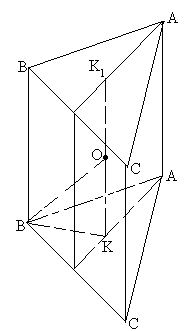 З
З ![]()
З ![]()
![]()
Відповідь: 121,5
-
Знайдіть усі значення параметра а , при яких добуток коренів рівняння
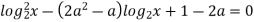 дорівнює 8. Якщо таке значення одне, то запишіть його у відповідь. Якщо таких значень більше одного, то у відповідь запишіть найменше з них.
дорівнює 8. Якщо таке значення одне, то запишіть його у відповідь. Якщо таких значень більше одного, то у відповідь запишіть найменше з них.
Розв’язання:
Нехай ![]() .
.
Якщо ![]() – корені даного рівняння, то
– корені даного рівняння, то ![]() .
.
Для квадратного рівняння ![]() маємо:
маємо: ![]()
![]()
Перевірка: 1) ![]() 2)
2) ![]()
Відповідь: 1,5
Варіант 30 (ЗНО – 2012.Перша сесія)
31. Основою прямої призми ABCDA1B1C1D1 є рівнобічна трапеція ABCD. Основа AD трапеції дорівнює висоті трапеції і в шість разів більша за основу ВС. Через бічне ребро СС1 проведено площину паралельну ребру АВ. Знайдіть площу утвореного перерізу ( у см2), якщо
|
|
І варіант |
ІІ варіант |
ІІІ варіант |
|
Об'єм призми |
672 см3 |
588 см3 |
756 см3 |
|
Висота призми |
8 см |
7 см |
9 см |
 Розв’язання:
Розв’язання:
Нехай V – об'єм призми, h – висота призми. Проведемо ![]() , площу якого необхідно знайти.
, площу якого необхідно знайти.
-
1)
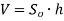 ; 2)
; 2) 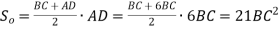
-
3)
 ; 4) для
; 4) для  , але
, але
-
 , тому
, тому
-

-
4)

-
І варіант:

-
ІІ варіант:

ІІІ варіант: ![]()
Відповідь: 104 91 117
32.При якому найменшому цілому значенні параметра ![]() рівняння має лише два різні корені?
рівняння має лише два різні корені?
|
І варіант |
|
|
ІІ варіант |
|
|
ІІІ варіант |
|
Розв’язання:
Запишемо рівняння у вигляді ![]()
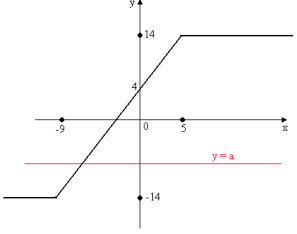 Один корінь
Один корінь ![]() рівняння має незалежно від значень параметра
рівняння має незалежно від значень параметра ![]() . Розглянемо рівняння
. Розглянемо рівняння ![]() (*) . Будуємо графік функції
(*) . Будуємо графік функції 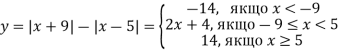
Отже, рівняння (*) має один корінь за умови ![]() . Цей корінь:
. Цей корінь: ![]() . Необхідно, щоб
. Необхідно, щоб ![]() . Найменше ціле значення, що задовольняє останню умову -10.
. Найменше ціле значення, що задовольняє останню умову -10.
Для другого варіанта: фіксований корінь ![]() . Другий корінь находимо з рівняння:
. Другий корінь находимо з рівняння:
![]()
![]()
Для третього варіанта: фіксований корінь ![]() . Другий корінь знаходимо з рівняння:
. Другий корінь знаходимо з рівняння: ![]()
![]()
Відповідь: -10 -11 -9
Варіант 31 (ЗНО – 2012. Друга сесія)
- Основою прямої трикутної призми АВСА1В1С1 є рівнобедрений трикутник АВС, де АВ = ВС = 25 см, АС = 30 см. Через бічне ребро АА1 проведено площину, перпендикулярну до ребра ВС. Визначте об’єм призми ( у см3), якщо площа утвореного перерізу
|
І варіант |
ІІ варіант |
ІІІ варіант |
|
72 см2 |
96 см2 |
48 см2 |
Розв’язання:
 Проведемо висоту ВМ до основи АС рівнобедреного трикутника АВС. Знаходимо площу основи. ВМ = 20 (числа 15, 20, 25 утворюють піфагорову трійку).
Проведемо висоту ВМ до основи АС рівнобедреного трикутника АВС. Знаходимо площу основи. ВМ = 20 (числа 15, 20, 25 утворюють піфагорову трійку). ![]() . Об'єм призми:
. Об'єм призми: ![]() , де
, де ![]() – висота призми.
– висота призми. ![]()
![]()
І варіант: ![]()
ІІ варіант: ![]()
ІІІ варіант: ![]()
Відповідь: 900 1200 600
-
При якому найменшому значенні параметра
 рівняння має хоча б один корінь?
рівняння має хоча б один корінь?
|
І варіант |
|
|
ІІ варіант |
|
|
ІІІ варіант |
|
Розв’язання:
![]() , тоді
, тоді ![]()
Нехай ![]() .
.
І варіант. ![]()
![]()
Необхідно, щоб ![]()
ІІ варіант. ![]()
=![]()
![]()
Необхідно, щоб ![]()
ІІІ варіант. ![]()
=![]()
Необхідно, щоб ![]()
Відповідь: 5,5 6,5 4,5
Варіант 32 (пробне ЗНО – 2013)
-
Основою прямої призми
 є ромб
є ромб 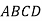 , у якому більша діагональ
, у якому більша діагональ  = 17 см. Об'єм призми дорівнює 1020 см3. Через діагональ
= 17 см. Об'єм призми дорівнює 1020 см3. Через діагональ  та вершину
та вершину  тупого кута верхньої основи призми проведено площину, яка утворює з площиною основи призми кут α. Знайдіть площу утвореного перерізу, якщо
тупого кута верхньої основи призми проведено площину, яка утворює з площиною основи призми кут α. Знайдіть площу утвореного перерізу, якщо  .
.
Розв’язання:
 Більша діагональ основи АС лежіть проти тупого кута В.
Більша діагональ основи АС лежіть проти тупого кута В. ![]() , як діагоналі ромба.
, як діагоналі ромба. ![]() – проекція
– проекція ![]() на основу, тому
на основу, тому ![]() (теорема про три перпендикуляри).
(теорема про три перпендикуляри). ![]() – лінійний кут двогранного кута.
– лінійний кут двогранного кута.
Нехай ![]() , тоді з
, тоді з ![]() ;
; ![]() . Але
. Але ![]() ,
, ![]() .
.
![]()
![]() .
.
-
Шукана площа:

- Відповідь: 110,5
-
Знайдіть найменше ціле значення параметра
 , при якому рівняння
, при якому рівняння  має два корені.
має два корені.
Розв’язання:
![]() .
. ![]() – корінь даного рівняння. Необхідно знайти найменше ціле значення параметра
– корінь даного рівняння. Необхідно знайти найменше ціле значення параметра ![]() , при якому рівняння
, при якому рівняння ![]() має корінь, причому
має корінь, причому ![]() . Розглянемо функцію
. Розглянемо функцію ![]() . Маємо:
. Маємо: ![]() . Далі
. Далі ![]() . Найменше ціле значення параметра, що задовольняє останню нерівність, дорівнює 11.
. Найменше ціле значення параметра, що задовольняє останню нерівність, дорівнює 11.
Відповідь: 11
Варіант 33 (ЗНО – 2013. Перша сесія)
32.Основою піраміди SABCD є трапеція ABCD (AD || BC), довжина середньої лінії якої дорівнює 5 см. Бічне ребро SB перпендикулярне до площини основи піраміди і вдвічі більше від середньої лінії трапеції ABCD. Знайдіть відстань від середини ребра SD до площини SBC (у см), якщо об'єм піраміди дорівнює V.
|
V |
210 см3 |
240 см3 |
180 см3 |
 Розв’язання:
Розв’язання:
ABCD – трапеція, площа якої ![]() .
.
Об'єм піраміди: ![]()
![]()
![]() – середина
– середина ![]() . Проводимо переріз піраміди, що проходить через точку
. Проводимо переріз піраміди, що проходить через точку ![]() , паралельно основі ABCD. Перерізом буде трапеція
, паралельно основі ABCD. Перерізом буде трапеція ![]() подібна до трапеції ABCD. Коефіцієнт подібності дорівнює
подібна до трапеції ABCD. Коефіцієнт подібності дорівнює ![]() . Шукана відстань дорівнює довжині висоти
. Шукана відстань дорівнює довжині висоти ![]() трапеції
трапеції ![]() .
.
![]()
Відповідь: 6,3 7,2 5,4
33.Знайдіть значення параметра ![]() , при якому корінь даного рівняння належить даному проміжку.
, при якому корінь даного рівняння належить даному проміжку.
|
Рівняння |
|
|
|
|
Проміжок |
|
|
|
Розв’язання:
Оскільки ![]() , то
, то ![]() . З іншого боку,
. З іншого боку, ![]() .
.
Маємо: ![]() . Для першого рівняння:
. Для першого рівняння: ![]()
І варіант: ![]()
IІ варіант: 1![]()
ІІІ варіант: ![]()
Відповідь: -14,3 -14,7 -23,3
Варіант 33 (ЗНО – 2013. Друга сесія)
- Основою піраміди є ромб, тупий кут якого дорівнює 120°. Дві бічні грані піраміди, що містять сторони цього кута, перпендикулярні до площини основи, а дві інші бічні грані нахилені до площини основи під кутом 30°. Знайдіть площу бічної поверхні піраміди (у см2), якщо її висота дорівнює h см.
|
h |
4 см |
3 см |
5 см |
Розв’язання:
 PABCD – дана піраміда, ABCD – ромб,
PABCD – дана піраміда, ABCD – ромб, ![]() ,
, ![]() .
.
Проведемо ![]() , BK – проекція похилої РК на основу, тому
, BK – проекція похилої РК на основу, тому ![]() (теорема про три перпендикуляри),
(теорема про три перпендикуляри), ![]() (лінійний кут двогранного кута)
(лінійний кут двогранного кута)
З ![]()
З ![]()
![]()
- Відповідь: 96 54 150
-
33. При якому найбільшому від’ємному значенні параметра
 дане рівняння має один корінь?
дане рівняння має один корінь?
|
|
|
|
Розв’язання:
Розглянемо рівняння: ![]() . Побудуємо графічні образи (
. Побудуємо графічні образи (![]()
 Необхідно, щоб графік функції
Необхідно, щоб графік функції ![]() став дотичною до графіка функції
став дотичною до графіка функції ![]() . Це можливо за умови
. Це можливо за умови ![]()
![]() , тобто саме в цій точці треба провести дотичну. Маємо:
, тобто саме в цій точці треба провести дотичну. Маємо: ![]()
Якщо ![]() , то
, то ![]()
Відповідь: -1,625 -3,625 -5,625
 Варіант 33 (пробне ЗНО – 2014)
Варіант 33 (пробне ЗНО – 2014)
32. Основою піраміди SABCD є трапеція ABCD (BC || AD). Бічна грань SBC, площа якої дорівнює 24,4 см2, перпендикулярна до площини основи піраміди. Точка М – середина ребра SB. Площина (MAD) перетинає ребро SC в точці N. Визначте довжину відрізка MN ( у см), якщо об'єм піраміди дорівнює 152 см3, а площа її основи 57 см2.
Розв’язання:
-
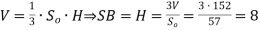
-
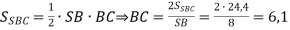
-
MN – середня лінія
 , тому
, тому 
Відповідь: 3,05
34.Знайдіть найменше значення параметра ![]() , при якому рівняння
, при якому рівняння ![]() має додатній корінь.
має додатній корінь.
Розв’язання:
-

-

- З пунктів 1) та 2) випливає, що рівняння має розв’язки тоді і тільки тоді, коли ліва частина набуває найменшого значення, а права найбільшого. Маємо систему:

 . Корінь за умовою завдання повинен бути додатнім. Найменший такий корінь (а відповідно і найменше значення параметра) маємо при
. Корінь за умовою завдання повинен бути додатнім. Найменший такий корінь (а відповідно і найменше значення параметра) маємо при ![]()
Відповідь: -2,625
Варіант 34 (ЗНО – 2014)
-
 33. Через точки А і В, що лежать на колах верхньої та нижньої основ циліндра і не належать одній твірній, проведено площину, паралельну осі циліндра. Відстань від центра нижньої основи до цієї площини дорівнює а = 2 см, а площа утвореного перерізу S = 60
33. Через точки А і В, що лежать на колах верхньої та нижньої основ циліндра і не належать одній твірній, проведено площину, паралельну осі циліндра. Відстань від центра нижньої основи до цієї площини дорівнює а = 2 см, а площа утвореного перерізу S = 60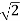 см2. Визначте довжину відрізка АВ (у см), якщо площа бічної поверхні циліндра дорівнює
см2. Визначте довжину відрізка АВ (у см), якщо площа бічної поверхні циліндра дорівнює  см2 (а = 2 см, S = 40
см2 (а = 2 см, S = 40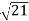 см2,
см2, 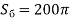 см2 , а =
см2 , а =  см, S = 54
см, S = 54 см2,
см2,  см2)
см2)
Розв’язання:
Нехай ![]() – радіус основи,
– радіус основи, ![]() висота циліндра.
висота циліндра.
1) ![]()
2) ![]()
3) ![]()
4) Прирівнюємо праві частини з рівностей 2) і 3).
![]()
-
З


|
|
І |
ІІ |
ІІІ |
|
|
10 |
25 |
100 |
|
|
10 |
20 |
9 |
|
|
2 |
|
|
|
|
24 + 300 = 324 |
84 + 400 = 484 |
360 + 81 = 441 |
|
|
18 |
22 |
21 |
Відповідь: 18 22 21
 34. Знайдіть усі від’ємні значення параметра а, при яких система
34. Знайдіть усі від’ємні значення параметра а, при яких система
![]()
![]()
![]()
![]() ає єдиний розв’язок. Якщо таке значення одне, то запишіть його у відповідь. Якщо таких значень декілька, то у відповідь запишіть їх суму.
ає єдиний розв’язок. Якщо таке значення одне, то запишіть його у відповідь. Якщо таких значень декілька, то у відповідь запишіть їх суму.
Розв’язання:
Перепишемо дану систему у вигляді: ![]()
Розглядаємо окремо перше рівняння:
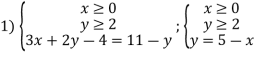
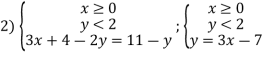


Друге рівняння запишемо у вигляді:
![]() - сукупність двох сімейств прямих.
- сукупність двох сімейств прямих.
Отримані множини зобразимо у прямокутній декартовій системі координат. Система має єдиний розв’язок, коли графіки мають єдину спільну точку.
1) ( -3 ; 2). Підставляємо координати цієї точки в рівняння функції ![]() , звідки
, звідки ![]()
2) ( 3 ; 2). Підставляємо координати цієї точки в рівняння функції ![]() звідки
звідки ![]() – не розв’язок.
– не розв’язок.
3) ( 0 ; -7). Підставляємо координати цієї точки в рівняння функції ![]() , звідки
, звідки ![]() – не розв’язок
– не розв’язок
4) ( 0 ; -7). Підставляємо координати цієї точки в рівняння функції ![]() звідки
звідки ![]() .
.
Сума від’ємних значень: -8,5 + (-3,5) = -12
Для другого варіанту зміниться лише друге рівняння. Воно буде мати вигляд:
![]() . Таким чином, для знаходження розв’язку підставимо координати точки: ( -3 ; 2) в рівняння
. Таким чином, для знаходження розв’язку підставимо координати точки: ( -3 ; 2) в рівняння ![]() , звідки
, звідки ![]() , та координати (0; -7) в рівняння
, та координати (0; -7) в рівняння ![]() , звідки
, звідки ![]() Сума від’ємних: -15
Сума від’ємних: -15
Відповідь: -12 -15
Варіант 35 (демонстраційний варіант 2015)
35. Два кола радіусів ![]() і
і ![]() дотикаються у точці K. До цих кіл проведено спільну дотичну MN (M – належіть більшому колу).
дотикаються у точці K. До цих кіл проведено спільну дотичну MN (M – належіть більшому колу).
1) Довести, що центри вказаних кіл та точка їхнього дотику лежать на одній прямій.
2) Знайти площу фігури, обмеженої відрізком MN та меншими дугами KN та KM.
Розв’язання:
 1) Нехай О1 – радіус кола з радіусом
1) Нехай О1 – радіус кола з радіусом ![]() , О – центр кола з радіусом
, О – центр кола з радіусом ![]() .
. ![]()
2) ![]() – трапеція
– трапеція
![]() ) . Проведемо
) . Проведемо ![]() .
. ![]() .
. ![]() .
.
З ![]()
Площа трапеції:
![]()
Знайдемо площі секторів ![]() та
та ![]() .
.
Нехай ![]() , тоді
, тоді ![]()
![]() . Площу сектора знаходимо за формулою:
. Площу сектора знаходимо за формулою: ![]() .
.
![]()
Шукана площа: ![]()
Відповідь: ![]()
36. Для всіх значень параметра ![]() розв’язати рівняння:
розв’язати рівняння:
![]()
Розв’язання:
Запишемо рівняння у вигляді: ![]() .
.
1) ![]() – корінь рівняння
– корінь рівняння
2) ![]() (*). Розглянемо геометричну інтерпритацію.
(*). Розглянемо геометричну інтерпритацію.
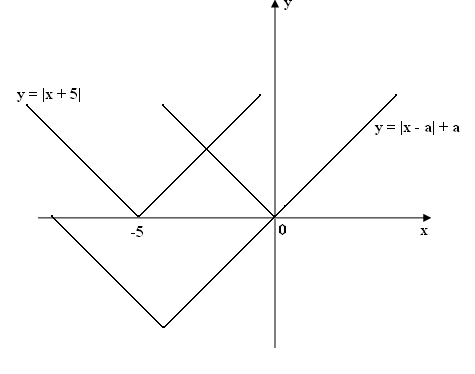
Якщо ![]() , то рівняння (*) має один корінь, який знаходимо з умови
, то рівняння (*) має один корінь, який знаходимо з умови ![]()
![]() . Враховуємо ОДЗ:
. Враховуємо ОДЗ: ![]() .
. ![]() .
.
Якщо ![]() , то розв’язком рівняння (*) будуть всі
, то розв’язком рівняння (*) будуть всі ![]() , але при цьому необхідно, щоб
, але при цьому необхідно, щоб ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
Варіант 36 (пробне ЗНО - 2015)
35. У трапеції ABCD (BC||AD) діагональ АС є бісектрисою гострого кута А. Ця діагональ перетинає середню лінію трапеції в точці Р.
-
Доведіть, що

-
 Обчисліть площу трапеції ABCD, якщо ВС = 5 см, AD = 13 см, площа трикутника АРВ дорівнює 5 см2
Обчисліть площу трапеції ABCD, якщо ВС = 5 см, AD = 13 см, площа трикутника АРВ дорівнює 5 см2
Розв’язання:
1) ![]() – бісектриса
– бісектриса ![]() , тому
, тому ![]() ;
; ![]() (як внутрішні різносторонні при паралельних прямих
(як внутрішні різносторонні при паралельних прямих ![]() та січній
та січній ![]() ). Таким чином,
). Таким чином, ![]() – рівнобедрений. Оскільки
– рівнобедрений. Оскільки ![]() (середня лінія), то
(середня лінія), то ![]() – медіана
– медіана ![]() , а отже і висота.
, а отже і висота. ![]() .
.
2) З вершини А проводимо ![]() . Відрізок
. Відрізок ![]() – висота трапеції ABCD, а також висота
– висота трапеції ABCD, а також висота ![]() .
.
![]() . З іншого боку:
. З іншого боку: ![]() .
.
![]()
Відповідь: 36 см2
36. Знайдіть усі значення параметра ![]() , за яких рівняння
, за яких рівняння ![]() має єдиний корінь.
має єдиний корінь.
Розв’язання:
Розглянемо праву частину рівняння.
![]() .
.
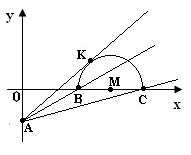 Використаємо геометричну інтерпритацію. Права частина – це півколо з центром в точці (9; 0) та радіусом 3. Ліва частина – це множина прямих, які проходять через точку А(0; -3) та змінюють свій кутовий коефіцієнт в залежності від значення параметра
Використаємо геометричну інтерпритацію. Права частина – це півколо з центром в точці (9; 0) та радіусом 3. Ліва частина – це множина прямих, які проходять через точку А(0; -3) та змінюють свій кутовий коефіцієнт в залежності від значення параметра ![]() .
.
Точка В(6; 0). ![]() . Точка С(12; 0).
. Точка С(12; 0). ![]() . Зауважимо, що при
. Зауважимо, що при![]() рівняння має два корені.
рівняння має два корені.
Розглянемо пряму АК (дотична до кола). В цьому випадку рівняння також має один корінь. Дане рівняння підносимо до квадрату: ![]() ;
;
![]() . Для того, щоб рівняння мало один корінь необхідно, щоб
. Для того, щоб рівняння мало один корінь необхідно, щоб ![]() .
. ![]() . При
. При ![]() маємо пряму
маємо пряму ![]() , яка очевидно не має точок перетину з півколом.
, яка очевидно не має точок перетину з півколом.
![]() :
: ![]()
Варіант 37 (ЗНО - 2015)
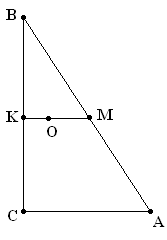 35. У прямокутному трикутнику АВС точка М є серединою гіпотенузи АВ, довжина якої дорівнює 26 см. Точка О віддалена від вершин В і С на 15 см, а від сторони ВС – на
35. У прямокутному трикутнику АВС точка М є серединою гіпотенузи АВ, довжина якої дорівнює 26 см. Точка О віддалена від вершин В і С на 15 см, а від сторони ВС – на ![]() см. З точки О на катет ВС опущено перпендикуляр ОК, точка К належить відрізку ОМ.
см. З точки О на катет ВС опущено перпендикуляр ОК, точка К належить відрізку ОМ.
- Доведіть, що чотирикутник КМАС – трапеція.
- Визначте площу трапеції КМАС.
Розв’язання:
1) За умовою ![]() , отже,
, отже, ![]() – рівнобедрений, тому висота
– рівнобедрений, тому висота ![]() є медіаною.
є медіаною. ![]() – середина
– середина ![]() ,
, ![]() – середина
– середина ![]() . Таким чином,
. Таким чином, ![]() середня лінія
середня лінія ![]() ,
, ![]() – трапеція.
– трапеція.
2) З ![]() . Точка М – середина АВ, тому ВМ =
. Точка М – середина АВ, тому ВМ = ![]() .
.
З ![]() (5, 12, 13 – піфагорова трійка)
(5, 12, 13 – піфагорова трійка)
![]()
![]() , тоді
, тоді
![]()
Відповідь: 90 см2
36. При яких значеннях параметра ![]() рівняння
рівняння ![]() на проміжку [0; 1] має рівно два різні корені?
на проміжку [0; 1] має рівно два різні корені?
Розв’язання:
Знаменник: ![]()
Розглянемо рівняння: ![]() . Корінь
. Корінь ![]() належить данному відрізку за умови
належить данному відрізку за умови ![]() ,
, ![]()
Квадратичне рівняння ![]() .
. ![]() .
.
![]()
Необхідно, щоб ![]() .
.
Обмеження: 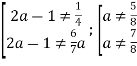
Відповідь: ![]()
Варіант 38 (пробне ЗНО - 2016)
31. Знайдіть найбільше та найменше значення функції ![]() на відрізку
на відрізку ![]() .
.
Розв’язання:
1) Знаходимо похідну: ![]()
2) Знаходимо критичні точки з умови ![]()
![]() . Єдина критична точка, що належить відрізку
. Єдина критична точка, що належить відрізку ![]() – це точка
– це точка ![]()
3) Знаходимо значення функції в знайденій критичній точці і на кінцях відрізка.
![]()
![]()
Відповідь: ![]()
32. У правильній чотирикутній піраміді SABCD з точки О, яка є основою висоти SO, до бічного ребра SA проведено перпендикуляр ОМ довжиною ![]() . Двогранний кут при бічному ребрі піраміди дорівнює 120°.
. Двогранний кут при бічному ребрі піраміди дорівнює 120°.
-
Доведіть, що пряма

- Знайдіть об'єм піраміди SABCD
Розв’язання:
 1) Нехай
1) Нехай ![]() .
.
![]() (як діагоналі квадрата), пряма
(як діагоналі квадрата), пряма ![]() містить проекцію
містить проекцію ![]() на основу
на основу ![]() . Тому
. Тому ![]() (за теоремою про три перпендикуляри).
(за теоремою про три перпендикуляри).
З ![]()
![]() .
.
З ![]() :
: ![]() ;
;
![]() .
.
З ![]() :
: ![]()
З ![]() (за теоремою косинусів):
(за теоремою косинусів):
![]() . Розглянемо чисельник:
. Розглянемо чисельник:
![]() ;
; ![]() .
.
![]() (ознака перпендикулярності прямої та площини)
(ознака перпендикулярності прямої та площини)
2) ![]() (лінійний кут двогранного кута).
(лінійний кут двогранного кута). ![]() – рівнобедрений, тому висота МО є бісектрисою.
– рівнобедрений, тому висота МО є бісектрисою.
З ![]()
З ![]() , тоді
, тоді ![]()
З ![]() :
: ![]()
![]()
Відповідь: 972
33. Розв’яжіть нерівність ![]() при всіх значеннях параметра
при всіх значеннях параметра ![]() .
.
Розв’язання:
ОДЗ: ![]()
1) ![]() (випливає безпосередньо з ОДЗ)
(випливає безпосередньо з ОДЗ)
2) ![]()
3) ![]() . Розглянемо функцію:
. Розглянемо функцію: ![]() .
.
![]() – критична точка. При переході через точку 0 похідна змінює знак з «+» на «-», отже,
– критична точка. При переході через точку 0 похідна змінює знак з «+» на «-», отже, ![]() – точка максимуму.
– точка максимуму.
![]()
 Розглянемо геометричну інтерпритацію.
Розглянемо геометричну інтерпритацію.
Побудуємо графік функції ![]() .
.
Далі, проводимо прямі ![]() .
.
а) ![]() . При
. При ![]()
б) ![]() . При
. При ![]()
в) ![]() . При
. При ![]() , де
, де ![]() – корені рівняння
– корені рівняння ![]() . Підносимо до квадрата.
. Підносимо до квадрата.
![]() . Останнє рівняння підносимо до квадрата.
. Останнє рівняння підносимо до квадрата. ![]()
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то
, то ![]()
Варіант 39 (ЗНО - 2016)
31. Побудуйте графік функції ![]() . Користуючись графіком, визначте область значень цієї функції.
. Користуючись графіком, визначте область значень цієї функції.
 Розв’язання:
Розв’язання:
![]()
![]()
32. Основою піраміди SABCD є ромб ABCD, більша діагональ якого АС = 30. Грань SBC є рівнобедреним трикутником (SB = SC) і перпендикулярна до площини основи піраміди. Ребро SC нахилено до площини основи піраміди під кутом 30°. Визначте кут між площинами (SAD) і (ADC), якщо висота піраміди дорівнює 5.
Розв’язання:
 За умовою (SBC)
За умовою (SBC) ![]() (ABC), тому висота SO рівнобедреного трикутника SBC є висотою піраміди.
(ABC), тому висота SO рівнобедреного трикутника SBC є висотою піраміди. ![]() .
.
Проведемо ![]() (за теоремою про три перпендикуляри, OK проекція похилої SK).
(за теоремою про три перпендикуляри, OK проекція похилої SK).
![]() - лінійний кут двогранного кута, тобто кут між площинами (SAD) і (ADC).
- лінійний кут двогранного кута, тобто кут між площинами (SAD) і (ADC).
З трикутника SOC: ![]() , тоді
, тоді ![]() .
.
Діагоналі ромба перпендикулярні і точкою перетину M діляться навпіл, тому з трикутника ВМС: ![]() .
.
Запишемо площу ромба: ![]() , звідки
, звідки ![]() .
.
З трикутника SOK: ![]()
Відповідь: ![]()
33. Розв’яжіть рівняння ![]() в залежності від значень параметра
в залежності від значень параметра ![]() .
.
Розв’язання:
1) ![]()
![]()
![]() ;
; ![]()
2) При ![]() рівняння не визначене, бо не існує
рівняння не визначене, бо не існує ![]() на множині дійсних чисел
на множині дійсних чисел
3) ![]()
4) ![]()
![]() ;
;
![]() ;
; ![]()
Відовідь: якшо ![]() , то рівняння не має змісту; якщо
, то рівняння не має змісту; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() ,то
,то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]()
Варіант 40 (пробне ЗНО – 2017)
31. Задано функцію ![]()
-
Розв’яжіть рівняння:

-
Спростіть вираз

-
Побудуйте графік функції

- Користуючись графіком, визначте область значень цієї функції.
Розв’язання:
1) ![]()
2) ![]()
 3)
3)
4) ![]()
32. Основою піраміди SABCD є паралелограм ABCD з гострим кутом А. Ребро SB перпендикулярне до прямих АВ і ВС. Проекцією ребра SD на площину основи є відрізок довжини 10 см, який утворює зі стороною AD кут 30°. Визначте кут між площинами (SAD) і (АВС), якщо SD = 15 см.
Розв’язання:
 Проведемо
Проведемо ![]() – проекція
– проекція ![]() на площину (АВС). За теоремою про три перпендикуляри,
на площину (АВС). За теоремою про три перпендикуляри, ![]() . SKB = φ – шуканий (лінійний кут двогранного кута).
. SKB = φ – шуканий (лінійний кут двогранного кута).
![]()
![]() (катет лежить проти кута 30°)
(катет лежить проти кута 30°)
![]()
Відповідь: ![]()
33. Розв’яжіть рівняння ![]() залежно від значень параметра
залежно від значень параметра ![]() .
.
Розв’язання:
ОДЗ: 
![]()
![]()
![]()
![]()

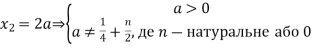
Відповідь: якщо ![]() , то
, то ![]() ;
;
якщо ![]() то
то ![]() ;
;
якщо ![]() , то
, то ![]()
Варіант 41 (ЗНО – 2017)
31. Задано функцію ![]() .
.
-
Визначте координати точок перетину графіка функції
 з осями координат.
з осями координат.
-
Побудуйте графік функції
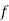 .
.
-
Запишіть загальний вигляд первісних для функції
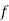 .
.
-
Обчисліть площу фігури. Обмеженої графіком функції
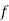 та осями
та осями  і
і 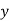 .
.
 Розв’язання:
Розв’язання:
1) ![]()
![]()
Відповідь: перетин з віссю абсцис: (3 ; 0) , перетин з віссю ординат: (0 ; 9).
2)
3) Відповідь: ![]()
4) 
Відповідь: 9
32. Основою правильної призми АВСА1В1С1 є рівносторонній трикутник АВС. Точка К – середина ребра ВС. Площина, що проходить через точки А, К та В1 , утворює з площиною основи призми кут α . Визначте об’єм призми АВСА1В1С1 , якщо відстань від вершини А до грані ВВ1С1С дорівнює ![]() .
.
 Розв’язання:
Розв’язання:
![]() – проекція похилої
– проекція похилої ![]() ,
, ![]() (за теоремою про три перпендикуляри)
(за теоремою про три перпендикуляри)
![]() (лінійний кут двогранного кута)
(лінійний кут двогранного кута)
Відстань від А до грані ВВ1С1С – довжина відрізка АК.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Відповідь: ![]()
33. Розв’яжіть систему рівнянь ![]() залежно від значень параметра
залежно від значень параметра ![]() .
.
Розв’язання:
![]()
1) ![]() , але з другого рівняння
, але з другого рівняння ![]() . Розв’язків немає.
. Розв’язків немає.
2) ![]() . З другого рівняння:
. З другого рівняння: ![]()
![]() ;
;
![]() ;
;
![]()
Необхідно: 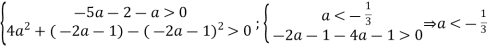
![]()
Необхідно: ![]()
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]()
Варіант 43 (ЗНО – 2018)
 31. Задано функції
31. Задано функції ![]() і
і ![]()
-
Побудуйте графік функції

-
Побудуйте графік функції

-
Визначте абсциси точок перетину графіків функцій
 і
і 
-
Обчисліть площу фігури, обмеженої графіками функцій
 і
і 
Розв’язання:
3) 
![]() ;
; ![]()
Значення ![]()
![]() . Від’ємних коренів немає.
. Від’ємних коренів немає.
4) 
![]()
 32. У правильній чотирикутній піраміді SABCD сторона основи ABCD дорівнює с, а бічне ребро SA утворює з площиною основи кут α. Через основу висоти піраміди паралельно грані ASD проведено площину β.
32. У правильній чотирикутній піраміді SABCD сторона основи ABCD дорівнює с, а бічне ребро SA утворює з площиною основи кут α. Через основу висоти піраміди паралельно грані ASD проведено площину β.
- Побудуйте переріз піраміди SABCD площиною β.
- Обгрунтуйте вид перерізу.
- Визначте периметр перерізу.
Розв’язання:
1) Нехай точка О – основа висоти піраміди (точка перетину діагоналей квадрата ABCD, що є основою піраміди). Через точку О проводимо EF || AB. PE та PF – апофеми (висоти бічних граней) піраміди. В площині (PEF) через точку О проводимо OT || PE ( T Є PF). В площині (PBC) через точку T проводимо NM || BC. В площині (АВС) через точку О проводимо KL || BC. Чотирикутник KLMN – шуканий переріз.
2) NM || BC, KL || BC ![]() NM || KL, отже, KLMN – трапеція. NK – середня лінія
NM || KL, отже, KLMN – трапеція. NK – середня лінія ![]() , ML – середня лінія
, ML – середня лінія ![]() .
.
![]()
KLMN – рівнобічна трапеція.
3) ![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
33. Розв’язати нерівність: ![]()
Розв’язання:
ОДЗ: ![]()
Розглянемо тричлен ![]()
![]() ;
; ![]()
На ОДЗ: ![]()
1) ![]() . Розв’язок даної нерівності отримаємо із графічного зображення. Розв’язком будуть ті множини додатних
. Розв’язок даної нерівності отримаємо із графічного зображення. Розв’язком будуть ті множини додатних ![]() , де графіки функцій лежать по різні боки від осі абсцис.
, де графіки функцій лежать по різні боки від осі абсцис. ![]() – розв’язок для всіх допустимих значень параметра.
– розв’язок для всіх допустимих значень параметра.
2) ![]() .
.
3) ![]()
 Відповідь: якщо
Відповідь: якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то
, то ![]()
1


про публікацію авторської розробки
Додати розробку

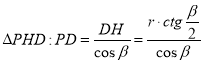
-

Рязанова Галина Яківна
26.04.2023 в 15:08
Дякую, дуже корисно!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kosyhina Elena
12.12.2022 в 17:13
Дякую!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

ковальчук олена
28.04.2020 в 07:21
Дякую, дуже корисно
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Valery
21.04.2020 в 17:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вєлікоцька Ірина Іванівна
13.02.2020 в 08:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сергієнко Алла Іванівна
26.01.2020 в 19:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бережецька Людмила Сергіївна
22.01.2020 в 17:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Степанова Оксана
31.07.2019 в 09:01
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жолобанюк Оксана Дмитрівна
12.05.2019 в 19:41
СПАСИБІ
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків