Розв'язування ірраціональних рівнянь

Про матеріал

Методичні рекомендації до проведення уроку по темі «Розв’язування ірраціональних рівнянь різними методами»

Перегляд файлу

fon makarenko_logo Міністерство освіти і науки України

Київський професійно-педагогічний коледж імені Антона Макаренка

Методичні рекомендації до проведення уроку по темі «Розв’язування ірраціональних рівнянь різними методами»

для студентів І курсу

денної форми навчання

Дисципліна: «Математика»

Спеціальність: 081 «Право»

Київ 2019

Укладач: викладач Київського професійно-педагогічного коледжу імені Антона Макаренка, спеціаліст вищої категорії Л. М .Мартиненко.

Розглянуто і схвалено на засіданні циклової комісії загальнонаукових дисциплін.

Протокол № __________ від « _____» ________________ 201_____ р.

Голова комісії :______________ О. В. Щепіло

Зміст

Вступ…………………………………………………………………………..4

Основна частина……………………………………………………….6

Висновок ……………………………………………………………………………………………………15

Список використаних джерел……………………………………………………………………16

Додатки ……………………………………………………………………………………………….…17

ВСТУП

Учитель готується до хорошого уроку все життя... Така духовна і філософська основа нашої професії і технологія нашої праці: щоб дати учням іскорку знань, вчителеві треба ввібрати ціле море світла

В. Сухомлинський

Життя змінюється дуже швидко. Напевно, одна з професій, фахівці якої мають змінюватись одночасно з нею, – це професія вчителя. Адже кожне покоління має справу з новими досягненнями, проблемами та турботами. І першими, хто вказує стежку в іноді не зрозумілому, а підчас і ворожому для учня світі, є звичайні вчителі.

Сучасний урок не може бути створений за шаблоном, оскільки це завжди живий, динамічний процес. І тому сьогодні особливими вимогами до вчителя-професіонала стають не тільки глибокі знання, сформовані педагогічні вміння та навички, високий рівень культури, розвинені особистісні якості, а й бажання працювати в атмосфері творчості. Математика має широкі можливості для інтелектуального розвитку особистості, вона є засобом вивчення фізики, хімії, інформатики, астрономії, біології, загальнотехнічних і спеціальних дисциплін, вона також є мовою техніки, а розвинене логічне мислення сприяє засвоєнню гуманітарних предметів.

Разом з тим активізація пізнавальної діяльності учнів під час вивчення математики є однією з проблем сучасної освіти. Це пов'язане, в першу чергу, із зниженням інтересу молоді до навчання в цілому. XXI століття – час переходу до високотехнологічного інформаційного суспільства, в якому якість людського потенціалу, рівень освіченості й культури всього населення набувають вирішального значення. Урізноманітнення форм проведення уроку, цілеспрямоване використання мультимедійних засобів зацікавлює учнів, активізує їхню здатність сприймати новий матеріал, розвиває в них творчий потенціал.

Будувати кожен урок так, щоб у всіх учнів був стійкий інтерес, навчальна активність і бажання творити й пізнавати, експериментувати, формулювати й перевіряти гіпотези – завдання сучасного вчителя. Без застосування ефективних педагогічних ідей, інноваційних методів та комп’ютерних технологій при підготовці таких уроків тут не обійтися.

Сучасний урок- це урок демократичного спрямування. Вчитель проводить його не так для учнів, як разом з ними, навчає не тільки словом, а й організованою справою. Традиційними вимогами до сучасного уроку є те, що на заняттях учні повинні наводити приклади із життя, робити порівняння, висновки, працювати з підручником, здійснювати експеремент, заносити дані до таблиць, виконувати вимірювання та розрахунки, висувати гіпотези, звертатись до свого практичного досвіду.

Для сучасного уроку характерними ознаками є:

варіативність і гнучкість уроку;
спрямованість уроку на особливість учня;
повне засвоєння матеріалу на уроці;
оптимізація форм роботи на уроц;
системний підхід до архітектури уроку та процесу навчання.

Основна частина

Урок «Розв’язування ірраціональних рівнянь різними методами»

Тривалість уроку: 80 хв.

Тип уроку: закріплення знань і умінь вивченого матеріалу

Вид уроку: урок-практикум

Технологія уроку: ІКТ, проектне навчання, розвиваюче навчання

Мета:

Навчальна:

узагальнити і систематизувати знання, здобуті учнями в процесі розв’язування ірраціональних рівнянь;
провести корекцію знань і вмінь учнів.

Розвиваюча:

розвивати способи і прийоми мислення, індивідуальні здібності учнів, їх пізнавальні інтереси;
навички колективної та групової роботи;
уміння використовувати сформовані знання, навички й уміння в нових ситуаціях.

Виховна:

виховувати розумову культуру;
культуру усного та писемного мовлення та міжособистісного спілкування;
працьовитість, старанність, охайність ведення записів;
уміння об’єктивно оцінювати свої результати та результати інших.

Формувати компетентності:

загальнокультурну (застосовувати методи самовиховання, орієнтовані на загальнолюдські цінності);
здоров’язбережувальну (здатність учня дбайливо ставитися до власного здоров’я та здоров’я інших людей);
інформаційно-комунікаційн (здатність учня використовувати інформаційно-комунікаційні технології та відповідні засоби для виконання завдань);
ключову (певний рівень знань, умінь, навичок, ставлень, які можна застосувати при розв’язувані ірраціональних рівнянь);
комунікативну(здатність учня застосовувати у конкретному виді спілкування знання математичної мови, способи взаємодії з людьми, що оточують її та перебувають на відстані, навички роботи у групі, володіння різними ролями);
предметну (галузеву) (сукупність знань, умінь необхідних для виконання учнями певних дій з метою розв’язання навчальних проблем, задач, ситуацій);
проектно-технологічну (здатність учнів застосовувати знання, уміння та особистий досвід у предметно-перетворювальній діяльності);
соціальну (здатність учня продуктивно співпрацювати з партнерами у групі та команді, виконувати різні ролі та функції у колективі).

Обладнання: дошка, роздатковий матеріал для учнів, мультимедійні засоби, презентація.

Хід уроку:

І. Організаційний етап. Повідомлення теми і мети уроку. (5 хв.)

Учні записують у зошит дату й тему уроку. (заздалегідь написано на дошці)

Учитель повідомляє мету уроку.

Систематизація і узагальнення вивчених методів розв’язування ірраціональних рівнянь.

Розвиваємо: логічне мислення; пам’ять; пізнавальний інтерес до математики та інформатики; навички самооцінки і самоконтролю.

Виховуємо: працьовитість; етику та культуру спілкування; навички взаємопідтримки та взаємодопомоги.

У кожного з вас на столі лист оцінки діяльності, в який ви повинні виставляти кількість набраних балів за кожний вид роботи. В кінці уроку ми підведемо підсумок, перевівши загальну кількість балів в оцінку, користуючись шкалою. Бажаю всім успіху!

ІІ. Актуалізація опорних знань. (15 хв.)

Історична довідка(слайди)

Поняття ірраціональності асоціюється завжди із зображенням кореня. Знак кореня з’явився у 1525 році. До нашого часу зображення змінювалось. Хто ж вперше ввів це зображення?

Давньогрецький учений-дослідник, який вперше довів існування ірраціональних чисел

1.Що необхідно виконати для отриманих значень змінної при розв'язуванні ірраціональних рівнянь? Перевірку.

2.Спосіб, яким проводиться перевірка розв'язків ірраціональних рівнянь? Підстановка.

3.Як називається знак кореня? Радикал.

4.Як називаються рівняння, в яких під знаком кореня міститься змінна? Ірраціональні.

5.Як називається корінь третього степеня? Кубічний.

6.Скільки коренів має рівняння х²=а, якщо а <0? Жодного.

Евклід – великий вчений, який жив у ІІІ столітті до нашої ери в Стародавній Греції. Був запрошений в Олександрію царем Птоломеєм І для організації математичної школи. Евклід відомий усьому світові завдяки своїй праці «Начала», яка складається з 13 книг, до яких пізніше додали 14 та 15 книги.

За «Началами» Евкліда протягом багатьох століть вивчали геометрію в усіх школах.

Хто вперше ввів зображення кореня?

1.Скільки розв'язків має рівняння х²=0? Один.

2.Корінь якого степеня існує з будь-якого числа? Непарного.

3.Як називається корінь другого степеня? Квадратний.

4.Скільки коренів має рівняння х²=а, якщо а >0? Два.

5.Корінь якого степеня існує лише з невід'ємного числа? Парного.

6.Як називається корінь рівняння, який утворюється в результаті нерівносильних перетворень? Сторонній.

Декарт – великий французький філософ, математик, який першим дослідив важливі властивості алгебраїчних рівнянь, першим ввів поняття змінної величини, один із засновників аналітичної геометрії.

Головні роботи: «Геометрія», «Роздуми про метод».

3.Хто ввів сучасне зображення кореня?

1.1.Як називається рівність в якій міститься змінна? Рівняння.

2.Як називається значення змінної, при якому рівняння перетворюється на вірну числову рівність? Корінь.

3.”Мовчазний” вчитель сучасного учня? Комп’ютер.

4.Яку теорему використовують при розв'язуванні квадратних рівнянь? Вієта.

5.Як називаються рівняння, якщо вони мають одні й ті самі корені або не мають корені взагалі? Рівносильні.

6.Як називаються ірраціональні вирази, що містять протилежні арифметичні дії “-” та “+”? Спряжені.

Ньютон – великий англійський вчений, який відкрив основні закони природи. Ньютон ввів сучасне зображення кореня. Засновник класичної механіки, законів всесвітнього тяжіння. За видатні заслуги його було названо «прикрасою людського роду».

Розумова розминка.

Переходимо до бліц-опитування (за правильну відповідь – 1 бал).

Завдання 1. Увага на екран. Знайдіть, будь-ласка, серед запропонованих рівнянь ірраціональні (слайд):

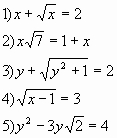
Відповідь:1,3,4.

Завдання 2. Чи являється число коренем рівняння:

1) ,

2) ,

Завдання 3. Знайдіть корені рівняння:

1) (216).

2) (0).

3) (-710).

4) (5; -).

IІІ. Узагальнення та систематизація знань. ( 40 хв.)

1. Тестування (10хв.)

Для перевірки готовності до уроку пропоную пройти тестування (за кожну правильну відповідь – 1 бал).

2. Фронтальна робота (30 хв.)

Повторення вивчених методів розв’язування ірраціональних рівнянь. Учні за бажанням виходять до дошки і розв’язують ірраціональні рівняння, коментуючи розв’язок. Всі працюють на місцях.

Метод піднесення обох частин рівняння до одного степеня

Якщо обидві частини рівняння піднести до непарного степеня, то отримаємо рівняння, рівносильне даному.

При піднесенні обох частин рівняння до парного степеня отримаємо рівняння, яке є наслідком даного.

Приклад 1. Розв'язати рівняння = 2 – х .

Розв'язання:

= (2 – х)²;

х – 2 = 4 – 4х + х²;

х² – 5х + 6 = 0;

х = 2 або х = 3.

Перевірка: 1) = 2 – 2; 2) ≠ 2 – 3.

Відповідь: 2.

Приклад 2. Розв’язати рівняння .

Розв’язання:тобто

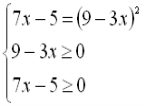
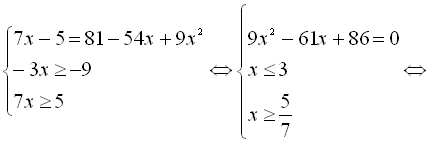
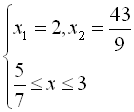З даної системи випливає, що лише 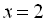є коренем початкового рівняння.

Відповідь: 2.

Додатково. Розв’язати рівняння:

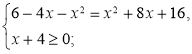
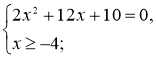
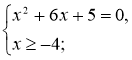
Розв’язання:

Х₁=-1; х₂=-5, сторонній корінь

Відповідь: -1

Метод заміни змінних

Даний метод зручно застосовувати тоді, коли при піднесенні обох частин рівняння до одного і того самого степеня виникають громіздкі перетворення.

Приклад 3. Розв’язати рівняння: .

Розв’язання.

Нехай , , тоді .

Маємо рівняння .

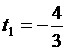
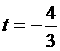сторонній корінь, так як не задовольняє умову .

Використаємо заміну:,

Відповідь:.

Приклад 4. Розв’язати рівняння .

Додатково. Розв’язати рівняння: .

Метод розкладання на множники

Метод розкладання на множники полягає в розкладанні всіх доданків рівняння на множники, прирівнявши їх до нуля. Потім, знайшовши ОДЗ розв’язати сукупність множників як окремого рівняння. Відкинути сторонні корені.

Приклад 5. Розв’язати рівняння:

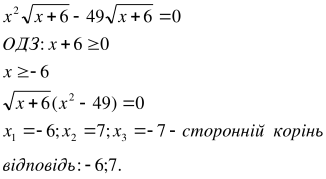
Приклад 6. Розв’язати рівняння .

Метод використання властивостей функції (Метод «Пильного погляду»). Застосовують для розв’язання рівнянь виду . Якщо функція, що стоїть в лівій частинні монотонна то таке рівняння має не більше одного кореня. Потім методом підбору, з урахуванням ОДЗ знаходять цей корінь, або показують що його не існує.

Приклад 7. Розв’язати рівняння:

Приклад 8. Розв’язати рівняння:

Графічний метод

Графічний метод базується на побудові графіків відповідних функцій, які стоять в обох частинах рівняння, та знаходженні їхніх точок перетину, що є відповідно розв’язками даного рівняння. Недоліком даного методу, є те, що для більшості функцій ми не зможемо знайти точного розв’язку.

Приклад 9. Розв’язати рівняння: .

Приклад 10. Розв’язати рівняння

IV. Перевірка засвоєння знань і вмінь учнів. (15 хв.)

Самостійна робота.

Взаємоперевіркою учні підраховують кількість набраних балів .

V. Підведення підсумків уроку. (5 хв.)

На уроці ми вивчили що таке ірраціональні рівняння та з’ясували, які рівняння є рівносильними. Познайомились з методами розв’язування ірраціональних рівнянь. Систематизували знання правил утворення рівносильних рівнянь, з'ясували випадки, коли необхідно обов'язково перевіряти одержані розв'язки підстановкою їх в дане рівняння. Розглянули приклади розв'язування найпростіших ірраціональних рівнянь. Набули навичок і вмінь розв’язувати ірраціональні рівняння.

Запитання: (метод незакінчених речень )

1) Ірраціональним рівнянням називається…..(рівняння, що містить змінну під знаком кореня або змінна із дробовим показником. ).

2) Розв’язати рівняння означає …….(знайти усі його корені або довести, що їх немає).

3) Основними методами розв’язування ірраціональних рівнянь є ……(через ОДЗ, піднесення обох частин рівняння до одного й того ж самого степеня; заміна змінної, графічний і т. д.)

4) При піднесенні обох частин рівняння до непарного степеня завжди отримуємо ……(рівняння, рівносильне даному).

5) При піднесенні обох частин рівняння до парного степеня завжди отримуємо

……(рівняння – наслідок).

Висновок

Математика – одна з найдавніших наук. Математика та її методи мають неоціянене значення для прогресу науки і практичної діяльності. У зв’язку з цим перед математикою виникають нові завдання, які дають можливість глибше й докладніше вивчати явища оточуючого нас світу і розв’язувати практичні задачі.

Математика перетворилась в необхідне знаряддя пізнавання, без якого неможливий розвиток знань.

Без сучасної математики з її розвинутим логічним і обчислювальним апаратом був би неможливий розвиток інших наук, інженерної справи, організації виробництва. Залишилися б нерозв’язаними численні проблеми авіації та космонавтики, метереології і радіотехніки.

Список використаних джерел

Бевз Г.П., Бевз В.Г. Математика. Рівень стандарту, 10 клас: Підруч. для загальноосвітніх навчальних закладів – К.:Генеза, 2012.
Возняк Г., Підручна М., Моховик О. Математика. Контроль навчальних досягнень. Збірник завдань. 10 клас. Рівень стандарту. – Тернопіль: Підручники і посібники, 2011.
Бевз В.Г. Історія математики. – Х.: «Основа», 2006. 16. Енциклопедія для дітей. Математика . Ред. Колегія : Аксьонова М., Володін В. – К., Школа, 2007.
Возняк Г., Возняк О., Бабій Н. Математика. 10 клас. Збірник тестових завдань. Рівень стандарту. – Тернопіль: Підручники і посібники, 2010.
Збірник завдань для державної підсумкової атестації з математики. 11 клас. У 2 книгах. За ред. Бурда М., Біляніна О., Вашуленко О, Прокопенко Н.. – Х.: Гімназія, 2008.
Мерзляк А., Полонський В., Рабінович Ю., Якір М. Збірник задач і завдань для тематичного оцінювання з алгебри і початків аналізу для 10 класу. - Х.: Гімназія, 2005.
Мерзляк А., Полонський В., Рабінович Ю., Якір М. Збірник задач і завдань для тематичного оцінювання з геометрії для 10 класу. - Х.: Гімназія, 2003.
https://web.posibnyky.vntu.edu.ua/fmib/7mihalevich_elementarna_matematika_algebra_ch2/7.htm
https://naurok.com.ua/library/prezentacia-rozvazuvanna-irracionalnih-rivnan-60321.html