Розв’язування квадратних нерівностей. Алгебра 9 клас

Алгебра, 9 клас

Тема уроку: «Розв’язування квадратних нерівностей»

 

Мета:

• удосконалити вміння учнів розв’язувати квадратні нерівності за допомогою графічного способу і методу інтервалів; сформувати вміння знаходити область визначення функції, підготувати до самостійної роботи;
• повторити властивості квадратичної функції;
• розвиток обчислювальних навичок.

 

Ніколи не втрачай терпіння – це останній ключ, що відкриває двері.

Антуан А. де Сент- Екзюпері

Хід уроку.

 

І. Перевірка домашнього завдання.

До дошки йдуть два учні №497(б), №496 (а).

На місці працює учень з карткою, інший № 494 (в).

 

№497(б)

(х-2)(х+2) + х(х+7) ≤ 0

2х²+7х-4≤0

х₁ = -4   х₂ =0,5

 

 

 

-4           0,5      х

хє[-4;0,5]

 

№496 (а)

а) ≥0, х ≠ -7

(х+5)(х+7) ≥ 0,

+     -             +

-7            -5          х

х є (-∞; -7)[-5;+ ∞)

 

№ 494 (в)

 

›0,

(х-4)(2х+5)‹0,

х₁ = 4   х₂ = -2,5

+       -          +

-2,5         4           х

Запитання:

1. Від чого залежить розташування графіка квадратичної функції в координатній площині? ( D і а)
2. Коли графік квадратичної функції дотикається осі  абсцис? (D = 0)
3.  Коли графік квадратичної функції перетинає вісь   абсцис? (D › 0)

Розв’язати нерівності:

1. 2х² ›0 (R)
2. -8 х² ‹0 (R)
3. -3 х² › 0 ( Ø)
4. 6х²  ≤ 0 (0)

 

 

ІІ. Повторення (актуалізація)

Для того, щоб перейти до розв’язування нерівностей потрібно дещо повторити.

Квадрат. Під цифрами 1-9 квадрата розміщені питання, на які в тестовій формі дано 4 відповіді, серед яких тільки одна правильна. Учні самі обирають питання.

 

 

 

 

 

            

              

 

 

 

 

 

 

 

 

               

 

 

 

 

                    

 

 

 

 

 

 

 

 

               

 

 

 

                 

 

 

 

 

 

 

 

 

                

 

 

 

               

 

 

 

 

 

 

 

 

               

 

              

 

 

 

 

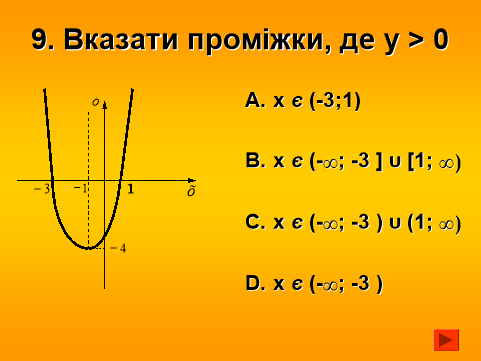
ІV. Розв’язування вправ

 

1. Розв’язати нерівність та вказати кількість цілих розв’язків, що розташовані на закритих проміжках.

(х³-25х)(9-х²) ≤0,

х(х-5)(х+5)(3-х)(3+х) ≤ 0,

х(х-5)(х+5)(х-3)(х+3) ≥ 0,

у = х(х-5)(х+5)(х-3)(х+3)

у=0, х=0, х=5, х=-5, х=3, х=-3

 

    -          +         -      +      -         +

          -5        -3     0     3       5           х

3+4 = 7

Відповідь: 7

 

2.  Знайти область визначення функції.

 у =

ОДЗ: х ² + 4х + 4 › 0,

(х+2)²  › 0,

у = (х+2)² 

у=0   (х+2)²  = 0,                                                                                             х

          х  = - 2                                                           -2

 

 

Відповідь: (-∞; -2)(-2;+ ∞)

 

3. Для учнів, які дома виконували додаткові завдання працюють з окремим завданням.

 

        Розв’язати нерівність і знайти суму цілих розв’язків.

 

≤0,

                                                               +      -            +           -           +

≤0,                                       -1        0             2          4                х

≤ 0,

х(х-2)(х-4)(х+1) ≤ 0,

у = 0    х(х-2)(х-4)(х+1 = 0,

            х=0, х=2, х=4, х=-1

 

-1+0+3+4 = 6

Відповідь: 6.

 

4. Розв’язати  нерівність.

(х² +5х – 6)(2х² + х – 3) ‹ 0,

2(х+6)(х-1)² (х+1,5) ‹ 0,                     +             -                  +             +

 х = -6, х = 1, х = 1,5                                -6                -1,5              1            х

 

• указати розв’язки нерівності,
• цілі розв’язки;
• знайти кількість цілих розв’язків

 

  Відповідь: х є (-6; - 1,5); -5,-4,-3,-2; 4.

 

Усна вправа на повторення.

 

Функція у = х² - 6х + 8.

Описати властивості функції.

На дошці є алгоритм описання властивостей функції.

 

 

              

 

 

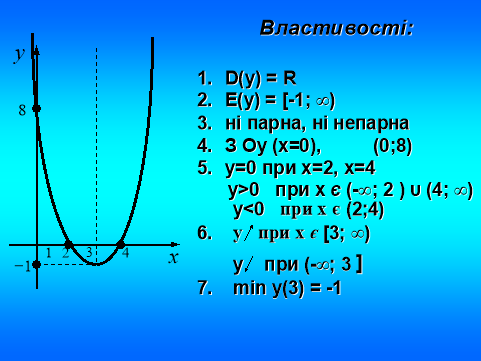
5.  № 501 (а)

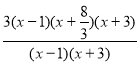≤ 0,

≤ 0,

у = (х-1)² (х+)(х+3),                               +          -              +               +

у=0       х-1)² (х+)(х+3) = 0,                        -3                        1                 х

              х = 1, х = -, х = -3

Відповідь: х є (-3; ].

 

V. Домашнє завдання.