"Розв’язування лінійних нерівностей з однією змінною. Числові проміжки" з математики в 9-му класі
Навчальний предмет. Алгебра .9 клас.
Розділ. Нерівності.
Ільніцька Людмила Василівна, вчитель математики, ЗОШ №11 м. Білої Церкви.
Тема уроку. Розв’язування лінійних нерівностей з однією змінною. Числові проміжки.
Мета уроку: Вивчити правила для застосування розв’язування нерівностей. Числові проміжки .
Формувати вміння та навички застосовувати ці правила під час розв’язування нерівностей.
Самостійно застосовувати набуті знання в стандартних і нестандартних ситуаціях, а також вміти систематизувати певні математичні твердження і робити висновки.
Епіграф: «Люди, не знайомі з алгеброю, не можуть уявити собі тих дивних речей, яких можна досягти за допомогою названої науки»
Г. Лейбніц.
Обладнання: мультимедійний проектор, презентація «Розв’язування лінійних нерівностей з однією змінною. Числові проміжки.»
Хід уроку
1.Перевірка домашнього завдання.
Поміняємося зошитами і перевіримо домашнє завдання. Якщо не має питань, то переходимо до наступного етапу нашого уроку.
№106. Розв’язати рівняння:
-
9
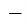 7х
7х  21 = 5
21 = 5  6х.
6х. 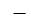 7х + 6х =
7х + 6х =  9 + 21 + 5;
9 + 21 + 5; 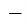 х = 17; х =
х = 17; х = 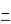 17.
17.
2)![]()
7 (х +3) ![]() 2 (х
2 (х ![]() 4) = 14; 7х + 21
4) = 14; 7х + 21 ![]() 2х + 8 = 14; 5х =
2х + 8 = 14; 5х = ![]() 21
21![]() 8
8 ![]() 14; 5х =
14; 5х = ![]() 15;
15;
х = ![]() 3.
3.
3) ![]() (
(![]() = 15.
= 15.
![]() + 14x + 49
+ 14x + 49 ![]() + 4x
+ 4x![]() 4 = 15; 18 х = 30;
4 = 15; 18 х = 30;
![]()
4) 5х![]() 2 = 3 (3х
2 = 3 (3х ![]() 1)
1)![]() 4х
4х ![]() 4.
4.
5х![]() 2 = 9х
2 = 9х ![]() 3
3 ![]() 4х
4х ![]() 4; 5х
4; 5х![]() 9х + 4х = 2
9х + 4х = 2![]() 3
3 ![]() 4; 0 = 5.
4; 0 = 5.
Відповідь: коренів немає.
5) 6х + (х ![]() 2) (х
2) (х ![]() 2) = (х +3)2
2) = (х +3)2![]() 6х +
6х +![]() +6х +9
+6х +9 ![]() 13; 0 = 0; Розв’зком є усі дійсні числа.
13; 0 = 0; Розв’зком є усі дійсні числа.
6) (х + 6) (х ![]() 1)
1) ![]() (х + 3) (х
(х + 3) (х ![]() 4) = 5х.
4) = 5х.
![]() x + 6x
x + 6x![]() 6
6 ![]()
![]() 6x
6x![]() 5
5![]() 12; х =
12; х = ![]() 6.
6.
2. Відтворення та узагальнення понять та засвоєння відповідної їм системи знань.
Математична розминка.
1.Сформулювати теорему про почленне додавання нерівностей.
Відповідь. Якщо а![]() і с
і с ![]() d,то а
d,то а![]()
![]()
![]() + d.
+ d.
2. Пояснити, які нерівності називають нерівностями однакового знака, а які нерівностями протилежних знаків.
Відповідь. Нерівність а![]() і с
і с ![]() d ( або а
d ( або а![]() і с
і с ![]() d ) називають нерівностями однакового знака, а нерівність а
d ) називають нерівностями однакового знака, а нерівність а![]() і с
і с ![]() d (або а
d (або а![]() с
с ![]() d)
d) ![]() нерівності протилежних знаків.
нерівності протилежних знаків.
3. Що є результатом почленного додавання нерівностей однакового знака?
Відповідь. Означає, що при почленному додаванні правильних нерівностей однакового знака результатом є правильна нерівність того самого знаку.
4. Сформулюйте теорему про почленне множення нерівностей.
Відповідь. Якщо а![]() , с
, с ![]() d і а
d і а![]() , с
, с ![]() d
d ![]() додатні числа, то а
додатні числа, то а![]() d.
d.
Аналогічно: якщо а ![]() і с
і с ![]() d і
d і![]() , с
, с ![]() d
d ![]() додатні числа, то
додатні числа, то ![]() с
с ![]() .
.
5. Що є результатом почленного множення нерівностей однакового знака?
Відповідь. При почленному множенні правильних нерівностей однакового знака, у яких ліві та праві частини![]() додатні числа, результатом є правильна нерівність того самого знака.
додатні числа, результатом є правильна нерівність того самого знака.
6. Сформулювати наслідок з теореми про почленне множення нерівностей.
Відповідь. Якщо а![]() і
і ![]()
![]() додатні числа, то
додатні числа, то ![]() , де
, де ![]() натуральне число.
натуральне число.
7. Що називають розв’язком нерівності з однією змінною?
Відповідь.Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює її в правильну числову нерівність.
8. Що означає розв’язати нерівність?
Відповідь. Розв’язати нерівність означає знайти всі її розв’язки або довести, що
розв’язків немає.
9. Що утворюють усі розв’язки нерівності?
Відповідь. Усі розв’язки нерівності утворюють множину розв’язків нерівностей.
10. Коли множиною розв’язків нерівності є порожня множина?
Відповідь. Якщо нерівність розв’язків не має,то кажуть, що множиною її розв’язків є порожня множина.
11. Які нерівності називають рівносильними?
Відповідь. Нерівності називають рівносильними, якщо вони мають одну й ту саму множину розв’язків.
3. Первинне сприймання нового матеріалу.
Властивості числових рівностей допомагали нам розв’язувати рівняння.
Аналогічно властивості числових нерівностей допоможуть розв’язати нерівності.
Розв’язуючи рівняння, ми замінили його іншим, більш простим рівнянням, але рівносильним даному. За аналогічною схемою розв’язують і нерівності.
При заміні рівняння на йому рівносильне використовують теореми про перенесення доданків з однієї частини рівняння в другу і про множення обох частин рівняння на одне те саме відмінне від нуля число.
Аналогічні правила застосовують і під час розв’язування нерівностей.
-
Якщо який
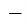 небудь доданок перенести з однієї частини нерівності в іншу, змінивши при цьому його знак на протилежний, то отримуємо нерівність, рівносильну даній.
небудь доданок перенести з однієї частини нерівності в іншу, змінивши при цьому його знак на протилежний, то отримуємо нерівність, рівносильну даній.
- Якщо обидві частини нерівності помножити (поділити) на одне й те саме додатне число, то отримуємо нерівність, рівносильну даній.
- Якщо обидві частини нерівності помножити (поділити) на одне й те саме від’ємне число, змінивши при цьому знак нерівностей на протилежний, то отримаємо нерівність, рівносильну даній.
Приклад. Розв’язати нерівність 2 (2![]() 3х)
3х) ![]() 3(х + 6)
3(х + 6) ![]() 5.
5.
Розв’язання.
4 ![]() 6х
6х![]() 3х + 18
3х + 18 ![]() 5;
5;
-
3х
 6х
6х 4 + 13;
4 + 13;
-
9х
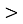 9;
9;
х![]()
![]() 1.
1.
Множиною розв’язків останньої нерівності є числовий проміжок, який позначають
(![]() ;
; ![]() 1). Точки координатної прямої, які зображують розв’зки нерівності х
1). Точки координатної прямої, які зображують розв’зки нерівності х![]()
![]() 1, розміщені ліворуч від точки
1, розміщені ліворуч від точки ![]() 1 і утворюють прмінь, у якого «виколото
1 і утворюють прмінь, у якого «виколото![]() початок.
початок.
![]() Відповідь можна записати одним зі способів (
Відповідь можна записати одним зі способів (![]() ;
; ![]() 1) або х
1) або х![]()
![]() 1.
1.
4. Осмислення матеріалу і застосування практичних дій.
Початковий рівень і середній рівень.
№115 (6![]() ).
). ![]() нерівність:
нерівність:
Розв’язання
6) ![]() 10 х
10 х ![]() 0; х
0; х![]() 0; (0;+
0; (0;+ ![]() );
);
7)![]()
![]() ; (
; (![]() ;
;
8) ![]() x
x![]()
![]() ;
; ![]() (
(![]() ;
;
9) 7х ![]() 7х
7х ![]() 21; х
21; х![]() ; (3; +
; (3; + ![]() );
);
10) 5х + 16 ![]() 6; 5х
6; 5х ![]() х
х ![]() (
(![]() ;
;
№ 118 (1,3,4). Знайти найменший цілий розв’язок нерівності:
1) 5х ![]() ; Відповідь: х
; Відповідь: х![]() ; х
; х![]()
3) ![]() Відповідь: х
Відповідь: х![]() 1,5; х = 2;
1,5; х = 2;
4) ![]() 7х
7х ![]() 15 Відповідь:
15 Відповідь: ![]()
№ 126 (4, 5, 6). Розв’язати нерівність.
4) 3![]()
![]()
![]() 3у+ 6;
3у+ 6; ![]() 11у + 3у
11у + 3у![]()
![]() 3 + 6;
3 + 6; ![]() 3;
3;
![]()
5) ![]() 2
2 ![]() ;
; ![]()
![]() 2+3; 2р
2+3; 2р ![]() 5;
5;
Відповідь: р ![]() 2,5; (
2,5; ( ![]() ).
).
6) 3m ![]() 1
1 ![]() 1,5 m + 5; 3m
1,5 m + 5; 3m ![]() 1, 5 m
1, 5 m ![]() 1+5; 1,5 m
1+5; 1,5 m![]() 6;
6;
Відповідь: m![]() 4; (
4; ( ![]()
№ 130 (3, 4). ![]() нерівність:
нерівність:
![]()
![]()
![]()
x ![]()
![]()
![]() 7х
7х ![]() 2 ;
2 ;
![]()
Достатній рівень.
№132 (2, 3, 4, 11). Розв’язати нерівності.
2) 6х![]() 3(х
3(х![]() 1)
1) ![]() 2 + 5x.
2 + 5x.
6х![]() 3х + 3
3х + 3![]() ; 6х
; 6х![]() 3х
3х![]() 2
2![]()
![]() 2x
2x![]()
Відповідь: x![]() 0,5 ;
0,5 ; ![]() ;
; ![]()
3) х![]() 2 (х
2 (х![]() 1)
1)![]() 10 + 3 (
10 + 3 (![]() х+4); х
х+4); х![]() 2х + 2
2х + 2![]() 10 +3х + 12; х
10 +3х + 12; х![]() 2х
2х![]() 3х
3х![]() 10+12
10+12![]() ;
;
![]() x
x![]() 5; (
5; (![]() ; 5
; 5![]() .
.
Відповідь: x![]() 5; (
5; (![]() ;
;![]() .
.
4) 2 (2х ![]() 3, 5)
3, 5) ![]() (2
(2![]() 3х)
3х) ![]() 6 (1
6 (1![]() х ).
х ).
4х ![]() 7
7 ![]() 6 + 9х
6 + 9х![]() 6
6 ![]() 6х ; 4х + 9х + 6х
6х ; 4х + 9х + 6х ![]() 6 + 6 +7; 19 х
6 + 6 +7; 19 х ![]() 19; х
19; х![]() 1;
1;
Відповідь: х![]() 1; (
1; (![]() ).
).
11) ![]() (9х
(9х![]() 3)
3) ![]() 1.
1.
![]() 1
1 ![]() 1.
1.
Нерівність правильна при всіх дійсних значеннях х .
Відповідь: (![]() +
+![]() ).
).
Високий рівень.
№136. Скільки цілих від’ємних розв’зків має нерівність:
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
Відповідь: ![]()
5. Історічна довідка.
Огюстен Луї Коші (1789 ![]() 1857). Видатний французький математик, автор понад 800 наукових праць. Надалі Коші працює над будівельним проектом військового порту, але, не дивлячись на всю свою зайнятість, все ж знаходить час для підготовки наукових записок з математики.
1857). Видатний французький математик, автор понад 800 наукових праць. Надалі Коші працює над будівельним проектом військового порту, але, не дивлячись на всю свою зайнятість, все ж знаходить час для підготовки наукових записок з математики.
Свої замітки він представить перед Основним відділенням (наук фізичних і математичних) Інституту Франції.
Віктор Якович Буняковський (1804 ![]() 1889). Видатний математик 19 століття народився на Вінничині . Протягом багатьох років був віце
1889). Видатний математик 19 століття народився на Вінничині . Протягом багатьох років був віце![]() президентом Петебурської академії наук. Докторська дисертація, захищена Буняковським у травні 1825 року у Паризькому університеті. Буняковський поєднував наукову діяльність із викладанням математики і механіки у кількох навчальних закладах.
президентом Петебурської академії наук. Докторська дисертація, захищена Буняковським у травні 1825 року у Паризькому університеті. Буняковський поєднував наукову діяльність із викладанням математики і механіки у кількох навчальних закладах.
У 1864 року Буняковський ![]() віце президент академії наук. У перебігу всього двадцятип’ятирічного перебування посаді віце
віце президент академії наук. У перебігу всього двадцятип’ятирічного перебування посаді віце![]() президента він продовжував відвідувати заняття і науковими дослідженями.
президента він продовжував відвідувати заняття і науковими дослідженями.
6. Вчитель. Щоб кожен учень з впевненістю міг сказати, що досяг успіху, потрібно самостійно попрацювати на виконанням аналогічних завдань.
Самостійна робота.
Варіант 1.
Середній рівень.
Розв’язати нерівності:
1). №126 (2).
6 ![]() 6х
6х![]() 10
10![]() 4х;
4х; ![]() 6х + 4х
6х + 4х![]() 10
10![]() 6;
6; ![]() 2х
2х![]() 4; х
4; х ![]()
![]() 2; (
2; (![]() ;
; ![]() 2).
2).
Відповідь: х ![]()
![]() 2; (
2; (![]() ;
; ![]() 2).
2).
№127(2).
-
35х
 28
28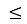 32х + 2; 35х
32х + 2; 35х 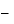 32х
32х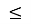 28 + 2; 3х
28 + 2; 3х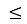 30; х
30; х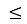 10; (
10; (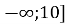 .
.
Відповідь: х![]() 10; (
10; (![]() .
.
Достатній рівень.
Розв’язати нерівності:
№132 (5, 7).
5) (х +1) (х ![]() 2)
2) ![]() (х
(х![]() 3) (х
3) (х![]() 3);
3); ![]()
![]()
![]()
![]() + 2;
+ 2; ![]()
![]()
![]() 7;
7; ![]()
![]() :
: ![]() ; [7; +
; [7; +![]() ).
).
![]()
5 (2x ![]() 1)
1) ![]() 4 (3 х
4 (3 х ![]() 5); 10х
5); 10х![]() 5
5 ![]() 12х
12х ![]() 20;
20; ![]() 2х
2х ![]() 15; х
15; х![]() 7,5;
7,5;
Відповідь: х![]() 7,5; (
7,5; (![]()
Високий рівень.
№152 (1).
Розв’язати рівняння.
1)![]() + 2x = 7;
+ 2x = 7; ![]() = 7
= 7 ![]() 2x; 7
2x; 7 ![]() 2x
2x ![]() 0;
0; ![]() 2x
2x![]()
![]() x
x ![]() 3,5 ;
3,5 ;
x![]() = 7
= 7 ![]() 2x; або x
2x; або x![]() 7
7 ![]() 2x;
2x;
3х = 2; ![]() ;
;
![]()
![]()
Варіант 2.
Середній рівень.
Розв’язати нерівності:
№126 (3).
6у + 8 ![]() 10у
10у ![]() 8; 6у
8; 6у ![]() 10у
10у ![]()
![]() 8
8![]() 8;
8; ![]() 4у
4у ![]()
![]() 16; у
16; у![]() 4. [4; +
4. [4; + ![]() ).
).
Відповідь: у![]() 4; [4; +
4; [4; + ![]() ).
).
№127 (3).
3х ![]() 10
10![]() 6 х + 2; 3х
6 х + 2; 3х ![]()
![]() 10 + 2;
10 + 2; ![]() 3х
3х![]() 12; х
12; х ![]() 4; (
4; (![]()
Відповідь: х ![]() 4; (
4; (![]()
Достатній рівень.
Розв’язати нерівності:
№132 (6,8).
6) ![]() ;
;
16![]() 24х + 9 + 9
24х + 9 + 9![]() + 12х + 4
+ 12х + 4 ![]() 25
25![]() + 10 х + 1;
+ 10 х + 1;
16![]() + 9
+ 9![]() 25
25![]() + 12х
+ 12х ![]() 9;
9; ![]() 22х
22х![]() 12;
12;

![]()
6 х +14 ![]() 20х + 8
20х + 8 ![]() 8
8![]() 3
3![]() + 7
+ 7 ![]() 10х +4
10х +4 ![]() 3
3![]()
![]() 11
11 ![]()
![]() 11;
11; ![]() ( 1; +
( 1; +![]() )
)
Відповідь: ![]() ( 1; +
( 1; +![]() ).
).
Високий рівень.
№152 (2). Розв’язати рівняння.
2) ![]() =
= ![]()
![]() 0;
0; ![]()
![]() ;
;
![]() =
= ![]() або
або ![]() =
= ![]() ;
;
![]() = 6;
= 6; ![]() =
= ![]() 12;
12;
![]()
![]()
Відповідь: ![]()
7. Підсумок уроку.
Ознайомилися:
1) З правилами для застосування розв’язання нерівностей, а також числових проміжків
2) Навчилися застосувати ці правила під час розв’язування нерівностей
3) Самостійно застосовували знання в стандартних і нестандартних ситуаціях і побачили важливість вивченої теми.
Завдання додому.
Опрацювати п.5. Розв’язати №115(11![]() 14), №127(1,4) , №130(1, 2), №133(3,4) №137, №139(1).
14), №127(1,4) , №130(1, 2), №133(3,4) №137, №139(1).
Література.
-
А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. Алгебра: Підручник для 9 класу загальноосвітніх навчальних закладів. Харків «Гімназія», 2010.
 248с.
248с.
- Збірник задач і завдань для тематичного оцінювання з алгебри для 9 класу, А.Г.Мерзляк, В.Б.Полонський.
- 4.Інтернет-бібліотека МЦНМО. http://ilib.mirror0.mccme.ru/


про публікацію авторської розробки
Додати розробку
