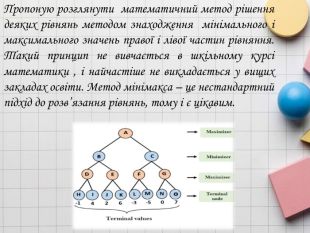
Розв'язування мінімаксних задач
Про матеріал
Мінімаксні задачі – це широкий клас задач оптимізації, де метою є знайти таке рішення, яке мінімізує максимальне значення цільової функції для найгіршого з можливих випадків. Ці задачі виникають у різних галузях, включаючи теорію ігор, економіку, інженерію та комп'ютерні науки. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку











![Приклад 1. Мінімізація максимального значення функції Задача: Знайти такі x, щоб мінімізувати максимальне значення функції f(x) = 𝑥2− 4𝑥+5 Розв’язання: Розв’язання: Знайти критичні точки функції f (x):f′(x)=2x−4 Розв’язуємо рівняння f′(x)=0:2x−4=0 ⟹ x = 2 Знайти значення функції в критичних точках:f(2) = 22−4⋅2+5=4−8+5=1 Дослідити поведінку функції на краях інтервалу: У цьому випадку ми не маємо заданого інтервалу, але для задачі можна взяти інтервал x ∈[−∞,∞]. При дуже великих або дуже малих x, f(x)→∞. Таким чином, мінімальне максимальне значення f(x) досягається в точці x=2 і дорівнює 1. Приклад 1. Мінімізація максимального значення функції Задача: Знайти такі x, щоб мінімізувати максимальне значення функції f(x) = 𝑥2− 4𝑥+5 Розв’язання: Розв’язання: Знайти критичні точки функції f (x):f′(x)=2x−4 Розв’язуємо рівняння f′(x)=0:2x−4=0 ⟹ x = 2 Знайти значення функції в критичних точках:f(2) = 22−4⋅2+5=4−8+5=1 Дослідити поведінку функції на краях інтервалу: У цьому випадку ми не маємо заданого інтервалу, але для задачі можна взяти інтервал x ∈[−∞,∞]. При дуже великих або дуже малих x, f(x)→∞. Таким чином, мінімальне максимальне значення f(x) досягається в точці x=2 і дорівнює 1.](/uploads/files/3468970/416629/472592_images/12.jpg)
![Приклад 2. Максимізація мінімального значення функції Задача: Знайти такі x, щоб максимізувати мінімальне значення функції g(x)=−𝑥2+4x−3. Розв’язання: Знайти критичні точки функції g(x):g′(x)=−2x+4 Розв’язуємо рівняння g′(x)=0:−2x+4 = 0 ⟹x=2 Знайти значення функції в критичних точках:g(2)=−(2)2+4⋅2−3=−4+8−3=1 Дослідити поведінку функції на краях інтервалу: Знову ж таки, якщо інтервал x ∈[−∞,∞], то при дуже великих або дуже малих x, g(x)→−∞. Отже, максимальне мінімальне значення g(x) досягається в точці x=2 і дорівнює 1. Приклад 2. Максимізація мінімального значення функції Задача: Знайти такі x, щоб максимізувати мінімальне значення функції g(x)=−𝑥2+4x−3. Розв’язання: Знайти критичні точки функції g(x):g′(x)=−2x+4 Розв’язуємо рівняння g′(x)=0:−2x+4 = 0 ⟹x=2 Знайти значення функції в критичних точках:g(2)=−(2)2+4⋅2−3=−4+8−3=1 Дослідити поведінку функції на краях інтервалу: Знову ж таки, якщо інтервал x ∈[−∞,∞], то при дуже великих або дуже малих x, g(x)→−∞. Отже, максимальне мінімальне значення g(x) досягається в точці x=2 і дорівнює 1.](/uploads/files/3468970/416629/472592_images/13.jpg)
![Приклад 3. Мінімізація максимального значення функції на обмеженому інтервалі Задача: Знайти такі x на інтервалі [0,3], щоб мінімізувати максимальне значення функції h(x)=𝑥3−3𝑥2+3x+1. Розв’язання: Знайти критичні точки функції ℎ(x):h′(x)=3𝑥2−6x+3 Розв’язуємо рівняння h′(x)=0:3 𝑥2 −6x+3=0 ⟹ 𝑥2 −2x+1=0 ⟹(x−1) 2 =0 ⟹x =1 Знайти значення функції в критичних точках і на кінцях інтервалу:h(0)= 03 −3⋅ 02 +3⋅0+1=1ℎ(1)= 13 −3⋅ 12 +3⋅1+1=1−3+3+1=2ℎ(3)= 33 −3⋅ 32 +3⋅3+1=27−27+9+1=10 Отже, максимальне значення h(x) на інтервалі [0,3] становить 10, а мінімальне з можливих максимальних значень досягається на інтервалі. Приклад 3. Мінімізація максимального значення функції на обмеженому інтервалі Задача: Знайти такі x на інтервалі [0,3], щоб мінімізувати максимальне значення функції h(x)=𝑥3−3𝑥2+3x+1. Розв’язання: Знайти критичні точки функції ℎ(x):h′(x)=3𝑥2−6x+3 Розв’язуємо рівняння h′(x)=0:3 𝑥2 −6x+3=0 ⟹ 𝑥2 −2x+1=0 ⟹(x−1) 2 =0 ⟹x =1 Знайти значення функції в критичних точках і на кінцях інтервалу:h(0)= 03 −3⋅ 02 +3⋅0+1=1ℎ(1)= 13 −3⋅ 12 +3⋅1+1=1−3+3+1=2ℎ(3)= 33 −3⋅ 32 +3⋅3+1=27−27+9+1=10 Отже, максимальне значення h(x) на інтервалі [0,3] становить 10, а мінімальне з можливих максимальних значень досягається на інтервалі.](/uploads/files/3468970/416629/472592_images/14.jpg)