Презентація "Урок 1. Нерівності. Системи рівнянь та нерівностей(повторення)"

Нерівності. Системи рівнянь та нерівностей (повторення)Підготовлнно: Вчитель І категорії, Тухватулліною С. А. АЛГЕБРА. 10 КЛАС. Урок №1.2024-2025

Мета уроку: систематизація та узагальнення знань, умінь і навичок з теми «Нерівності. Системи рівнянь та нерівностей»; розвивати увагу, спостережливість;виховувати пізнавальний інтерес та терпіння. Тип: повторення, систематизації знань, умінь, навичок . Обладнання: підручник, відеоуроки, онлайн тест, таблиці.

ПРОБУДЖЕННЯ…Тестова робота А. 4х²+5=10 Б. 6х-у=15; 1. Серед даних виразів слід вибрати лінійне рівняння з однією змінною. В. -5х-9=1; Г. 𝟖х+𝟏𝟏=−𝟒 2. Чи рівносильні рівняння 0· х = -7 і 0· х = 0 А. Так. Б. Ні; В. Неможливо визначити. Г. Інша відповідь 3. Серед поданих рівнянь квадратним є: А. 𝟐х𝟑−х+𝟏=0;  Б. х𝟐+𝟒х+𝟕=𝟎 В. х𝟐−𝟏𝟓=𝟎  Г. 4х – 13 = 2х + 3. Два рівняння називають рівносильними, якщо вони мають однакові розв'язки. Рівносильними вважаються і такі рівняння, які не мають коренів. Рівняння виду ax + by = c , де a, b, c — числа (коефіцієнти), x та y - змінні, називається лінійним рівнянням з двома змінними . Квадратне рівняння – це рівняння виду ax² + bx + c = 0, де коефіцієнти a, b і c – довільні числа, причому a ≠ 0 , бо інакше це буде вже не квадратне рівняння. Квадратні рівняння або не мають коренів, або мають рівно один корінь, або мають два різних

Нерівність. Основні властивості числових нерівностей. https://www.youtube.com/watch?time_continue=3&v=hs. Wv. KRJ7t. GE&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=Mjg2 Nj. Y

Основні властивості числових нерівностей. Властивість 1. Якщо a>b і b>c, тоді a>c. Це можна зобразити на числовій прямій. Перевіримо на прикладі. Нехай a = 6,b = 0,c = −4, тоді, якщо 6 > 0 і 0 > −4, тоді 6 > −4.60-4 Властивість 2. Якщо a > b, тоді a + c > b + c. Якщо до обох частин нерівності додати одне й те саме число - знак нерівності не зміниться. Властивість 3. Якщо a > b і k > 0, тоді ak > bk. Якщо обидві частини нерівності помножити на одне і те ж додатне число - знак нерівності не зміниться. Приклад: Відомо, що 17,2 < x < 17,3. Оцінити 2x. При множенні подвійної нерівності на додатне число 2, отримаємо нерівність того ж змісту (тобто знаки не зміняться).17,2 ⋅ 2 < x ⋅ 2 < 17,3 ⋅ 234,4 < 2x < 34,6

Основні властивості числових нерівностей. Властивість 4. Якщо a > b і k < 0, тоді ak < bk. Якщо обидві частини нерівності помножити на одне і теж від'ємне число - знак нерівності зміниться ( < на >, > на <)ПРИКЛАД: Відомо, що 17,2 −2x > − 34,6 − 34,6 < − 2x < −34,4 Зверни увагу!Ділення на число k можна замінити множенням на дріб 1k

2. Нерівність. Лінійні нерівності.

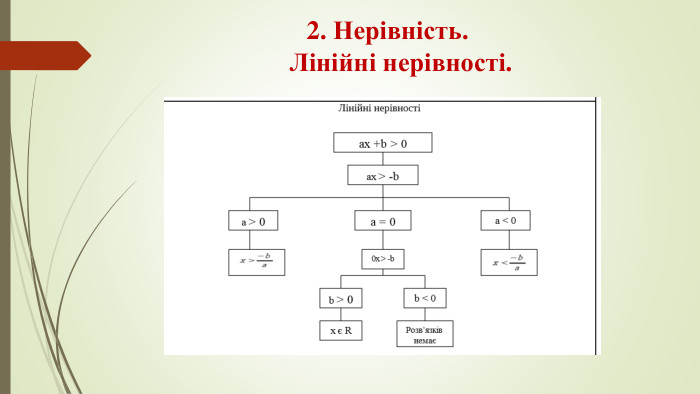
Лінійні нерівності. Лінійною нерівністю називається нерівність, яка дана або перетворена до форми ax>b або ax 0 a > 5 Відповідь: a∈(5;+∞)  2) −2y − 100 < 0 −2y < 100| : (−2)(знак нерівності змінюється на протилежний)y > 100 : (−2)y > −50 Відповідь: y∈(−50;+∞)3) − 3c ≥ −15| : (−3)(знак нерівності змінюється на протилежний)с ≤ −15 : (−3)c ≤ 5 Відповідь: c∈(−∞;5]ПРИКЛАДИ: ПАМ’ЯТАЙТЕ!Переносячи числа або букви в іншу частину нерівності, знак міняється на протилежний!

3. Нерівність. Означення квадратичної нерівності .

4. Системи двох лінійних рівнянь із двома зміннимиhttps://www.youtube.com/watch?v=Upe. Tr4bn9u8&t=1s Два рівняння з двома невідомими змінними, які описують умову однієї певної задачі, називають системою двох рівнянь з двома змінними. Систему називають лінійною, якщо всі рівняння, що входять до неї є лінійними. Загальний вигляд для двох лінійних рівнянь з двома змінними x та y: а1x + b1y + c1 = 0 і a2x + b2y + c2 = 0. Треба знайти такі значення змінних x і y, які водночас задовольняли б і перше, і друге рівняння, тобто перетворювали кожне з рівнянь у правильну рівність. Інакше кажучи:  треба знайти спільний розв'язок обох рівнянь (x;y),  або розв'язати систему даних рівнянь.

4. Системи рівнянь (нерівностей). Графічний спосіб розв’язувати системи рівнянь. Способи розв’язування системи рівнянь:а) спосіб додавання; б) спосіб підстановки. в) графічний спосіб розв’язування системи нерівностей.

Зверни увагу!Рівняння системи записують одне під одним і об'єднують спеціальним символом — фігурною дужкою:a1x+b1y+c1=0,a2x+b2y+c2=0.}Пара значень (x;y), яка одночасно є розв'язком і першого, і другого рівнянь системи, називають розв'язком системи. Розв'язати систему — це означає знайти всі її розв'язки або встановити, що їх немає. Розвязком системи рівнянь із двома змінними називають таку впорядковану пару значень змінних, які кожне рівняння системи перетворюють у правильну рівність. Приклад: Перевірити, чи є пара чисел (5;1) розв'язком системи рівнянь  x+y=6 x−y=4, підставляють значення x=5 та y=1 в кожне з рівнянь системи.5+1=65−1=4 Отримано правильні рівності, то ця пара є розв'язком системи рівнянь.}}

Алгоритм розв'язання системи двох рівнянь із двома змінними методом підстановкиhttps://www.youtube.com/watch?v=w4q. KZGQOUDM&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=Mjg2 Nj. Y Щоб розв'язати систему рівнянь способом підстановки, треба:1. Виразити з якого-небудь її рівняння одну змінну через іншу;2. Підставити в інше рівняння системи замість цієї змінної отриманий вираз;3. Розв'язати утворене рівняння з однією змінною;4. Знайти відповідне значення іншої змінної.5. Записати відповідь. Розв'язати систему рівнянь:    x−2y=3, 5x+y=4.1) З першого рівняння системи виражаємо змінну x через змінну y. Отримуємо: x−2y=3,x=3+2y; 2)  Підставимо отриманий вираз замість змінної x у друге рівняння системи: 5⋅x+y=4,5⋅(3+2y)+y=4; 3)  Розв'яжемо утворене рівняння з однією змінною, знайдемо y: 5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯. 4)  Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:   x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.5) Відповідь: (1;−1).}УВАГА!Іноді можна підставляти з одного рівняння системи в інше не значення окремої змінної, а значення цілого виразу: {x−2y=3,5(x−2y)+y=20. Можна значення x−2y з першого рівняння підставити у друге, отримавши рівняння з однією змінною: 5⋅3+y=20.

Метод алгебраїчного додавання системи двох лінійних рівнянь із двома змінними https://www.youtube.com/watch?time_continue=1&v=w4q. KZGQOUDM&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=Mz. Y4 NDIs. Mjg2 Nj. YЩоб розв’язати систему лінійних рівнянь методом додавання, треба:1) Дібравши «вигідні» множники, перетворити одне чи обидва рівняння системи так, щоб коефіцієнти при одній зі змінних стали протилежними числами;2) Додати почленно ліві й праві частини рівнянь, отриманих на першому кроці;3) Розв’язати рівняння з однією змінною, отримане на другому кроці;4) Підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи;5) Обчислити значення другої змінної та записати відповідь. Завдання 1. Розв'язати систему рівнянь   3x−y=9, 2x+y=11. Розв'язання. 1. Коефіцієнти при змінній y є протилежними числами тому додаємо почленно ліві й праві частини рівнянь.  + 3x−y=9 2x+y=11 (3x−y)+(2x+y)=9+11 3x−y+2x+y=20 5⋅x=20 x=20:5 x=42. Підставимо знайдене значення x у друге рівняння системи і знайдемо y.2⋅x+y=112⋅4+y=118+y=11y=11−8y=3  Відповідь: (4;3).}}Цей метод заснований на такому твердженні: якщо одне з рівнянь системи замінити на рівняння, отримане шляхом додавання лівих і правих частин рівнянь системи, то отримана система буде мати такі ж розв’язки, що й початкова.

ДОМАШНЯ РОБОТАВИКОНАТИ ТЕСТ: «Розв’язування систем лінійних рівнянь з двома змінними графічним способом і методом підстановки» https://naurok.com.ua/test/23-04-2024-7-kl-algebra-rozv-yazuvannya-sistem-liniynih-rivnyan-z-dvoma-zminnimi-grafichnim-sposobom-i-metodom-pidstanovki-2892730.html Перегляннути відео до уроку . Основні властивості числових нерівностей. https://www.youtube.com/watch?time_continue=3&v=hs. Wv. KRJ7t. GE&embeds_referring_euri=https%3 A%2 F%2 Fwww.miyklas.com.ua%2 F&source_ve_path=Mjg2 Nj. Y Системи двох лінійних рівнянь із двома змінними https://www.youtube.com/watch?v=Upe. Tr4bn9u8&t=1s Опрацювати презентацію до уроку.