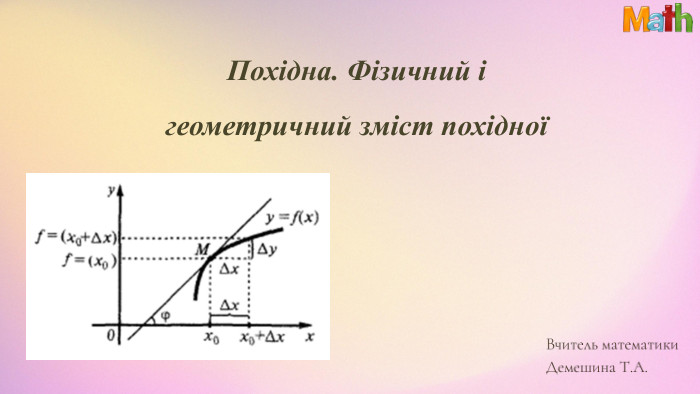
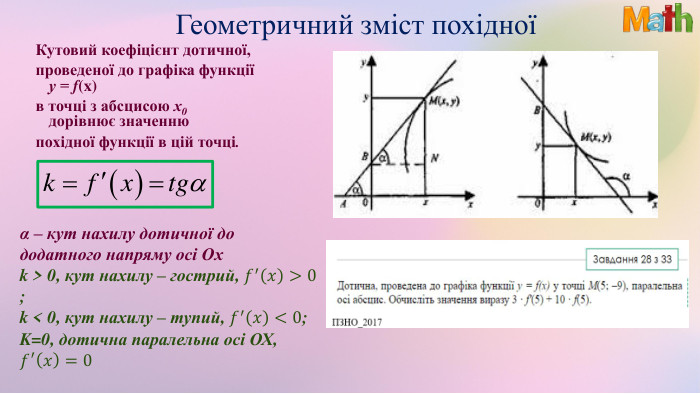
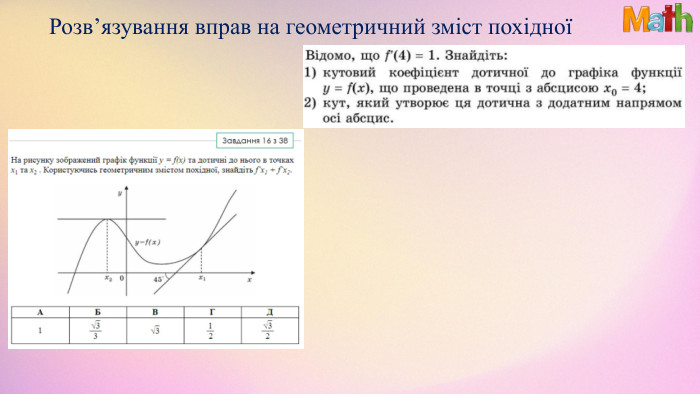
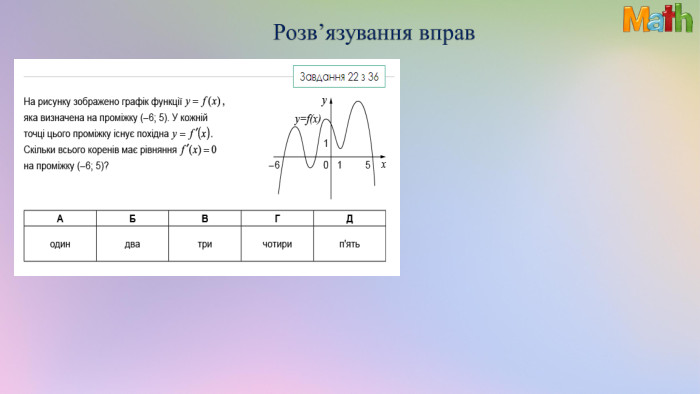
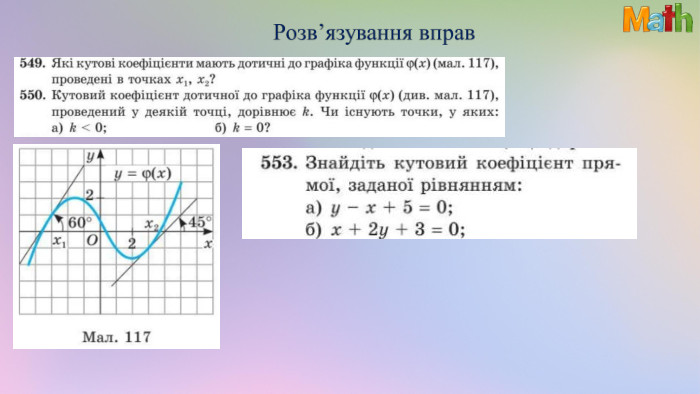
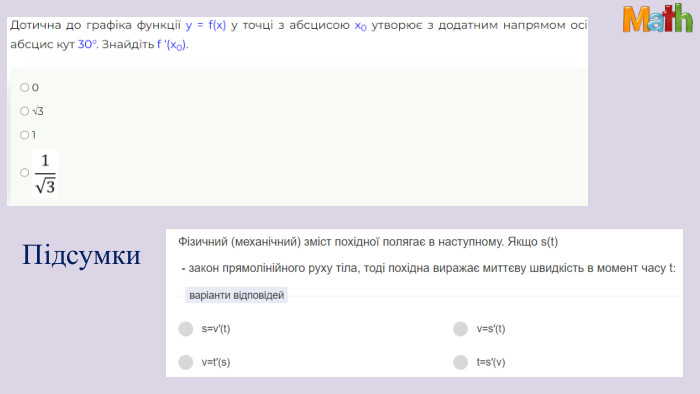
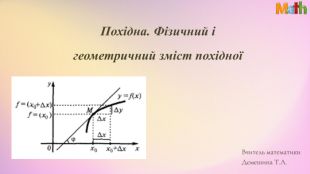
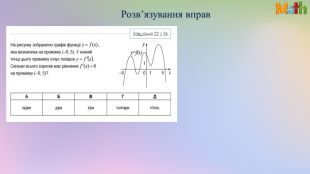
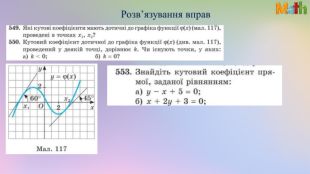
Презентація. Похідна. Геометричний та фізичний зміст похідної
Про матеріал
Матеріали презентації використовуються під час узагальнення теми "Похідна. Геометричний та фізичний зміст похідної". Використано завдання ЗНО/НМТ. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку