Розв'язування найпростіших тригонометричних рівнянь.
Розв'язування найпростіших тригонометричних рівнянь.(приклади.)
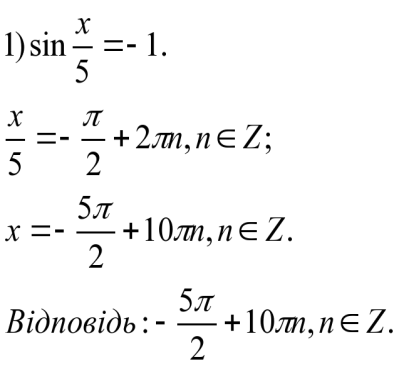
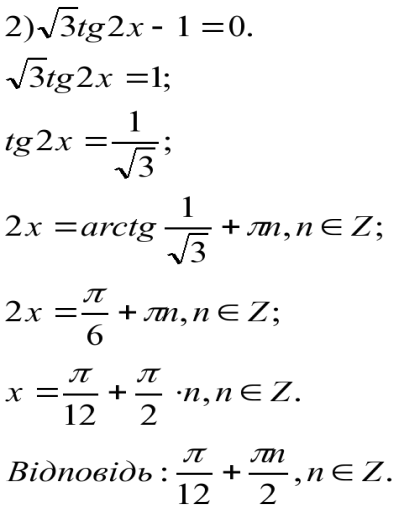
3)
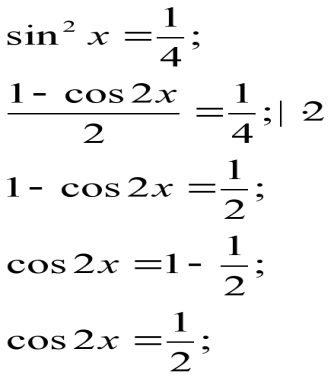
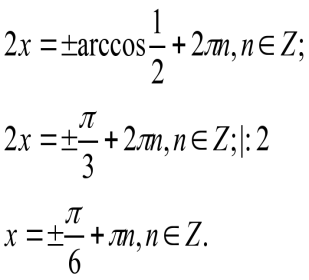
4) cos x = ![]() .
.
Розв'язання
х = ± arccos ![]() + 2πn, п
+ 2πn, п ![]() Z.
Z.
Оскільки arccos ![]() =
= ![]() , то маємо:
, то маємо:
х = ± ![]() + 2πп, п є Z.
+ 2πп, п є Z.
5) cos x = ![]() .
.
Розв'язання
Оскільки ![]() > 1, то рівняння коренів не має.
> 1, то рівняння коренів не має.
6) cos x = -![]() .
.
Розв'язання
х = ±arccos 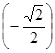 + 2πп, п
+ 2πп, п ![]() Z.
Z.
Оскільки arccos 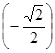 = π - arccos
= π - arccos ![]() = π -
= π - ![]() =
= ![]() , то
, то
x = ± ![]() + 2πn, n
+ 2πn, n ![]() Z.
Z.
7) tg x = ![]() .
.
Розв'язання
х =arctg![]() +πп, п
+πп, п![]() Z.
Z.
Оскільки arctg![]() =
= ![]() , то маємо:
, то маємо:
х = ![]() + πп, п
+ πп, п![]() Z.
Z.
8) ctgx – ![]() = 0.
= 0.
Розв'язання
ctg х – ![]() = 0;
= 0;
ctg х = ![]() ;
;
tg х = ![]() ,
,
x = arctg ![]() + πп ,
+ πп ,
х= ![]() + πn, n
+ πn, n ![]() Z.
Z.
9) sinх = - ![]() .
.
Розв'язання
х = (-1)n arcsin ![]() + πп, п
+ πп, п ![]() Z.
Z.
Оскільки arcsin ![]() = -
= - ![]() , то
, то
х =(-1)n ·![]() + πn, n
+ πn, n![]() Z;
Z;
х = (-1)n+1 + πп, п ![]() Z.
Z.
10) cos2x – 2 cosxsinx = 0
Розв'язання
cosx (cosx – 2 sinx) = 0
cosx = 0 або cosx – 2sinx = 0.
- cos x = 0;
x = ![]() + πп, п
+ πп, п![]() Z
Z
2) cosx – 2sinx = 0;
![]() ;
;
l – 2tgx = 0;
tgx = ![]() ;
;
x = arctg ![]() + πn, п
+ πn, п![]() Z.
Z.
Відповідь: ![]() + πn, п
+ πn, п![]() Z; arctg
Z; arctg ![]() + πn, п
+ πn, п![]() Z.
Z.
11) sin 2х — sin х = 0.
Розв'язання
sin 2х - sin х = 0;
2 sin![]() cos
cos![]() = 0;
= 0;
2 sin![]() cos
cos![]() = 0.
= 0.
-
sin
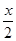 = 0;
= 0;
![]() = πn,
= πn,
х = 2πn, п![]() Z.
Z.
-
cos
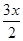 = 0,
= 0,
![]() =
= ![]() +πn,
+πn,
х = ![]() +
+![]() , п
, п ![]() Z.
Z.
Відповідь: 2πп і ![]() +
+![]() , п
, п ![]() Z.
Z.
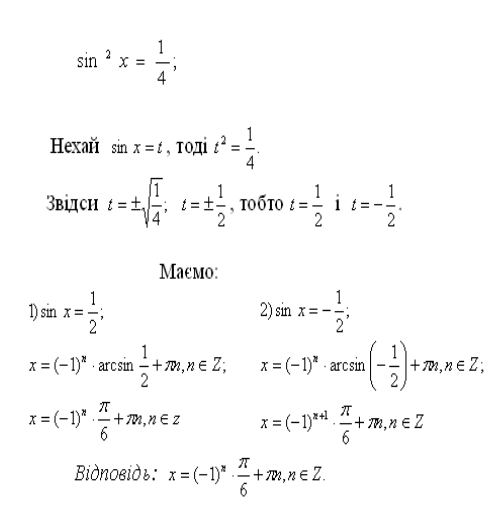 12)
12)
13) ![]() .
.
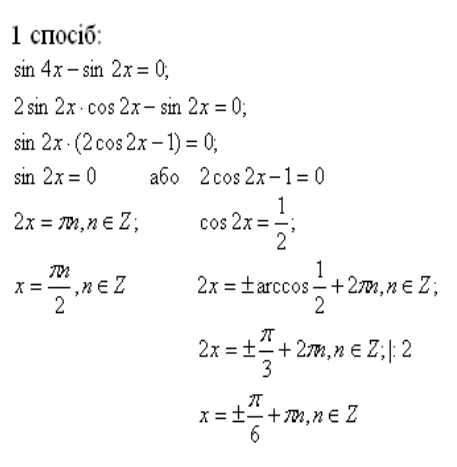
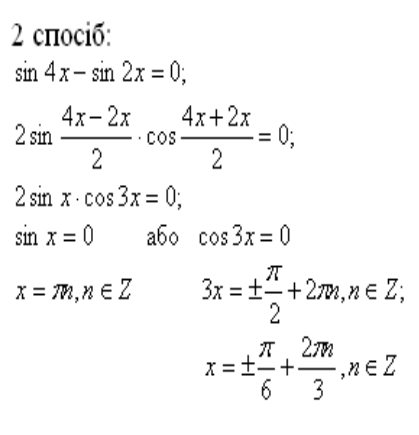


про публікацію авторської розробки
Додати розробку
