Урок алгебри у 10 класі "Найбільше та найменше значення функції на відрізку"
- к уроку.pptx pptx
- уроку.docx docx
Найбільше та найменше значення функції на відрізку
Теорема Вєйєрштрасса. Неперервна на відрізку [а; b] функція 𝒇(𝒙) має на цьому відрізку найбільше та найменше значення Карл Вєйєрштрасс
Функція 𝑓(𝑥) неперервна на відрізку [а; b] та не має на цьому відрізку критичних точок b а 𝑦=𝑓(𝑥) а b 𝑦=𝑓(𝑥) maxminmaxmin
Якщо функція 𝒇(𝒙) неперервна на відрізку [а; b] і має на ньому скінченну кількість критичних точок, то вона набуває найбільшого та найменшого значення на цьому відрізку або в критичних точках функції, які належать цьому відрізку, або на кінцях відрізка а і b
Найбільше та найменше значення функції на відрізку [а; b]1. Знайти область визначення функції 𝒇𝒙 та переконатися, що заданий відрізок входить в область визначення даної функції2. Знайти похідну 𝒇′(𝒙)3. Знайти критичні точки: 𝒇′𝒙=𝟎 або не існує4. Вибрати критичні точки, які належать заданому відрізку5. Обчислити значення функції в критичних точках та на кінцях відрізку6. Порівняти отримані значення та вибрати з них найбільше та найменше значення
Знайти найбільше та найменше значення функції 𝑓𝑥=3𝑥2−2𝑥3 на відрізку −1;2 𝑫𝒇=𝑹 . Відрізок −𝟏;𝟐 входить у область визначення функції 𝒇𝒙. Знайдемо область визначення функції 𝒇𝒙 та переконаємося, що заданий відрізок входить в область визначення даної функції 2. Знайдемо похідну 𝒇′𝒙 𝒇′𝒙=𝟔𝒙−𝟔𝒙𝟐. Похідна 𝒇′𝒙 існує на всій області визначення функції 𝒇𝒙, отже, функція 𝒇𝒙 є неперервною на даному відрізку.
Знайти найбільше та найменше значення функції 𝑓𝑥=𝟑𝑥2−𝟐𝑥3 відрізку −𝟏;𝟐 𝒇′𝒙=𝟎 𝟔𝒙−𝟔𝒙𝟐=𝟎, 𝟔𝒙𝟏−𝒙=𝟎,𝒙=𝟎, 𝒙=𝟏 3. Знайдемо критичні точки4. Знайдемо значення функції у критичних точках та на кінцях відрізку𝒇−𝟏=𝟑∙−𝟏𝟐−𝟐∙−𝟏𝟑=𝟑+𝟐=𝟓;𝒇𝟐=𝟑∙𝟐𝟐−𝟐∙𝟐𝟑=𝟏𝟐−𝟏𝟔=−𝟒;𝒇𝟎=𝟑∙𝟎−𝟐∙𝟎=𝟎;𝒇𝟏=𝟑∙𝟏𝟐−𝟐∙𝟏𝟑=𝟑−𝟐=𝟏. 𝒎𝒂𝒙−𝟏;𝟐𝒇𝒙=𝒇−𝟏=𝟓 𝒎𝒊𝒏−𝟏;𝟐𝒇𝒙=𝒇𝟐=−𝟒 Обидві критичні точки належать відрізку −𝟏;𝟐
Знайти найбільше та найменше значення функції 𝑓𝑥=𝑥𝟒−𝟒𝑥3+𝟏 на відрізку −𝟏;𝟏 𝑫𝒇=𝑹 . Відрізок −𝟏;𝟏 входить у область визначення функції 𝒇𝒙. Знайдемо область визначення функції 𝒇𝒙 та переконаємося, що заданий відрізок входить в область визначення даної функції 2. Знайдемо похідну 𝒇′𝒙 𝒇′𝒙=𝟒𝒙𝟑−𝟏𝟐𝒙𝟐. Похідна 𝒇′𝒙 існує на всій області визначення функції 𝒇𝒙, отже, функція 𝒇𝒙 є неперервною на даному відрізку.
𝒇′𝒙=𝟎 𝟒𝒙𝟑−𝟏𝟐𝒙𝟐=𝟎, 𝟒𝒙𝟐𝒙−𝟑=𝟎,𝒙=𝟎, 𝒙=𝟑 3. Знайдемо критичні точки4. Знайдемо значення функції у критичній точці х = 0 та на кінцях відрізку𝒇−𝟏=−𝟏𝟒−𝟒∙−𝟏𝟑+𝟏=𝟔;𝒇𝟎=𝟎−𝟒∙𝟎+𝟏=𝟏;𝒇𝟏=𝟏𝟐−𝟒∙𝟏𝟑+𝟏=−𝟒+𝟐=−𝟐. 𝒎𝒂𝒙−𝟏;𝟏𝒇𝒙=𝒇−𝟏=𝟔 𝒎𝒊𝒏−𝟏;𝟏𝒇𝒙=𝒇𝟏=−𝟐 Знайти найбільше та найменше значення функції 𝑓𝑥=𝑥𝟒−𝟒𝑥3+𝟏 на відрізку −𝟏;𝟏 Точка х = 3 не належить відрізку −𝟏;𝟏
Знайти найбільше та найменше значення функції 𝑓𝑥=𝟓𝒔𝒊𝒏𝒙+𝒄𝒐𝒔𝟐𝒙 на відрізку 𝟎;𝝅 𝑫𝒇=𝑹 . Відрізок 0;𝜋 входить у область визначення функції 𝒇𝒙. Знайдемо область визначення функції 𝒇𝒙 та переконаємося, що заданий відрізок входить в область визначення даної функції 2. Знайдемо похідну 𝒇′𝒙 𝒇′𝒙=𝟓𝒄𝒐𝒔𝒙−𝟐𝒔𝒊𝒏𝟐𝒙. Похідна 𝒇′𝒙 існує на всій області визначення функції 𝒇𝒙, отже, функція 𝒇𝒙 є неперервною на заданому відрізку.
𝒇′𝒙=𝟎 𝟓𝒄𝒐𝒔𝒙−𝟐𝒔𝒊𝒏𝟐𝒙=𝟎𝟓𝒄𝒐𝒔𝒙−𝟐∙𝟐𝒔𝒊𝒏𝒙𝒄𝒐𝒔𝒙=𝟎,𝒄𝒐𝒔𝒙𝟓−𝟒𝒔𝒊𝒏𝒙=𝟎𝒄𝒐𝒔𝒙=𝟎 або 𝟓−𝟒𝒔𝒊𝒏𝒙=𝟎 𝒙=𝝅𝟐+𝝅𝒏, 𝒏∈𝒁 𝟒𝒔𝒊𝒏𝒙=𝟓 𝒔𝒊𝒏𝒙=𝟓𝟒<𝟏− рівняння коренів немає, так як −𝟏≤𝒔𝒊𝒏𝒙≤𝟏 3. Знайдемо критичні точки. Знайти найбільше та найменше значення функції 𝑓𝑥=𝟓𝒔𝒊𝒏𝒙+𝒄𝒐𝒔𝟐𝒙 на відрізку 𝟎;𝝅
n = 0 𝒙=𝝅𝟐+𝝅∙𝟎=𝝅𝟐n = 1 𝒙=𝝅𝟐+𝝅∙𝟏=𝟑𝝅𝟐n = ‒1 𝒙=𝝅𝟐+𝝅∙−𝟏=𝝅𝟐−𝝅=−𝝅𝟐 Так как рівняння 𝒄𝒐𝒔𝒙=𝟎 має безліч коренів, знайдемо критичні точки, які належать відрізку 𝟎;𝝅. Знайти найбільше та найменше значення функції 𝑓𝑥=𝟓𝒔𝒊𝒏𝒙+𝒄𝒐𝒔𝟐𝒙 на відрізку 𝟎;𝝅 До відрізка 𝟎;𝝅 належить тільки одна критична точка 𝒙=𝝅𝟐 Для цього знайдемо значення 𝒙=𝝅𝟐+𝝅𝒏, 𝒏∈𝒁 при n = 0, 1, ‒1
4. Знайдемо значення функції у критичній точці 𝒙=𝜋2 та на кінцях відрізку 𝒎𝒂𝒙𝟎;𝝅𝒇𝒙=𝒇𝝅𝟐=𝟒 𝒎𝒊𝒏𝟎;𝝅𝒇𝒙=𝒇𝝅=−𝟏 Знайти найбільше та найменше значення функції 𝑓𝑥=𝟓𝒔𝒊𝒏𝒙+𝒄𝒐𝒔𝟐𝒙 на відрізку 𝟎;𝝅 𝒇𝟎=𝟓𝒔𝒊𝒏𝟎+𝒄𝒐𝒔𝟎=𝟎+𝟏=𝟏;𝒇𝝅=𝟓𝒔𝒊𝒏𝝅+𝒄𝒐𝒔𝟐𝝅=𝟓∙𝟎−𝟏=−𝟏;𝒇𝝅𝟐=𝟓𝒔𝒊𝒏𝝅𝟐+𝒄𝒐𝒔𝟐𝝅𝟐=𝟓𝒔𝒊𝒏𝝅𝟐+𝒄𝒐𝒔𝝅=𝟓∙𝟏−𝟏=𝟒.
Запишіть число 10 у вигляді суми двох невід’ємних доданків так, щоб сума квадратів цих чисел була найменшою Нехай одне число буде х ≥ 0, тоді друге – (𝟏𝟎−𝒙). 1) Запишемо суму квадратів цих чисел: 𝒙𝟐+(𝟏𝟎−𝒙)𝟐. 2) Розглянемо функцію 𝒇𝒙=𝒙𝟐+(𝟏𝟎−𝒙)𝟐 на відрізку [0;10] і дослідимо її на найменше та найбільше значення на даному відрізку.
Запишіть число 10 у вигляді суми двох невід’ємних доданків так, щоб сума квадратів цих чисел була найменшою3) Знайдемо похідну цієї функції та критичні точки𝒇′𝒙=𝟐𝒙+𝟐𝟏𝟎−𝒙∙−𝟏==𝟐𝒙−𝟐𝟏𝟎−𝒙==𝟐𝒙−𝟐𝟎+𝟐𝒙=𝟒𝒙−𝟐𝟎𝒇′𝒙=𝟎 𝟒𝒙−𝟐𝟎=𝟎𝒙=𝟓 - одна критична точка 4) Знайдемо значення функції в критичній точці 𝒙=𝟓 та на кінцях відрізку 𝒇𝟓=𝟐𝟓+(𝟏𝟎−𝟓)𝟐=𝟓𝟎;𝒇𝟎=𝟎+(𝟏𝟎−𝟎)𝟐=𝟏𝟎𝟎;𝒇𝟏𝟎=𝟏𝟎𝟐+(𝟏𝟎−𝟏𝟎)𝟐=𝟏𝟎𝟎. 𝒎𝒊𝒏𝟎;𝟏𝟎𝒇𝒙=𝒇𝟓=𝟓𝟎 Значить перший доданок дорівнює 5, другий 10 – 5 = 5. Відповідь: 10 = 5 + 5
Для виготовлення акваріуму Петрик взяв прямокутний шматок скла завдовжки 80 см і завширшки 50 см і розрізав його так, як зображено на малюнку. Після вилучення чотирьох однакових кутових квадратів акваріум біло склеєно. Який найбільший об’єм (в літрах) може мати акваріум Петрика?Нехай від кожної сторони відрізали квадрат зі стороною х см, х > 0. Тоді сторони акваріуму будуть дорівнювати (𝟖𝟎 – 𝟐𝒙) см та (𝟓𝟎 – 𝟐𝒙) см. хх80 см50 см. Об’єм акваріуму 𝑽=𝒙𝟖𝟎 – 𝟐𝒙𝟓𝟎 – 𝟐𝒙==𝒙𝟒𝟎𝟎𝟎−𝟏𝟎𝟎𝒙−𝟏𝟔𝟎𝒙+𝟒𝒙𝟐==𝟒𝟎𝟎𝟎𝒙−𝟐𝟔𝟎𝒙𝟐+𝟒𝒙𝟑..
Розглянемо отриману функцію 𝑽𝒙=𝟒𝟎𝟎𝟎𝒙−𝟐𝟔𝟎𝒙𝟐+𝟒𝒙𝟑 на відрізку [0; 25] Знайдемо похідну та критичні точки отриманої функції𝑽′𝒙=𝟒𝟎𝟎𝟎−𝟓𝟐𝟎𝒙+𝟏𝟐𝒙𝟐𝑽′𝒙=𝟎𝟒𝟎𝟎𝟎−𝟓𝟐𝟎𝒙+𝟏𝟐𝒙𝟐=𝟎:𝟒𝟑𝒙𝟐−𝟏𝟑𝟎𝒙+𝟏𝟎𝟎𝟎=𝟎𝑫𝟏=𝟔𝟓𝟐−𝟑∙𝟏𝟎𝟎𝟎=𝟏𝟐𝟐𝟓=𝟑𝟓𝟐>𝟎𝒙𝟏,𝟐=𝟔𝟓∓𝟑𝟓𝟑𝒙𝟏=𝟔𝟓+𝟑𝟓𝟑=𝟏𝟎𝟎𝟑=𝟑𝟑𝟏𝟑− не входить до заданого відрізку [0; 25]𝒙𝟐=𝟔𝟓−𝟑𝟓𝟑=𝟑𝟎𝟑=𝟏𝟎 𝑽𝟎=𝟎𝑽𝟏𝟎=𝟏𝟎∙𝟖𝟎 – 𝟐∙𝟏𝟎𝟓𝟎 – 𝟐∙𝟏𝟎=𝟏𝟎∙𝟔𝟎∙𝟑𝟎=𝟏𝟖𝟎𝟎𝑽𝟐𝟓=𝟐𝟓∙𝟖𝟎 – 𝟐∙𝟐𝟓𝟓𝟎 – 𝟐∙𝟐𝟓=𝟎 Знайдемо значення функції 𝑽𝒙 у точці х = 10 та на кінцях відрізку тобто найбільший об’єм акваріуму Петрика може дорівнювати 1800 м3 = 18 літрам. Тоді 𝒎𝒂𝒙𝟎;𝟐𝟓𝑽𝒙=𝑽𝟏𝟎=𝟏𝟖𝟎𝟎,
На сторінці текст займає площу 384 см2. Верхнє та нижнє поля повинні бути по 2 см, а праве та ліве – по 3 см. Які розміри повинна мати сторінка з точки зору економії паперу?Нехай ширина тексту х см, тоді його довжина - 𝟑𝟖𝟒𝒙 см. Довжина сторінки, враховуючи верхнє та нижнє поле по 2 см, дорівнює (𝒙+𝟒)см, аналогічно ширина (𝟑𝟖𝟒𝒙+𝟔) см, де 𝒙∈[𝟎;+∞) Тоді площа сторінки 𝑺𝒙=𝒙+𝟒𝟑𝟖𝟒𝒙+𝟔=𝟑𝟖𝟒+𝟏𝟓𝟑𝟔𝒙+𝟔𝒙+𝟐𝟒=1536𝑥+6𝑥+408 см2.
Знайдемо похідну 𝑺′𝒙 та критичні точки 𝑺′𝒙=−𝟏𝟓𝟑𝟔𝒙𝟐+𝟔𝑺′𝒙=𝟎−𝟏𝟓𝟑𝟔𝒙𝟐+𝟔=𝟎, −𝟏𝟓𝟑𝟔+𝟔𝒙𝟐=𝟎, 𝒙𝟐=𝟐𝟓𝟔, 𝒙=𝟏𝟔 та 𝒙=−𝟏𝟔 – не входить до заданого відрізка З’ясуємо, якого знаку набуває похідна на заданому відрізку. Розв’яжемо нерівності −𝟏𝟓𝟑𝟔+𝟔𝒙𝟐>𝟎 та −𝟏𝟓𝟑𝟔+𝟔𝒙𝟐<𝟎 𝑺′𝒙 ‒‒+х 0 16maxmin. Знайдемо значення функції в точці 𝒙=𝟏𝟔. 𝑺𝟏𝟔=𝟏𝟔+𝟒𝟑𝟖𝟒𝟏𝟔+𝟔=30∙20 Тобто з точки зору економії паперу розмір аркуша повинен бути 30×20 см.
Слайд Найбільше та найменше значення функції на відрізку
Знову рада вітати вас у нашому класі. Задачі на пошук оптимального рішення займають значне місце в практичному житті людини. Наприклад, яку кількість продукції треба виготовити підприємству, щоб отримати найбільший прибуток? Як, маючи обмежені ресурси, виконати виробниче завдання у найкоротшій час? Як організувати доставку товару в торгівельні точки так, щоб витрати палива були найменшими? Частину таких задач допомагають розв’язати методи математичного аналізу. Це ті задачі, які можна звести до знаходження найбільшого та найменшого значення функції.
Сьогодні на уроці ми з’ясуємо, чи можна знайти найбільше та найменше значення функції на відрізку [а; b], однак обмежимося розглядом лише диференційованих функцій, тобто тих функцій, які мають похідну.
Слайд Скористаємося теоремою Вейєрштраса: Неперервна на відрізку [а; b] функція 
має на цьому відрізку найбільше та найменше значення, тобто існують точки відрізка [а; b], в яких функція набуває найбільшого та найменшого на [а; b] значення.
Слайд Розглянемо декілька випадків.
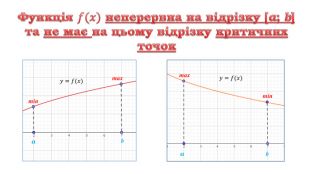
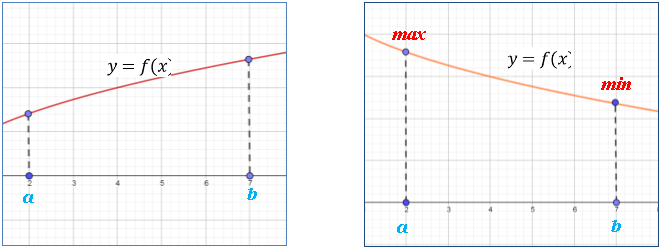1. Неперервна на відрізку [а; b] функція не має на цьому відрізку критичних точок. Тоді на цьому відрізку похідна 
зберігає свій постійний знак, тобто функція або зростає, або спадає. Тому найбільше і найменше значення функції на відрізку [а; b] – це значення функції на кінцях відрізку в точках а и b
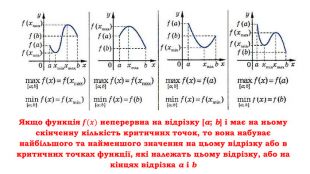
Слайд Розглянемо наведені малюнки. Якщо функція
неперервна на відрізку [а; b] і має на ньому скінченну кількість критичних точок, то вона набуває найбільшого та найменшого значення на цьому відрізку або в критичних точках функції, які належать цьому відрізку, або на кінцях відрізка а і b
Хочу зауважити, що для використання цих орієнтирів необхідно переконатися, що заданий відрізок належить області визначення функції та що функція неперервна на цьому відрізку
Слайд Таким чином, щоб знайти найбільше та найменше значення функції на проміжку [а; b] , можна користуватися наступною схемою:
1. Знайти область визначення функції та переконатися, що заданий відрізок входить в область визначення даної функції
2. Знайти похідну 
3. Знайти критичні точки: 
або не існує
4. Вибрати критичні точки, які належать заданому відрізку
5. Обчислити значення функції в критичних точках та на кінцях відрізку
6. Порівняти отримані значення та вибрати з них найбільше та найменше значення
Слайд Розглянемо приклади
Приклад 1. Знайти найбільше та найменше значення функції 
на відрізку
Клик Знайдемо область визначення функції та переконаємось, що заданий відрізок входить в область визначення даної функції
Клик Дана функція задана многочленом, значить вона визначена на множині всіх дійсних чисел, тобто 
.
Клик Відрізок 
входить у область визначення функції .
Клик Знайдемо похідну 
.
Клик Похідна існує на всій області визначення функції , отже, функція
є неперервною на даному відрізку.
Слайд Знайдемо критичні точки функції: 
,
Клик Обидві критичні точки належать відрізку.
Клик Знайдемо значення функції у критичних точках та на кінцях відрізку. Для цього підставимо значення - 1, 2, 0 і 1 у рівняння нашої функції. Отримаємо Клик
.
Порівняємо отримані значення та запишемо відповідь.
Як бачимо, найбільшого значення функція набуває при х = ‒1. Найменшого ‒ при х = 2. Клик Значить 
Слайд Приклад 2. Знайти найбільше та найменше значення функції 
на відрізку 
Клик Знайдемо область визначення функції та переконаємось, що заданий відрізок входить в область визначення даної функції . Дана функція задана многочленом, значить вона визначена на множині всіх дійсних чисел, тобто .
Клик Відрізок входить у область визначення функції .
Клик Знайдемо похідну 
.
Клик Похідна існує на всій області визначення функції , отже, функція є неперервною на даному відрізку.
Слайд Знайдемо критичні точки:
,
Клик Точка х = 3 не належить відрізку
.
Клик Знайдемо значення функції в критичній точці х = 0 та на кінцях відрізку. Для цього підставимо значення ‒1, 0 і 1 у рівняння даної функції.
Клик 
.
Порівняємо отримані значення та запишемо відповідь. Як бачимо, у цьому прикладі найбільшого значення функція набуває при х = ‒1. Найменшого ‒ при х = 1.
Клик Значить 
Слайд Приклад 3. Знайти найбільше та найменше значення функції 
на відрізку 
Знайдемо область визначення функції та переконаємося, що заданий відрізок входить в область визначення даної функції .
Клик Дана функція визначена на множині всіх дійсних чисел, тобто .
Клик Відрізок входить у область визначення функції .
Клик Знайдемо похідну 
.
Клик Похідна існує на всій області визначення функції , отже, функція є неперервною на даному відрізку.
Слайд Знайдемо критичні точки:
Клик Отримуємо 
,
рівняння коренів немає, бо 
Слайд
Так как рівняння 
має безліч коренів, знайдемо критичні точки, які належать відрізку .
Клик Для цього знайдемо значення при n = 0, 1, ‒1
n = 0 
n = 1 
n = ‒1 
клик Як бачимо до відрізка належить тільки одна критична точка 
Слайд Знайдемо значення функції в критичній точці та на кінцях відрізку
Клик 
.
Порівняємо отримані значення та запишемо відповідь.
Як бачимо, найбільшого значення функція набуває при х = 
. Найменшого ‒ при х = 
. Клик Значить 
Слайд Запишіть число 10 у вигляді суми двох невід’ємних доданків так, щоб сума квадратів цих чисел була найменшою
Клик Нехай одне невід’ємне число буде х, тоді друге – (10 – х).
Клик Запишемо суму квадратів цих чисел: 
.
Клик Розглянемо функцію 
на відрізку [0;10] і дослідимо її на найменше та найбільше значення на даному відрізку.
Слайд Знайдемо похідну цієї функції та критичні точки
Клик
Клик 
Функція має єдину критичну точку х = 5
Клик Знайдемо значення функції в критичних точках та на кінцях відрізку, підставивши значення х = 5, 0 та 10 у рівняння функції
Клик
.
Клик 
.
Клик Значить перший доданок дорівнює 5, другий 10 – 5 = 5.
Клик Відповідь: 10 = 5 + 5
Слайд Приклад 5. Для виготовлення акваріуму Петрик взяв прямокутний шматок скла завдовжки 50 см і завширшки 80 см і розрізав його так, як зображено на малюнку. Після вилучення чотирьох однакових кутових квадратів акваріум біло склеєно. Який найбільший об’єм ( літрах) може мати акваріум Петрика?
Хочу зауважити, що подібні задачі зустрічаються у завданнях зовнішнього незалежного тестування минулих років.
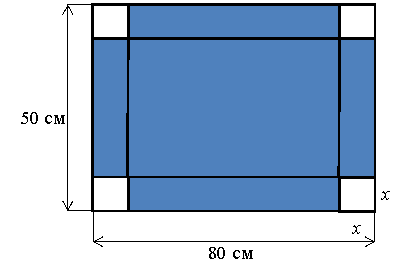Клик Нехай від кожної сторони відрізали квадрат зі стороною х см, х > 0. Тоді сторони акваріуму будуть дорівнювати (
) см та (
) см.
Об’єм акваріуму
.
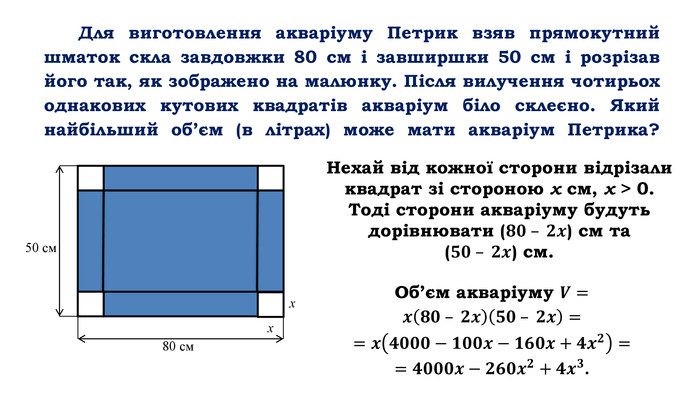
Слайд Розглянемо отриману функцію
на відрізку [0; 25] і дослідимо її на найменше та найбільше значення на даному відрізку.
Клик Знайдемо похідну та критичні точки отриманої функції
Ділимо обидві частини рівняння на 4.
Отримаємо 
Розв’яжемо отримане квадратне рівняння, використовуючи формулу дискримінанта та коренів квадратного рівняння, якщо коефіцієнт b - парний
не входить до заданого відрізку [0; 25] 
Клик Знайдемо значення функції 
у точці х = 10 на кінцях відрізку підставивши значення х = 25, 0 та 10 у рівняння функції
Клик Тоді 
,
Клик тобто найбільший об’єм акваріуму Петрика може дорівнювати 1800 м3 = 18 літрам
Слайд Приклад 6 На сторінці текст займає площу 384 см2. Верхнє та нижнє поля повинні бути по 2 см, а праве та ліве – по 3 см. Які розміри повинна мати сторінка з точки зору економії паперу?
Клик Нехай ширина тексту х см, тоді його довжина - 
см.
Клик Довжина сторінки, враховуючи верхнє та нижнє поле по 2 см, дорівнює (
см, аналогічно ширина (
см, де 
Клик Тоді площа сторінки 
см2.
Слайд
Клик Знайдемо похідну 
та критичні точки
Клик 
,
, 
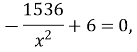
та 
– не входить до заданого відрізка
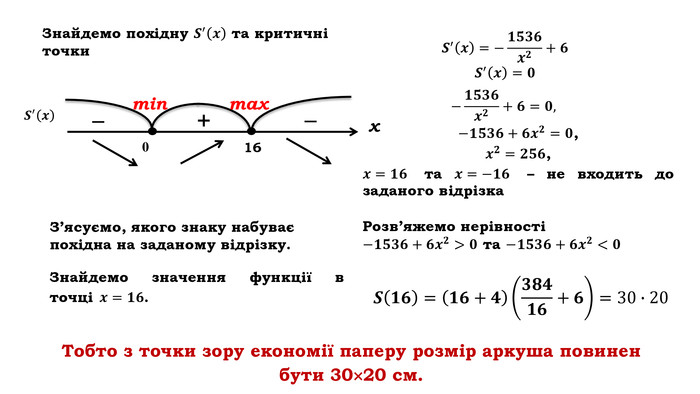
З’ясуємо, якого знаку набуває похідна на заданому відрізку. Для цього розв’яжемо нерівності 
та 
методом інтервалів. Розставимо знаки похідної, враховуючи властивості квадратичної функції та значення коефіцієнта а, з’ясуємо проміжки монотонності функції та знайдемо точки екстремуму функції.
Клик Отримаємо
Тобто – точка максимуму.
Клик Знайдемо значення функції в точці
. 
Клик Тобто з точки зору економії паперу розмір аркуша повинен бути 30 ×20 см.
Шановні десятикласники та десятикласниці! Алгебра і початки аналізу – корисний і дуже цікавий навчальний предмет. Він розвиває аналітичне й логічне мислення, дослідницькі навички, математичну культуру, кмітливість.
У нас час немає такої галузі науки, де не застосовують досягнень математики. У фізиці та хімії, біології та астрономії, у географії та економіці і навіть у лігвістиці використовують так званий «математичний інструмент». Дуже сподіваюся, що мої уроки допоможуть вам отримати ґрунтовні математичні знання з теми «Дослідження функцій».
А на сьогодні наш з вами урок закінчено. Я не прощаюся з вами, а тільки кажу вам «до побачення». До нових зустрічей
про публікацію авторської розробки
Додати розробку