Урок у 10 класі "Застосування похідної до дослідження функції та побудови її графіка"
Про матеріал
Даний матеріал призначений для використання на уроках алгебри 10 класу, в якому викладається математика за рівнем стандарту. Цей урок був проведений в прямому ефірі телеканалу Дніпро ТВ 27 березня 2020 року (як дистанційна робота під час карантину). Переглянути відео даного уроку можна за посиланням https://www.youtube.com/watch?v=s5S5IxPA1rs&list=PLwoQuBQSt2ivci6K9QNo2Kg2mWd3aWyhU&index=8&t=0s Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





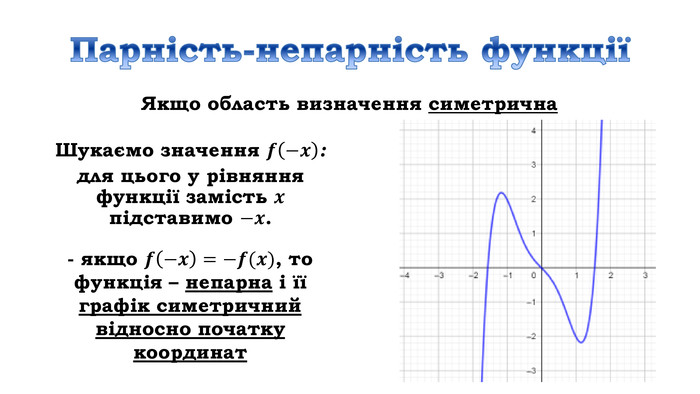
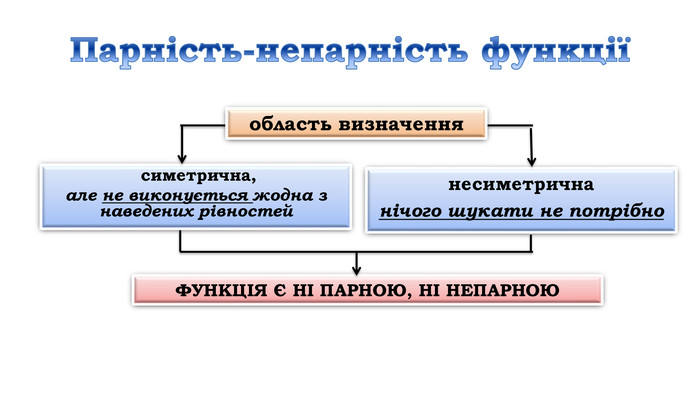
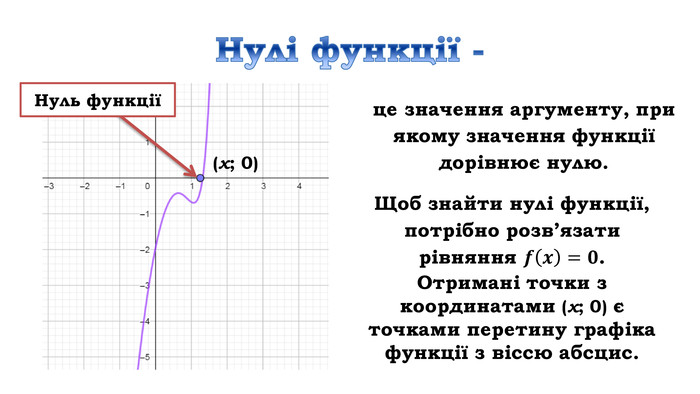
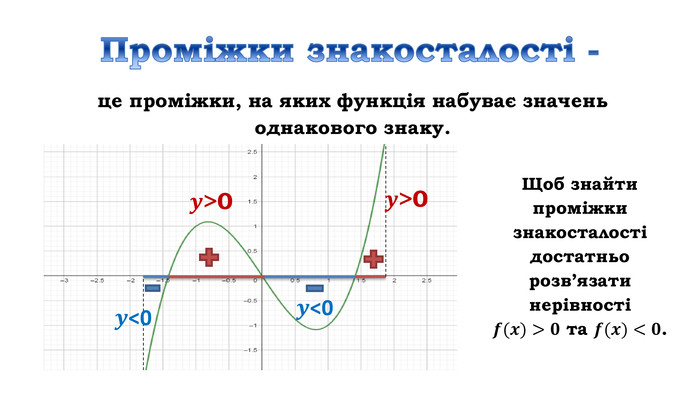
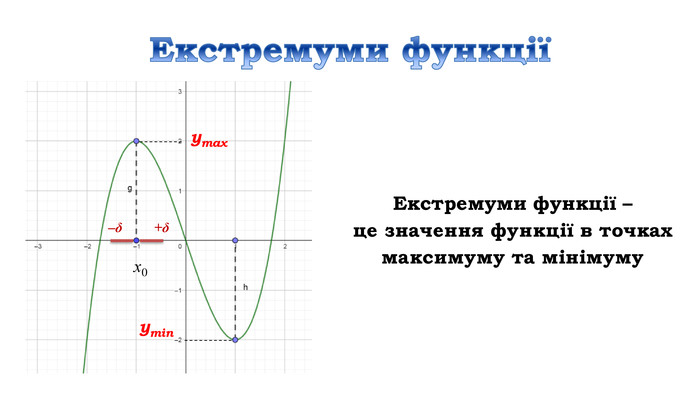
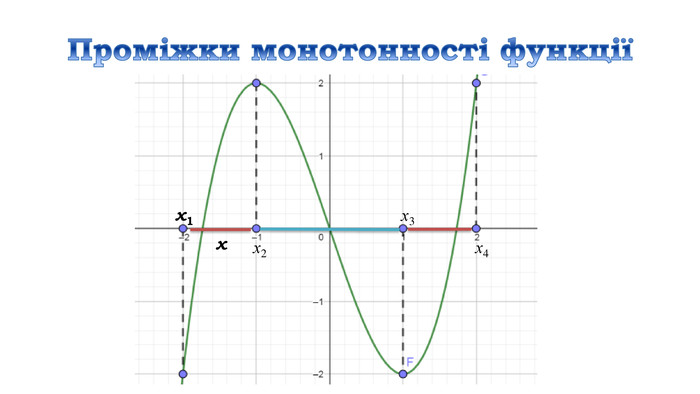
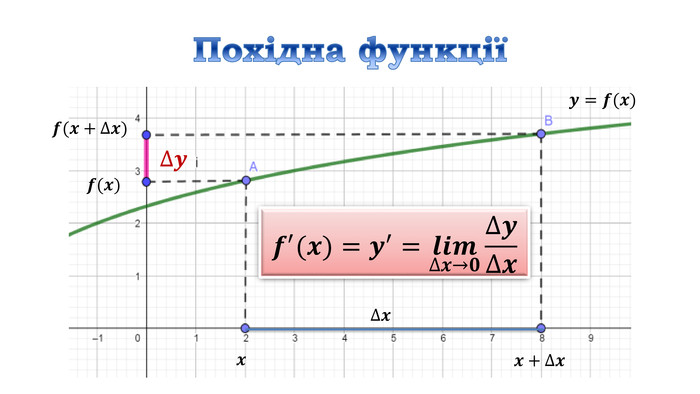


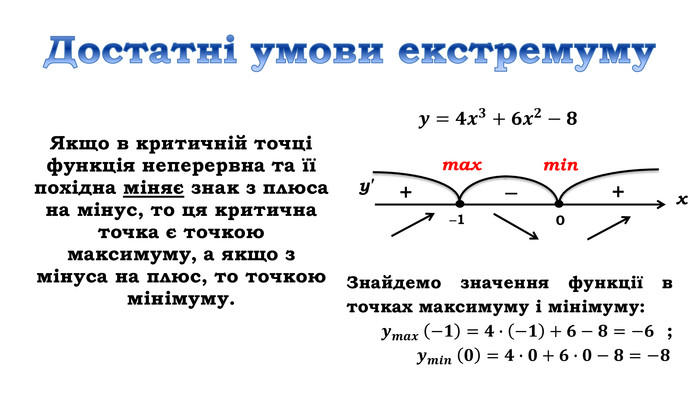
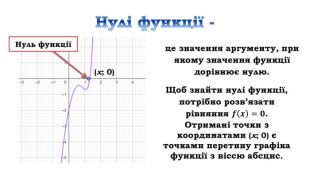
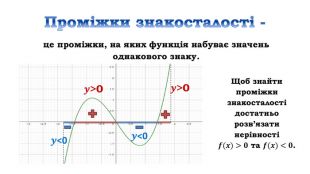
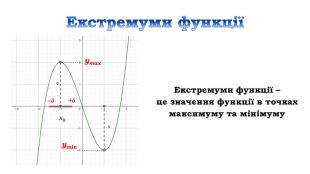
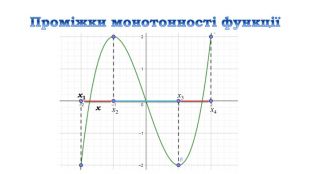
![Дослідити функцію 𝑦=4𝑥3+6𝑥2−8 на монотонність Знайдемо область визначення функціїD (у) = R𝒚′=𝟏𝟐𝒙𝟐+𝟏𝟐𝒙=𝟏𝟐𝒙(𝒙+𝟏) 𝟏𝟐𝒙𝒙+𝟏=𝟎, 𝒙=𝟎, 𝒙=−𝟏 2) Знайдемо похідну3) Знайдемо критичні точки 4) Позначимо критичні точки на області визначення функції та знайдемо знак похідної на кожному з отриманих проміжків.𝟏𝟐𝒙(𝒙+𝟏)>𝟎, 𝟏𝟐𝒙𝒙+𝟏<𝟎 х проміжки: зростання 𝒙∈−∞;−𝟏]∪[𝟎;+∞), спадання 𝒙∈[−𝟏; 𝟎] Дослідити функцію 𝑦=4𝑥3+6𝑥2−8 на монотонність Знайдемо область визначення функціїD (у) = R𝒚′=𝟏𝟐𝒙𝟐+𝟏𝟐𝒙=𝟏𝟐𝒙(𝒙+𝟏) 𝟏𝟐𝒙𝒙+𝟏=𝟎, 𝒙=𝟎, 𝒙=−𝟏 2) Знайдемо похідну3) Знайдемо критичні точки 4) Позначимо критичні точки на області визначення функції та знайдемо знак похідної на кожному з отриманих проміжків.𝟏𝟐𝒙(𝒙+𝟏)>𝟎, 𝟏𝟐𝒙𝒙+𝟏<𝟎 х проміжки: зростання 𝒙∈−∞;−𝟏]∪[𝟎;+∞), спадання 𝒙∈[−𝟏; 𝟎]](/uploads/files/312761/162672/175277_images/14.jpg)
















-

Клепікова Ольга Анатоліївна
21.05.2024 в 00:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Харченко Ірина Вікторівна
13.05.2024 в 10:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гозян Тетяна
04.05.2024 в 23:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
01.04.2024 в 18:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
09.05.2023 в 22:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Овсянка Галина
16.12.2022 в 21:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самарченко Інна Вікторівна
01.11.2022 в 15:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дятленко Надія Анатоліївна
11.05.2022 в 22:07
Дякую! Хороша робота!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кравець Андрея Іванівна
25.04.2022 в 22:27
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гордієць Тамара Степанівна
30.03.2021 в 06:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дмитренко Олена Борисівна
14.08.2020 в 11:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Асламова Любов Володимирівна
14.04.2020 в 10:58
Загальна:
1.0
Структурованість
1.0
Оригінальність викладу
1.0
Відповідність темі
1.0
Показати ще 9 відгуків