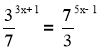Розв’язування показникових рівнянь

 

 

 

 

 

 

Тема уроку

 

Розв’язування показникових рівнянь

Урок алгебри у 11 класі з використанням інтерактивних технологій

 

 

 

Учителя математики

НВК №2 м. Немирова

Капітули Оксани Григорівни

 

 

 

 

 

 

 

Тема: Розв’язування показникових рівнянь.   11 клас  

Узагальнення – це мабуть,

Найлегший і найочевидніший шлях

Розширення математичних знань.

В. Сойер.

 

Мета: узагальнити і поглибити знання з теми «Показникові рівняння», удосконалити навички розв’язувати показникові рівняння; формувати вміння генерувати нові ідеї, ухвалювати оптимальні рішення, розвивати логічне мислення, увагу, творчий підхід до розв’язання рівнянь, сприяти самовихованню свідомого ставлення до навчання.

Обладнання: роздатковий матеріал: картки із завданнями.

Хід уроку.

Задача на розвиток логічного мислення для створення ситуації успіху.

На безлюдному острові ростуть три дерева – дуб, береза і сосна. Під кожним з них закопано скриню, в одній – тема уроку. На деревах – таблички:

 

 

 

 

Із трьох надписів – два правильні, один – помилковий. Дізнайтеся в якій скрині тема уроку?

Сьогодні ми повторимо тему: « Показникові рівняння», пригадаємо основні способи розв’язування показникових рівнянь. Наш урок- це урок повторення знань, а мета кожного такого уроку – підготовка до ЗНО.

1. Актуалізація опорних знань

Використовується метод   «незакінченого речення».

1. Показниковою  називається функція…
2. Область визначення показникової функції…
3. Область значень показникової функції…
4. Рівняння немає коренів коли…
5. Рівняння виду  Aa^2x+ Ba^x +C=0 розв’язується…
6. Рівняння 2^x=x+2   розв’язується….

 

Усне розв’язування рівнянь

3^x=                    (x=-2);

2^x=                    (x=-3);

9^x=27                   (x=1,5);

6^x=6                     (x=1);

8^x=1                     (x=0);

5^x=625                 (x=4).

Робота з таблицею: « Основні способи розв’язування показникових рівнянь.»       ( учитель роздає на кожну парту)

Способи розв’язування		Приклади
1 .       2.   3.     4.	Зведення до однакової основи   Винесення спільного    множника за дужки   Введення нової змінної     Графічний	2x = 45;   5x+1 + 5x = 150; 2x+2 - 2x = 96.   72x – 6 · 7x+5=0; 4x + 2x = 72;   2x = 0,8; 0,5x = 2x.

 

2. Розв’язування показникових рівнянь.

       Використовується інтерактивний метод «Акваріум». Клас об’єднується в чотири групи. Кожна група отримує завдання. Одна з груп сідає в центрі класу, утворивши внутрішнє коло. Усі учасники цієї групи починають обговорювати завдання. Усі інші учні мовчки спостерігають за обговоренням.

       Групі, що працює, необхідно  протягом 5хв. записати отримане завдання на дошці, обговорити хід розв’язування рівняння, розв’язати рівняння, записати розв’язання на дошці.

 Після закінчення часу група займає свої місця, а вчитель ставить класу запитання: «Чи правильно розв’язано рівняння?».

 Потім місце в «Акваріумі» займає інша група, яка отримує наступне завдання. Усі групи по черзі мають побувати в «Акваріумі» і результати роботи кожної з них слід обговорити в класі.

Завдання для першої групи

Розв’язати рівняння

9^{x + 0,5} + 26 · 3^x = 9.

Розв’язання

Зведемо степені, які є в рівнянні, до основи 3.

(3²)^{x + 0,5} + 26 · 3^x = 9;

3^{2x + 1} +  26 · 3^x - 9 = 0;

3^2x · 3 + 26 · 3^x – 9 = 0;

3 · (3^x)² + 26 ·3^x - 9= 0;

Зробивши заміну 3^х = у, отримаємо рівняння:

3у² + 26у – 9 = 0;

D = 784,

y₁ = -9;

y₂ = 1/3.

3^x = -9

Рівняння коренів не має.

3^x = 1/3;

3^x = 3^-1;

х = -1.

Відповідь: -1.

Завдання для другої групи

Розв’язати рівняння

6^x - 2^x · 3^{x + 1} + 72 = 0.

Розв’язання

Перейдемо до рівняння, яке містить 6^х, і виконаємо перетворення:

6^x -2^x · 3^x · 3 + 72 = 0;

6^x – 3 · 6^x + 72 = 0;

6^x ·(1 – 3) + 72 = 0;

6^x · (-2) = -72;

6^x = 36;

6^x = 6²;

х = 2.

Відповідь: 2.

Завдання для третьої групи

Розв’язати рівняння

 

Розв’язання

Оскільки   , то перейдемо до рівняння, яке містить лише степінь з основою.

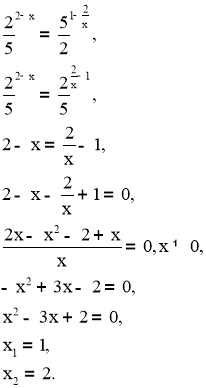
Відповідь: 1;2.

Завдання для четвертої групи

Розв’язати рівняння

3^{x + 3} + 3^{x + 4} + 3^{x + 5}= 13 · 9^x.

Розв’язання.

Перейдемо до рівняння , яке містить степені з основою 3, і здійснимо перетворення:

3^x · 3³ + 3^x · 3⁴ + 3^x · 3⁵ = 13 · ( 3² )^x;

3^x (3³ + 3⁴ + 3⁵ ) = 13 · 3^2x;

3^x · 351 = 13 · 3^2x;

27 · 3^x = 3^2x;

3³ · 3^x = 3^2x;

3^x+3 = 3^2x;

х + 3 = 2x²;

2x² - x - 3 = 0;

D = 1 + 24 = 25;

Відповідь:

 

ІІІ. Колективне розв’язування вправ

1. Розв’язати рівняння:

2^x + 2^2-x = 5.

 

Розв’язання.

Перейдемо до рівняння , яке містить степінь 2^х:

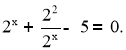
Зробимо заміну 2^х = у, отримаємо рівняння

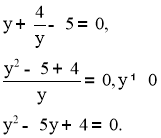
За теоремою, оберненою до теореми Вієта маємо:

у₁=4, у₂=1.

2^х=4,        2^х=1,

                                                         2^х=2²,      х₂=0.

х₁=2.

Відповідь: 0; 2.

2. Розв’язати рівняння:

Розв’язання.

 

Оскільки 8 = 2³, а 4 = 2², то перейдемо до рівняння, яке містить степінь з основою 2:

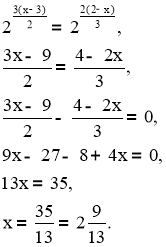
Відповідь: .

Виконання тестових завдань.( Збірник тестових завдань ЗНО 2006-20017. За матеріалами з досвіду роботи обласної компенсаційної школи вчителів математики Вінницької області)

Кожен отримує завдання. Після виконання учні здійснюють взаємоперевірку.

1. Якому з наведених проміжків належить корінь рівняння 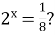( 2010)

А	Б	В	Г	Д
( - 6; - 4]	( -4; -2]	( -2; 0]	( 0; 2]	( 2; 4]

 

2. Якому з наведених проміжків належить корінь рівняння 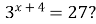(2010)

А	Б	В	Г	Д
[ - 4; - 2)	[ -2; 0)	[ 0; 2)	[ 2; 4)	[ 4; 6)

 

3. Розв’яжіть рівняння 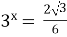. (2008)

А	Б	В	Г	Д
Рівняння не має коренів	-1	-0,5	0,5	1

 

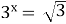
4. Якщо  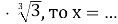 (2007)

А	Б	В	Г	Д
				3

 

5. Укажіть суму коренів рівняння 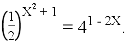(2008)

А	Б	В	Г	Д
-4	-2	2	4	5

 

6. Розв’яжіть рівняння 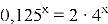(2003)

А	Б	В	Г	Д
		-1	-2

 

7. Укажіть проміжок, якому належить корінь рівняння 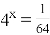. (2009)

А	Б	В	Г	Д
[-4;-1)	[2;5]	( -18; -4)	[ 0; 2)	[-1; 0)

 

8. Укажіть, якому з наведених проміжків належить корінь рівняння 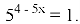(2008)

А	Б	В	Г	Д
( - 3; - 2)	( 0; 1)	( 1; 2)	( -1; 0)	( 2; 3)

 

4. Застосування показникової функції.

Багато процесів у природі і техніці можна описати формулою показникової функції: кількість бактерій зростає по експоненті, сила струму спадає по експоненті, приріст капіталу в банку змінюється за властивістю показникової функції.

Задача. Визначити кількість населення світу у 2018 році, якщо у 2010 році на землі проживало 7 млрд. осіб. Середньорічний приріст населення становить 2%.

Розв’язання

 

Для обчислення скористаємося формулою складних відсотків:

 

де A- шукана величина,

A₀- відома кількість населення,

P- середньорічний приріст населення у відсотках,

t- розрахунковий термін, t = 2018 - 2010=8 (років).

Врахувавши відомі дані, отримаємо:

A=7·(1+0,02)⁸=7·1,02⁸≈8(млрд. осіб).

Відповідь: ≈8млрд. осіб.

5. Підсумок уроку.
6. Домашнє завдання.

Розв’язати рівняння

36^x – 4 · 6^x – 12 = 0;

2^x+2 - 2^x = 96;

4^x+1 + 4^x = 320.