Методика навчання учнів розв’язуванню прикладних задач методом рівнянь

 

План

1. Розв’язування прикладних задач в курсі алгебри 7 класу

2. Навчання восьмикласників розв’язування прикладних задач методом рівнянь

3. Дробово-раціональні рівняння як моделі прикладних задач

4. Апробація основних результатів дослідження

Висновки

Список використаних джерел

 

 

1. Розв’язування прикладних задач в курсі алгебри 7 класу

Традиційно розв’язування різних задач вважалось і предметом навчання математики, і ефективним засобом формування математичних знань і вмінь, розвитку інтелекту та виховання учнів. Тому текстові задачі вивчаються у курсі шкільної математики від першого дня до випускного класу. Спочатку за їх допомогою розкривають смисл арифметичних дій над числами та властивості цих дій. А згодом їх використовують для закріплення теоретичних знань під час розв’язування прикладних і практичних задач.

За час навчання у школі учні розв’язують значну кількість прикладних задач, проте розв’язування таких задач залишається для них складним. Основна причина недостатньої сформованості в учнів умінь розв’язувати текстові задачі полягає у тому, що під час навчання математики як у початковій, так і в основній школах переважна більшість учнів не одержує достатніх знань про структуру задач, їх типи, методи та способи розв’язування. Розв’язуючи задачі, учні часто діють несвідомо, за зразком, що їм пропонують, не можуть самостійно знайти раціональний спосіб розв’язування. Серед інших причин такого стану – неправомірне зменшення використання арифметичних способів під час розв’язування текстових задач в основній школі та передчасний перехід до використання методу рівнянь.

Нині ситуація змінюється. Розгляд арифметичних способів розв’язування прикладних задач передбачено програмою з математики для основної школи та підпорядковано таким цілям:

1) формування загального підходу, загальних умінь і здібностей із розв’язування будь-яких задач (зокрема і методом рівнянь);

2) ознайомлення та свідоме оволодіння математичними і загальнонауковими поняттями;

3) оволодіння поняттями «модель» і «математичне моделювання», ознайомлення із застосуванням математичного апарату до розв’язування задач прикладного та практичного змісту;

4) розвиток розумових здібностей учнів, їх творчого потенціалу.

Зауважимо, що задачі в шкільній математиці існують не ізольовано від решти навчального матеріалу, їх зміст узгоджується з програмовим теоретичним матеріалом, що вивчався та буде вивчатися. За програмою з математики для основної школи передбачено, що у 5-му класі – аналіз залежностей між величинами (швидкість, час і відстань; ціна, кількість і вартість тощо) і розв’язування нескладних текстових задач (дещо прикладного характеру) на основі використання цих залежностей; розв’язування задач розрахункового характеру на основі використання властивостей арифметичних дій, задач на знаходження дробу від числа і числа за його дробом, відсотків від числа та числа за його відсотками; розв’язування задач прикладного змісту з використання правила знаходження середнього арифметичного кількох чисел. У 6-му класі: розв’язування задач на дії з дробами; розв’язування трьох основних задач на відсотки, задач на пропорційні величини і пропорційний поділ.

У книжці Лук’янової С. «Розв’язування текстових задач арифметичним способом: 5-6 класи» ви можете розглянути різні арифметичні способи розв’язування текстових задач та оригінальні методики навчання цього учнів 5-6 класів. Автор розглядає близько 200 задач різних рівнів складності. До більшості з них запропоновано розв’язання (до деяких – кількома способами), кожне з яких реалізується тільки за допомогою арифметичних дій.

Шкільна практика свідчить, що хоча метод рівнянь розглядають уже в 6 класі та використовують упродовж всього подальшого вивчення шкільного курсу математики, результати вступних екзаменів до вищих навчальних закладів незаперечно доводять, що значна частина випускників слабко опанувала цей метод.

Однією з причин цього ми вважаємо недостатню увагу вчителів до розв’язування в 5-6 класах арифметичним способом текстових задач і вправ, які безпосередньо готують учнів до усвідомлення методу рівнянь. Крім того, потрібно спеціально контролювати засвоєння учнями евристичної схеми пошуку рівняння як моделі зв’язків між відомими і шуканими.

Уміння розв’язувати задачі методом рівнянь як компонента відповідної діяльності містить такі розумові дії: аналіз задачі (виокремлення умов і вимог); встановлення істотних зв’язків між відомими і шуканими; виявлення величин, значення яких прирівнюватимуться, позначення невідомої та подання потрібних величин через введену невідому, складання рівняння і його розв’язування; перевірка розв’язування задачі. Уміння можна сформувати, якщо попередньо відпрацьовано всі його складові.

Успішно аналізувати формулювання прикладної задачі учні можуть лише тоді, коли вони засвоїли її зміст. Для цього важливо вдало подати задачу учням. Це можна зробити по-різному. Якщо задача з підручника, то ефективніше, коли задачу вголос читає вчитель або один із учнів, а решта стежать, як сформульовано задачу. Досвід свідчить, що найкраще, коли задачу читають не менше як двічі. Доцільно, щоб учень, який розв’язуватиме задачу, після повторення змісту задачі та виокремлення умови і вимоги скорочено записав її на дошці. Перші скорочені записи на дошці вчителеві доцільно робити самому, пропонуючи зразок, що його наслідуватимуть учні. Для окремих задач умову і вимогу потрібно подати у вигляді таблиці або графічної ілюстрації. Наведемо приклад.

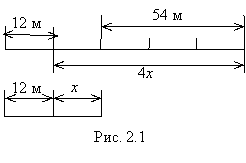
Задача 2.1. Один кусок дроту на 54 м довший за другий. Після того як від обох відрізали по 12 м, перший виявився в 4 рази довшим, ніж другий. Знайди довжину кожного куска.

Скорочений запис змісту задачі може мати вигляд:

 І ІІ + 54 -12;  ІІ*4   ?

 ІІ   -12    ?

Геометричне зображення змісту задачі наочно ілюструє зв’язок між даними і шуканими, допомагає доцільно вибрати невідому х і скласти просте для розв’язання рівняння 3х = 54 (рис. 2.1).

У процесі пошуку рівняння потрібно з’ясувати, про які величини йдеться в змісті задачі, які зв’язки існують між цими величинами і шуканими, значення яких величин можна прирівняти. Залежно від цього доцільно ввести невідому і скласти рівняння.

У методиці навчання алгебри відомі дві евристичні схеми пошуку рівняння до задачі. Першу схему застосовують до розв’язування нескладних задач, вона має такий вигляд: 1) позначити як х шукану величину (або одну із шуканих); 2) виразити через х інші величини, про які йдеться в змісті задачі; 3) ґрунтуючись на залежності між відомими і невідомими величинами, скласти рівняння.

Друга евристична схема зручна для розв’язування складніших задач: 1) з’ясувати, виходячи зі змісту задачі, значення яких величин можна прирівняти; 2) вибрати невідому і позначити її буквою х; 3) виразити через х значення величин, які прирівнюватимуться; 4) скласти рівняння.

Друга евристична схема забезпечує цілеспрямований вибір невідомої та вираження через неї потрібних величин. [19]

На першому підготовчому етапі навчання учнів методу рівнянь потрібно нагадати всі види основних задач, які розв’язуються кожною арифметичною дією, їх буквений запис, сформувати навички складання простих виразів з невідомою. Далі розв’язуються усно найпростіші задачі на складання рівнянь за умовою задачі. Для прикладу наведемо кілька задач.

1. До якого числа слід додати 12, щоб отримати 68? (Учні позначають як х невідоме число і записують рівняння: х + 12 = 68.)
2. Число a на 7 більше за  число b. Як можна записати залежність між a і b за допомогою рівності?
3. Число m втричі більше за число п. Як можна записати залежність між m і п за допомогою рівності?
4. Купили 10 кг цукерок по х гривень за 1 кг. Як записати у вигляді виразу вартість покупки?

Найбільшої уваги потребує подання в алгебраїчній формі величини, що знаходиться у даному різницевому або кратному відношенні з другою величиною.

Частина учнів ще і в 7-му класі відчуває труднощі при переведенні на мову алгебри залежностей «на стільки - то більше, менше», «у стільки-то разів більше, менше». З цими учнями необхідно додатково розв'язувати вправи такого, наприклад, змісту:

1. Число х більше від числа 7 на 3. Складіть рівність.

(х—7 = 3; х— 3 = 7; х = 7 + 3).

2. Складіть рівність, якщо а більше від 5 у 4 рази.

3. Сума двох чисел дорівнює 15. Одне з них а. Запишіть друге число.

4. Дано числа х і у. На скільки перше число більше за друге? Друге більше від першого?

5. В одному кошику с яблук, у другому у 2 рази, а в третьому у 4 рази більше, ніж у першому. Скільки яблук у другому кошику, у третьому, у трьох кошиках разом?

6. У п'ятому класі х учнів; у шостому на 3 учні більше, ніж у п'ятому, а в сьомому на 2 учні менше, ніж у шостому. Скільки учнів у сьомому класі?

7. На верхній полиці лежить т книжок, на середній удвоє, а на нижній утроє більше, ніж на верхній. Скільки книжок на усіх трьох полицях?

8. В одному кошику х груш, у другому на 12 груш більше, а в третьому на 25 груш більше, ніж у другому. Скільки груш у всіх трьох кошиках?

Використання подібних вправ для роботи на уроках залежить від рівня підготовки класу в цілому і наявності в ньому учнів, у знаннях яких є істотні прогалини. Відповідно організується фронтальна робота з класом, групова або індивідуальна робота. В окремих випадках виникає необхідність розгляду вправ пропедевтичного характеру в спеціально відведений час на початку або в кінці уроку поза зв'язком їх з основною темою. Найбільший ефект дає диференційована індивідуальна допомога учням, що відчувають труднощі в оволодінні програмним матеріалом. [19]

У 7 - му класі значну питому вагу мають задачі, зміст яких переважно полягає в тому, що даються дві нерівні однорідні величини, які підлягають певним змінам. Складаючи вирази на основі залежностей, даних в умові, учні повинні подати алгебраїчною мовою зміни, яких зазнавали дані величини.

Підготовчими тут можуть бути вправи такого змісту:

1. У двох паралельних класах по х учнів. З одного класу перевели в другий двох учнів. Скільки учнів стало в кожному класі?

2. В одному ящику 20 кг гвіздків, а в другому 30 кг. Скільки кілограмів гвіздків буде в кожному ящику, якщо з другого перекласти в перший х кг?

3. В одній пачці а зошитів, у другій у 2 рази більше. Скільки зошитів буде в кожній пачці, якщо з більшої перекласти в меншу 10 зошитів?

Підготовчі вправи, спрямовані на актуалізацію необхідних знань, мають бути максимально наближені до змісту задач, які розв'язуватимуться в певному розділі.

Розглянемо це питання стосовно до прикладних задач з відсотковими розрахунками і відповідно задач з використанням запису числа у вигляді суми розрядних доданків та деяких інших.

Треба нагадати учням, що відсоток - це одна сота частина. Якщо якусь величину позначено через х, то один її відсоток становить 0,01 х, 25 % становлять 0,25х, 130 % — відповідно 1,3х і т. п. Якщо число а збільшили на 45 %, то це записують як 1,45а, якщо число в зменшили на 18 %, то воно становить 0,82 свого попереднього значення, тобто дорівнює 0,82в. Цей останній випадок потребує особливої уваги, бо учні іноді неправильно визначають основне число в задачах з «нарощеним числом».

Проаналізуємо цей помилковий підхід на прикладі задачі, розв'язаної складанням системи двох лінійних рівнянь. [5].

Задача 2.2 Токар і його учень повинні були виготовити за зміну 90 деталей. Завдяки тому, що токар перевиконав план на 20 %, а учень на 10%, вони виготовили 105 деталей. Скільки деталей виготовляли токар і його учень щодня?

Діючи за шаблоном, деякі учні вибирають за невідомі кількості деталей, які треба знайти, тобто

х — кількість деталей, що їх щоденно виготовляв токар, відповідно

у — кількість деталей, що їх щоденно виготовляв учень.

Далі міркують так: після підвищення продуктивності праці токар став виготовляти щоденно х деталей, отже, спочатку він виготовляв їх на 20 % менше, тобто 0,8х, а учень відповідно 0,9у.

Розв'язуючи систему рівнянь

дістають х = 45, у = 60. Цей розв'язок суперечить здоровому глузду. Правильне розв'язання задачі дістанемо тоді, коли за основні невідомі вибрати «ненарощені числа», тобто кількості деталей, які виготовляв токар і його учень до підвищення продуктивності праці. Розв'язуючи систему рівнянь

дістанемо х = 60, у = 30, тобто х + у=90. Після підвищення продуктивності праці маємо: 1,2х = 72; 1,1у = 33, тобто 1,2х + 1,1у = 105. [3, 20].

Під час розв'язування задач доводиться виконувати допоміжні відсоткові розрахунки з відомими числами: знаходити кілька відсотків від числа, число за його відсотками, обчислювати відсоткове відношення двох чисел. Усі такі розрахунки треба проводити, подаючи відсотки у вигляді дробів.

Розв'язуючи задачі з відсотками в класі або задаючи їх учням для домашньої роботи, учитель повинен щоразу думати про допомогу, яку треба надати учням (вказівку, застереження), щоб запобігти зайвих ускладнень і помилок.

Вміщені в кожному розділі задачі мають узгоджуватися з тими теоретичними відомостями, які вивчаються в певний час. Ці вимоги в основному додержані в діючих підручниках, проте труднощі, які відчувають учні під час самостійного розв'язування задач методом рівнянь, переконують в необхідності спеціальної роботи над деякими типовими залежностями, що фігурують в задачах.

Розглянемо для прикладу так звані задачі на рух. Цим задачам відведено значне місце в 3—6-х класах, і учні набувають певного досвіду в їх розв'язуванні.

У підручниках 7—9-х класів задачі на рух представлені у всіх розділах, пов'язаних з розглядом рівнянь, нерівностей та їх систем. Завдання вчителя полягає в тому, щоб озброїти учнів міцними навичками в складанні математичних виразів для залежностей, типових для задач на зустрічний рух, рух у протилежних напрямках і в одному напрямку. Особливої уваги потребує розв'язування задач на рух за допомогою раціональних рівнянь у 8-му класі, бо ці задачі викликають в учнів труднощі. Вкажемо на необхідність певної підготовчої роботи до розв'язування задач на рух, де використовуються поняття «рух за течією», «рух проти течії», «швидкість човна у стоячій воді», «власна швидкість теплохода» тощо.

Учні, спираючись на власний життєвий досвід, без труднощів усвідомлюють відповідні залежності, але їх треба своєчасно розглянути.

Розв'язуючи задачі на рух за допомогою рівнянь у 5—6-х класах, учні набули певного досвіду встановлення залежностей між даними і шуканими величинами в таких задачах. І все ж розв'язування дещо ускладнених задач на рух у курсі алгебри викликає в частини учнів значні труднощі. Тут можуть допомогти настанови, що розкривають ці залежності в загальному вигляді. Слід підкреслити учням, що, формулюючи ці закономірності, ми маємо на увазі «ідеальні умови», за яких здійснюється рух: швидкості рухомих тіл сталі на всьому проміжку шляху, тобто їх рух рівномірний, рух відбувається по прямій, зустріч відбувається в точці тощо. [3; 5; 22].

Слід обов’язково обговорювати з учнями ситуації в текстових задачах підручників, оскільки такі задачі є не зовсім прикладними, вони дещо ідеалізовані. Зробимо ще одне дуже важливе зауваження. Само по собі рівняння, складене за умовою задачі, не є повною математичною моделлю реальної ситуації, відображеної в умові задачі. Воно не враховує фізичні властивості предметів і явищ, про які йдеться в задачі, реальних співвідношень між допустимими значеннями відповідних фізичних величин. Тому розв'язки рівняння можуть не відповідати дійсності, і треба обов'язково перевірити, чи задовольняють корені рівняння умову задачі, чи враховують змістовні обмеження для значень розглядуваних величин. Отже, відповідь, що дістали за складеним рівнянням, необхідно перевірити за змістом задачі. Для цього досить при значенні невідомого, яке дорівнює кореню рівняння, обчислити по черзі значення величин, що входять у задачу. Якщо значення якоїсь величини виходить за межі допустимого за змістом задачі, то випробуваний корінь не може бути розв'язком задачі. Щоб корінь рівняння був розв'язком задачі, він має задовольняти всім змістовним обмеженням величин, введених у задачу (явно чи неявно).

Треба пояснити учням, що в багатьох випадках основне невідоме можна вибирати кількома способами.

Для зміцнення навичок подання допоміжних невідомих через основне невідоме доцільно продовжити тренування учнів у встановленні двобічних зв'язків між величинами, що фігурують в умові задачі: якщо одна величина більша від другої на якесь число (у кілька разів), то друга — менша від першої на це саме число (у стільки ж разів).

З цією метою треба використовувати задачі з підручника. Наприклад, учитель пропонує перефразувати задачу так, щоб замість слова «більше» вживалося слово «менше», а зміст задачі не змінювався. [3].

Задача 2.3 У трьох цехах заводу працює 1274 робітники. У першому цеху на 70 робітників менше, ніж у другому, а в другому — на 84 робітники менше, ніж у третьому. Скільки робітників працює в кожному цеху?

Позначивши через х число робітників у другому цеху, дістанемо рівняння:

х + (х – 70) + (х + 84) =1274,

х + х – 70 + х + 84 = 1274,

3х + 14 = 1274,

3х = 1260

х = 420.

Доцільно дати учням домашнє завдання за варіантами відносно вибору основного невідомого. Наприклад, за х позначити число робітників другого цеху, а іншому варіанту – число робітників третього цеху.

Завдання перевіряється за заздалегідь підготовленою вчителем таблицею, яку після розбору учні записують у зошити.

 

І	х	х – 70	х – 84 – 70
ІІ	х + 70	х	х – 84
ІІІ	х + 70 + 84	х + 84	х

 

Записуються також відповідні рівняння.

Далі з'ясовується питання, яке ж невідоме доцільніше вибрати за основне. Мабуть, учні скажуть, що через х доцільно було позначити кількість робітників ІІ цеху.

Учитель підкреслює, що під час розв'язування задач на поділ числа на нерівні частини у різницевому чи в кратному відношеннях для зручності беруть за основне невідоме найменшу величину (якщо це можливо). Проте це необов'язково.

Дехто може заперечити, що такий докладний аналіз однієї, до того ж нескладної, задачі зайвий. Це хибна думка. Спостереження показують, що типовим недоліком при введенні методу рівнянь для розв'язування задач є поспішність, ігнорування того факту, що частина учнів не усвідомлює матеріалу на належному рівні. Розв'язання однієї задачі кількома способами буває значно корисніше, ніж розв'язання одним способом кількох задач. Після розв'язання задачі кількома способами чи введення якихось нових елементів важливо підводити підсумок проведеної роботи, акцентувати увагу учнів на необхідність засвоєння тих прийомів, які будуть потрібні їм у наступній діяльності.

Задача 2.4 Навесні учні 7 класів прийняли участь в благодійній акції «Подаруй дерево місту». Школою було закуплено 76 саджанців, які потрібно було розподілити між трьома класами. У 7-А класі навчається у два рази менше учнів ніж у 7-Б, а у 7-В на 12 учнів більше ніж у 7-А. Скільки саджанців потрібно виділити кожному класу?

Розв’язання задачі

Нехай першому класу потрібно виділити х саджанців. Тоді другому слід виділити 2х саджанців, а третьому (х+12) саджанців.

Загальна кількість саджанців х + 2х + (х + 12), що за умовою задачі дорівнює 76.

Отже, х + 2х + (х + 12) = 76.

Розв’яжемо це рівняння:

х + 2х + х + 12 = 76,

4х = 76 – 12,

4х = 64,

х = 16.

Отже, 7-А потрібно віддати для посадки 16 саджанців, 7-Б – 32 (2∙16=32) саджанці, а 7-В – 28 саджанців, оскільки учнів в цьому класі на 12 більше ніж в 7-А (16+12=28).

Відповідь. 7-А – 16 саджанців, 7-Б – 32 саджанці, 7-В – 28 саджанців.

  Доцільно було б розв’язати задачу змінивши загальну кількість саджанців, наприклад на 78, учні за аналогією швидко складуть рівняння і розв’язавши його (х = 16,5) прийдуть до протиріччя: Як можна поділити саджанці так, щоб 7-А дісталося шістнадцять з половиною саджанців? Проаналізувавши ще раз умову задачі, приходимо до висновку – за змістом задачі х повинно бути натуральним числом, а отже, такий розподіл саджанців зазначеним способом ( кожному учню по одному саджанцю) неможливий.  

Розглянемо ще декілька цікавих задач, аналогічні яким доцільно розв’язати на уроках алгебри в 7-му класі під час вивчення теми «лінійні рівняння з однією змінною». А в додатку 1 представлена добірка прикладних задач для сьомого класу, які розв’язуються за допомогою систем лінійних рівнянь з двома змінними.

Задача 2.5  Для штукатурки зовнішньої поверхні будинку необхідно приготувати цементно-вапняний розчин марки 500 об’ємом 2,4 м³. скільки необхідно цементу, вапняного тіста і піску, якщо їх об’ємне відношення відповідно дорівнює 1 : 2 : 9?

Розв’язання задачі

За умовою задачі відношення об’ємів цементу, вапняного тіста і піску в цементно-вапняному розчині марки 500 становить, відповідно, 1 : 2 : 9. Введемо коефіцієнт пропорційності х. Тоді 2,4 м³ цього розчину містить х м³ цементу, 2х м³ вапняного тіста і 9х м³ піску. Маємо рівняння:

х + 2х + 9х = 2,4.

Після спрощення останнього рівняння приходимо до лінійного рівняння з однією змінною 12х = 2,4. корінь якого х = 0,2. Цементно-вапняний розчин містить:

х = 0,2м³ цементу;

2х = 2 ∙ 0,2 = 0,4м³ вапняного тіста;

9х = 9 ∙ 0,2 = 1,8м³ піску.

Сума об’ємів компонентів цементно-вапняного розчину дорівнює об’єму всього розчину, тобто:

0,2 + 0,4 + 1,8 = 2,4;

Відношення об’ємів компонентів цього розчину 0,2 : 0,4 : 1,8 = 1 : 2 : 9.

Відповідь. 0,2 м³; 0,4 м³; 1,8 м³.

Задача 2.6 При розмелюванні пшениці отримують 90 % борошна, а при випіканні хліба виходить 40 % припічки (різниці між масою хліба та необхідною для його випікання масою борошна). Скільки гектарів поля потрібно засіяти пшеницею, щоб випекти 7 тонн хліба? Середня урожайність пшениці з гектара 35 ц.

Розв’язання задачі

Нехай потрібно засіяти пшеницею х гектарів поля. Оскільки середня урожайність пшениці дорівнює 35 ц, то з усього поля зберуть 35х ц пшениці. При розмелюванні пшениці отримують 90 % борошна, тому з 35х ц пшениці можна отримати 35х ∙ 0,9 = 31,5х ц борошна. Маса хліба перевищує необхідну масу борошна на 40 %, тому маса хліба з 31,5х ц борошна дорівнює 31,5х  ∙ 1,4 = 44,1х ц. Маємо лінійне рівняння 44,1х = 70 (7 тонн = 70ц), х 1,59. Отже, щоб випекти 7 т хліба, необхідно засіяти пшеницею 1,59 га поля.

Відповідь. 1,59 га.

Задача 2.7 Один робітник виконує деяку роботу за т днів, а другий робітник ту саму роботу може виконати за п днів. За скільки днів виконають цю роботу обидва робітники, працюючи разом?

Розв’язання задачі

Обсяг усієї роботи позначимо за одиницю. Тоді продуктивність праці першого робітника за 1 день становитиме 1/т, другого – 1/п. Позначимо невідому кількість днів спільної роботи через х, тобто за х днів робітники виконають усю роботу. Маємо рівняння:

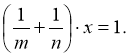
Отримане рівняння зводиться до лінійного з однією змінною:

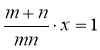
( - дійсне число, що знаходиться за умовою задачі).

Його розв’язок  Працюючи спільно, обидва робітники виконають роботу за   днів.

Відповідь.   днів.

Задача 2.8  Скільки треба взяти води при 5°С і води при 40°С, щоб отримати 15 кг суміші при 19°С?

Розв’язання задачі

Нехай потрібно взяти х кілограмів води при 5°. Тоді решта (15 – х) кг – це вода з температурою 40°. При змішуванні води з різною температурою відбувається процес теплообміну: вода з меншою температурою 5°, нагріваючись до 19°, поглинаю деяку кількість теплоти Q₁, а вода з вищою температурою 40 °, охолоджується до 19 °, віддає деяку кількість теплоти Q₂. Якщо вплив навколишнього середовища на процеси, що розглядаються, незначний, то можна наближено вважати, що Q₁ = Q₂.

З курсу фізики відомо, що кількість теплоти, надана тілу внаслідок його нагрівання або виділена ним під час охолодження, залежить від маси тіла т, роду речовини с та зміни температури тіла ∆t: Q = ст∆t. Коефіцієнт пропорційності с називається питома теплоємність речовини. Керуючись цими відомостями, визначимо Q₁ та Q₂:

Q₁ = сх(19 – 5) = 14сх,

Q₂ = с(15 – х)(40 – 19) = 21с(15 – х),

де с – питома теплоємність води. Покладаючи Q₁ = Q₂, отримаємо рівняння 14сх = 21с(15 – х). Спрощуючи останнє рівняння, приходимо до лінійного рівняння 35х = 315, розв’язок якого х = 9.

Отже, щоб отримати 15 кг води при 19° потрібно взяти 9 кг води при 5° і 15 – х = 15 – 9 = 6 (кг) води при 40°.

Відповідь. 9 кг, 6 кг.

Задача 2.9 З грядки зібрали кошик огірків. Скільки кілограмів огірків було в кошику, якщо 4/5 їхньої маси розклали в банки різної ємності: 2 трилітрові, 3 дволітрові та 3 літрові? Співвідношення маси огірків до об’єму банки, яку вони наповнюють, складає 2 : 3.

Розв’язання задачі

Нехай х – маса зібраних огірків. У банках міститься 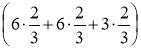кг огірків, що складає 4/5 їх початкової маси. Маємо рівняння:

Останнє рівняння після спрощення набуде вигляду х = 10. Звідки

х = 12,5.

Таким чином, у кошику було 12,5 кілограмів огірків.

Відповідь. 12,5 кг.

Кожна із запропонованих задач [8] може стати основою для створення багатьох інших прикладних задач із різним змістовим наповненням та фабулою, але спільною математичною структурою та ідеєю розв’язання.

2. Навчання восьмикласників розв’язування прикладних задач методом рівнянь

Майже всі учні середньої школи вважають, що якщо запропонована їм математична задача розв’язана правильно, якщо отримана відповідь співпадає з відповіддю, поданою в підручнику, або схвалена вчителем, то робота завершена та про розв’язання задачі можна і потрібно забути.

Таким чином, учні (а також і багато вчителів) забувають про навчальний характер кожної задачі, що розв’язується в процесі навчання, про те, що всяка задача повинна вчити їх вмінню орієнтуватися в різних проблемних  ситуаціях, збагачуючи їх знаннями та досвідом, вчить їх математичної діяльності.

Очевидно, що в процесі розв’язування задач учні накопичують певні відомості, що стосуються певних проблемних ситуацій або способів розв’язання. Але для ефективної роботи над розв’язанням нової прикладної задачі, в нових умовах необхідно, щоб отриманий раніше досвід був впорядкований. Необхідно, щоб різного роду інформація, отримана учнями в процесі розв’язування задачі, критично ними оцінювалася,  щоб підводились підсумки після кожної задачі. Отже, учнів слід навчити робити аналіз та підсумки до розв’язаної прикладної задачі.

Важливо помітити, що така діяльність виступає як одна із характеристик повноцінного мислення. Так, відомий психолог С. Л. Рубінштейн пише, що мислення – це актуалізація і застосування знань, що є одним процесом. Під процесом актуалізації розуміють відбір з минулого досвіду потрібних відомостей та методів і використання їх в нових умовах.

Англійський кібернетик Д. М. Маккей встановив чотири основні якості, що відрізняють «інтелект від простої здатності розв’язувати»:

1) здатність успішно обробляти та об’єднувати інформацію в залежності від її значущості;

2) здатність виконувати пробні дії, пошук і переходи, що не випливають із поданої інформації (тобто виконувати «стрибок через розрив, існуючий в даних»);

3) здатність керувати пошуковим і дослідницьким процесом, управляти «відчуттям близькості розв’язку»;

4) здатність розглядати обмежений, але достатньо великий ряд положень та висновків, спільних з даним становищем.

Більшість задач поданих в підручниках для 8 класів шаблонні до завдань тренувального характеру. Д. Пойа справедливо відмітив: «Є задачі і задачі, і все можливі відмінності між ними. Але найбільш важлива для вчителя відмінність – це вміння розрізняти  шаблонні та нешаблонні задачі». Виділяючи два основні типи шаблонних задач – «задачі за одним правилом» і «словесні задачі», Д. Пойа говорив: «Шаблонні задачі, навіть тільки двох щойно описаних типів, можуть бути корисними або навіть необхідними, якщо вони дані в певний час та в потрібній мірі…»

Так наприклад, в першій темі третього розділу «Квадратні рівняння. Неповні квадратні рівняння, їх розв’язування» (8 клас) доцільно було б почати з розв’язування «шаблонних» задач, з заздалегідь вивченими методами, в наступних темах ввести простіші прикладні задачі, а вивчення розділу завершити більш складними та нешаблонними задачами (тобто використати метод «від простого до складного»).

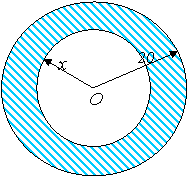Задача 2.10   Площа кільця дорівнює 942 см², а радіус його зовнішнього кола 20 см (мал. 2.2). Знайдіть радіус його внутрішнього кола.

Розв’язання задачі

Для початку потрібно пригадати формулу для обчислення площі круга – S = πr².

1) за даними задачі можна обчислити площу більшого круга:

S = π ∙ 20² = 400π = 400 ∙ 3,14 = 1256 (см²);

2) нехай радіус внутрішнього кола дорівнює х см, тоді площа внутрішнього круга – π х² см² або 3,14 х² см². А площа кільця дорівнює різниці площ зовнішнього та внутрішнього кругів. Отже, маємо рівняння:

1256 - 3,14 х² = 942,

3,14 х² = 1256 – 942,

3,14 х² = 314,

х² = 100,

х₁ = 10,  х₂ = -10.

3) аналіз отриманих результатів. х₂ = -10 – сторонній корінь, оскільки за х ми позначали радіус внутрішнього кола, то це значення не може бути від’ємним числом. Отже, радіус внутрішнього кола 10 см.

Відповідь. 10 см.

Задача 2.11 Лісосіка має 200 000 м³ деревини. Кількість деревини зростає щороку на однакову кількість відсотків, у результаті через два роки об’єм становив 212 180 м³. Визначити щорічний приріст деревини у відсотках.

Розв’язання задачі

Нехай х – щорічний приріст деревини (у відсотках), 200 000 м³ – початковий об’єм деревини. Тоді за перший рік у лісосіці об’єм деревини збільшиться на 200 000 х м³. Новий об’єм деревини, що знаходиться в лісосіці наприкінці першого року, становить 200 000 + 200 000 х м³. За другий рік об’єм деревини в лісосіці зросте на (200 000 + 200 000 х ) х м³. Об’єм деревини, яку містить лісосіка наприкінці другого року, становить 200 000 + 200 000 х + (200 000 + 200 000 х ) х м³. За умовою задачі цей об’єм дорівнює 212 180 м³, тобто

200 000 + 200 000 х + (200 000 + 200 000 х ) х = 212 180.

Отримане рівняння зводиться до квадратного: х² + 2х – 0,0609 = 0. Його корені х₁ = -2,03; х₂ = 0,3.

Корінь х₁ сторонній корінь (приріст деревини – додатна величина). Другий корінь х = 0,3 задовольняє умову задачі. Таким чином, щорічний приріст деревини у лісосіці дорівнює 0,3 або 30%.

Відповідь. 30%.

Задача 2.12 На прямокутній клумбі розміром 3 м × 4 м висаджено 36 кущів троянд (посадка рівномірна). На яку однакову величину треба змінити довжину та ширину клумби, щоб з такою самою щільністю посадити 90 кущів троянд?

Розв’язання задачі

З умови задачі безпосередньо визначаємо площу клумби:

S = 3 ∙ 4 = 12 (м²).

Тоді на один квадратний метр припадає 36 : 12 = 3 кущі троянд. Отже, густина троянд на новій ділянці дорівнює 3 кущі на 1 м².

Нехай довжину та ширину клумби збільшили на х метрів. Тоді площа нової клумби дорівнює (3 + х)(4 + х) м². Кількість троянд, яку можна посадити на новій ділянці, дорівнює 3(3 + х)(4 + х). За умовою задачі останній вираз дорівнює 90. Маємо рівняння:

3(3 + х)(4 + х) = 90.

Після спрощення отримаємо квадратне рівняння х² + 7х – 18 = 0, корені якого х₁ = -9, х₂ = 2.

Перший корінь сторонній (х – додатна величина). Другий корінь х = 2 задовольняє умову задачі. Отже, сторони клумби збільшити на 2 метри.

До недоліків в постановці задач, характерних для більшості підручників, можна віднести, наприклад, наступні:

1) завелика стандартизація змісту та методів розв’язання;

2) збільшення числа розв’язуваних школярами стандартних текстових задач за рахунок їх навчальної якості;

3) недосконалість методики навчання через задачі;

4) невідповідність постановки задач та їх розв’язків в школі закономірностям мислення, що розвивається;

5) захоплення розв’язуванням таких задач чи вправ, що в майбутньому майже не використовуються ні в процесі вивчення основних наук, ні на практиці;

6) навчання школярів через задачі таким вмінням та навичкам, які в сучасній практичній діяльності майже не використовуються, а в діяльності недалекого майбутнього будуть повністю замінені ІКТ;

7) відсутність чітких критеріїв навчального значення кожної задачі, поставленої в процесі навчання.

З метою ілюстрації сказаного зупинимось на розгляді кількох задач фінансово-економічного змісту, для яких рівняння є математичними моделями. Слід зазначити, що завдання підходять для спеціалізованих шкіл економічного напрямку.

Задача 2.13 Аналізуючи показники матеріаломісткості продукції, ставлять завдання: якою повинна бути валова продукція за звітний період, якщо перевитрати матеріалів складають 25 тис. грн. при відомих даних (табл. 1); який буде при цьому додатковий випуск продукції?

Таблиця 1.

Показники	Минулий період	Звітний період	Відхилення
1. Матеріальні витрати (тис. грн.)	1400	1550	1150
2. Валова продукція (тис. грн.)	1850
3. Матеріаломісткість валової продукції	0,757

 

Розв’язання задачі

Для визначення витрат чи економії матеріалів за рахунок зниження чи збільшення матеріаломісткості продуктів, зміну коефіцієнта матеріаломісткості множать на матеріальні витрати минулого періоду.

Позначимо матеріаломісткість за звітний період х, тоді зміна коефіцієнта буде (х – 0,757) і отримаємо рівняння:

1400 ∙ (х – 0,757) = 25,

х – 0,757 = 0,01785,

х = 0,77485,

х 0,775.

Тоді знаючи, що матеріаломісткість – це частка від ділення матеріальних витрат на валову продукцію (у), отримаємо інше рівняння: 1550 : у = 0,775. Його коренем буде число у = 2000.

Додатковий випуск продукції визначається шляхом множення перевитрат матеріалів на матеріаловіддачу минулого періоду або діленням на матеріаломісткість:

25 : 0,757 33,03 (тис. грн.)

Отже, перевитрати матеріалів складають 25 тис. грн. Це, в свою чергу, призвело до збільшення випуску продукції на 33,03 тис. грн.

Відповідь.  2 000; 33,03 тис. грн.

Як видно, такого типу задачі призводять до складання лінійних рівнянь, але їх розв’язання в 7-х класах було б недоцільне і цьому є декілька причин. Однією з них є міжпредметні зв’язки, а саме розв’язування лінійних рівнянь та вивчення економічних тем відповідного змісту.

Задача 2.14 За даними (табл. 2)

Таблиця 2.

Показники	Звітний рік		Відхилення
	план	факт
1. Середньоспискова чисельність персоналу (шт.)	170	174	+4
2. Обсяг продукції	20 000	20 500	+500

 

Розрахувати, яким повинен бути середньорічний виробіток, щоб кількісний фактор збільшив обсяг продукції  на 500 тис. грн., а якісний – на 30 тис. грн.

Якісний фактор, це: де φ – чисельність, В – середньорічний виробіток, тому можна скласти рівняння для вирішення цієї проблеми:

500 000 = (174 – 170) ∙ х.

Розв’язавши його, маємо: х = 125 000. Отже, В_пл. = 125 000. Якісний фактор – це: тоді маємо інше рівняння:

3 000 = (х – 125 000) ∙174.

Знаходимо його корінь: х - 125 00 = 3 000 : 174, тобто х = 124 827,6.

Отже, В_ф. = 124 827,6 грн.

Відповідь. Середньорічний виробіток фактично повинен складати 124 827,6 грн.

В додатку 2 можна ознайомитись із збіркою прикладних задач для 8 класу.

 

3.  Дробово-раціональні рівняння як моделі прикладних задач

 В програмі з математики для 5 – 12 класів сформульовані держані вимоги до рівня загальноосвітньої підготовки учнів, зокрема для учнів 9-х класів є такі вимоги:

- учень повинен наводити приклади математичних моделей реальних ситуацій;

- учень повинен розв’язувати вправи, що передбачають складання і розв’язування систем рівнянь з двома змінними як математичних моделей текстових задач.

Щоб досягти такої мети потрібно включати текстові задачі до кожної теми протягом всього навчання. В третьому розділі алгебри 9 класу «Елементи прикладної математики» за програмою передбачено виділення годин на вивчення математичного моделювання. При вивченні цієї теми розширюється уявлення учнів про математичні моделі реальних ситуацій. Розв’язування задач на цьому етапі навчання нерідко передбачає розв’язування дробово-раціональних рівнянь та їх систем.

Використання різних форм організації розв’язування задач сприяє кращому засвоєнню знань та виробленню вмінь та навичок. На уроці можливе колективне фронтальне розв’язування задач, колективна робота окремих груп і самостійне розв’язування, тощо. До підготовки кожного уроку слід підходити творче, враховувати особливості аудиторії, підбирати відповідні прикладні задачі, щоб зацікавлювати учнів. Так наприклад, для вихованців школи-інтернату можна запропонувати наступні задачі.

Задача 2.15 Учень 9 класу нашої школи, якому держава дає грошову допомогу як сироті, поклав до банку 3 000 гривень під 8 % річних. Яку суму він матиме на рахунку через рік?

Задача 2.16 Перебуваючи у літньому таборі праці та відпочинку, бригада старшокласників нашої школи із 15 чоловік одержала дві пропозиції. Перша – від сільськогосподарського кооперативу «Надзбруччя» - висадити розсаду помідорів на 0,8 га з подальшою оплатою 20 грн. на особу та 10 кг дозрілих помідорів. А друга пропозиція надійшла від місцевого лісгоспу, який запропонував очистити територію лісу від хмизу з оплатою 10 грн. на особу за очищення 0,04 га в день. Усього ліс займав 15 га. Рада старшокласників зібралася, щоб вирішити, на яку пропозицію вигідніше пристати? Школярі, розділившись порівну, зайняли у розв’язанні задачі діаметрально протилежні позиції.

Задача 2.17 Учениця 9 класу під час зимових канікул з дозволу матері працювала у фірмі, розповсюджуючи косметику. Керівництво фірми зобов’язувалось виплатити дівчині за кожні три продані комплекти по 10% від отриманої суми. Учениця розповсюдила за 10 днів 45 комплектів на суму 340 грн., за що отримала 25 грн. Яку судове рішення прийме клас на захист учениці?

Задача 2.18 Завідувач столярної майстерні одержав замовлення на виготовлення 60 кухонних дощок. Замовник пообіцяв за кожну виготовлену дошку заплатити по 17 грн. Але майстерні треба замовити шпон на фірмі з обробки деревини. За 1 м² шпону треба заплатити по 12 грн. Чи варто бригаді учнів столярів братися за виконання цього замовлення?

На нашу думку задачі такого типу на уроках математики сформують у вихованців творче ставлення до будь-яких форм діяльності, залучить їх до реальних виробничих відносин і форм, зорієнтованих  на особливості ринкової системи, економічного мислення, а головне – викличуть потребу в праці.

Для  спеціалізованих шкіл, або ліцеїв з поглибленим вивченням економіки такі прикладні задачі були б не доцільними, оскільки зацікавленість в таких учнів зосереджена на задачах іншого типу. Задачі економічного змісту – це задачі, які стосуються фінансів, побуту, торгівлі, грошових розрахунків, вибору оптимального рішення тощо.

Розглянемо фінансово-економічну задачу для учнів економічного ліцею.

Задача 2.19 Маючи економічну залежність між ціною на товар Р і величиною попиту де а₀, а₁, а₂ – числа), визначити, при якій ціні прибуток F, буде 13,27 у.г.о., якщо сталі витрати С = 10 у.г.о., а витрати пропорційні обсягу виробництва VD – 2у.г.о.? Обчислені для певного виду товару коефіцієнти відповідно рівні: а₀ = 8,58, а₁ = 0,78, а₂=0,01.

Розв’язання задачі

Відомо, що для знаходження прибутку потрібно від товарообігу в грошовому вимірі Z відняти всі затрати:

F = Р ∙

Для даного прикладу:

Z = 8,58 – 0,78х + 0,01х², тому 25,27 = 8,58х – 0,78х² + 0,01х³, де х – ціна.

Одержане рівняння рівносильне рівнянню:

х³ – 78 х² + 858 х – 2527 = 0.

Розкладемо його на множники:

(х³ - 343) – 78(х² - 11х  + 28) = 0,

(х – 7)( х² + 7х  + 49) – 78(х - 7)( х - 4) = 0,

(х – 7)( х² + 7х  + 49 – 78х + 312) = 0,

(х – 7)( х² - 71х  + 361) = 0.

Це рівносильно:

а) х – 7 = 0 –лінійне. Звідси х = 7.

або

б) х² - 71х  + 361 = 0 – квадратне. Знаходимо його корені.

D = 5041 – 1444 = 359760².

х₁ = 65,5; х₂ = 5,5.

Отже, можна зробити висновок, що прибуток буде однаковий, якщо встановити ціни 5,5 у.г.о., 7 у.г.о., 65,5 у.г.о. Зрозуміло, що при цьому попит на товар буде різний. Найменшим він буде при найбільшій ціні 65,5 у.г.о. Тоді D = 8,58 – 51,09 + 42,9 = 0,39 (практично мінімальний). Тому таку ціну встановлювати не бажано. При 5,5 у.г.о. – товарообіг 4,3 у.г.о., при ціні 7у.г.о. – товарообіг 3,61 у.г.о. Отже, найкращий товарообіг при ціні 5,5 у.г.о.

Відповідь. 5,5 у.г.о.

Для вирішення цієї проблеми було складено рівняння третього степеня. Запропонований метод його розв’язання не є очевидним і простим. Виникає проблема розв’язання такого типу рівнянь. Існують інші економічні завдання, які приводять до складання і розв’язання довільних рінянь. Тому математиками було досліджено і відпрацьовано довільні рівняння і прийоми їх розв’язування та складено класифікацію рівнянь із запропонованими методами їх розв’язування. Розглянемо ще декілька задач не економічного змісту, які більш підходять для класів стандартного та академічного рівнів.

Задача 2.20 Швидкий потяг за розкладом повинен був пройти залізничний перегін АВ без зупинки за 4 год. Але на відстані 150 км від А його затримали на 20 хв. Щоб прибути на станцію В за розкладом, потяг пройшов решту шляху з швидкістю на 15 км/год. більшою, ніж початкова. Знайти довжину перегону АВ.

Розв’язання задачі

Нехай х км – довжина перегону. Тоді швидкість потяга за розкладом км/год, а після зупинки він рухався із швидкістю ( + 15) км/год. Отже, до зупинки він рухався 150 : = (год.), а після зупинки –

 

З урахуванням часу, затраченого на зупинку, потяг пройшов залізничний перегін за ( + + ) (год.), що за умовою дорівнює 4. Складемо рівняння:

+ + = 4,

Розв’яжемо його:

+ - = 0,

3(600х + 36000 + 4х² – 600х) – 11х² – 660х = 0,

х² – 660х + 108000 = 0,

х₁ = 300, х₂ = 360.

Перевірка показує, що обидва корені рівняння задовольняють умову задачі.

Відповідь. 300 км або 360 км.

Задача 2.21  Один завод мав виготовити 720 верстатів, а другий за той самий строк – 660 верстатів. Перший завод, виготовляючи щодня на 10 верстатів більше від другого, виконав замовлення на два дні раніше строку, а другий завод, виготовивши 22 верстати понад план, закінчив роботу на один день раніше строку. Скільки верстатів виготовляв щодня кожний завод?

Розв’язання задачі

Позначимо через х кількість верстатів, що їх щодня виготовляв другий завод. Тоді, за умовою задачі, кількість верстатів, які виготовляв щоденно перший завод, буде (х + 10). За цих умов перший завод виконав замовлення за днів, а другий завод працював днів (660 + 22 = 682). Перший завод виконав замовлення на 2 дні раніше строку, тобто робота була розрахована на ( + 2) дні. Другий завод закінчив роботу на один день раніше строку, тобто робота була розрахована на (+1) днів. Для обох заводів був встановлений однаковий строк виконання замовлення, отже, маємо рівняння:

+ 2 = +1,

-   + 1 = 0,

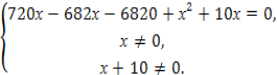
х² + 48х – 6820 = 0,

х₁ = 62, х₂ = -110.

Другий корінь не задовольняє умову задачі. Отже, х = 62, тобто другий завод щодня виготовляв 62 верстати. Перший завод щоденно виготовляв 62 + 10 = 72 (верстати).

Відповідь. 72 верстати, 62 верстати.

4. Апробація основних результатів дослідження

Як слушно зауважив колись відомий критик-демократ Д.І. Писарєв: «Математика не тільки готує учня до природничих наук, вона ще, крім того, готує з нього безстрашного працівника, для якого праця і нудьга стають двома поняттями, що взаємно виключають одне одне».

Для детальнішого дослідження даної теми був проведений експеримент. До дослідження були залучені учні 7 – А та 7 – Б класів однієї з загальноосвітніх шкіл міста. Звіти за попередні роки свідчать про те, що рівень навчальних досягнень цих учнів приблизно однаковий. (табл. 3, діаграма 1)

Таблиця 3

Клас	Учнів в класі	Початковий рівень		Середній рівень		Достатній рівень		Високий рівень
		учнів	Їх у %	учнів	Їх у %	учнів	Їх у %	учнів	Їх у %
7 – А	26	2	7,7	5	19,2	15	57,7	4	15,4
7 – Б	25	3	12	4	16	13	52	5	20

 

Діаграма 1

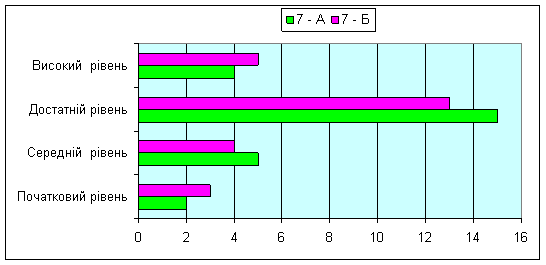
Експеримент полягав у тому, що в одному з цих класів був проведений цикл уроків з елементами прикладної математики (8 годин). Один з таких уроків представлено у додатку 3. Завдяки сучасним комп’ютерним технологіям (наявність в класі мультимедійної дошки) уроки були підкріплені великою кількістю фотографій та графічних зображень, що дозволило проводити роботу більш ефективно.

На кожному уроці було присутнє незалежне журі (вчитель методист  з математики та завуч з навчально-виховної роботи ). Після кожного уроку вони висловлювали свої зауваження та пропозиції, які враховувались в подальшій роботі. Наприкінці досліду вони підвели такий загальний підсумок:

Завуч з навчально-виховної роботи: «Мета експерименту була досягнута, що підтверджують результати контрольної роботи. Вибір методів навчання, організаційних форм і засобів був вдалим, про що свідчить результативність проведених уроків. Використання сучасних інформаційних технологій навчання значною мірою сприяли інтенсифікації навчально-виховного процесу, активізації пізнавальної діяльності та розвитку творчого мислення. Запропонована методика була прийнята до відома всіх вчителів математики нашої школи на позачергових зборах методичного об’єднання вчителів фізико-математичних дисциплін та запротокольована (Протокол № 7 від 22.12.2011)».

Вчитель методист  з математики: «Система уроків вчителя була побудована таким чином, що створилися оптимальні умови для сприйняття матеріалу, його усвідомлення, запам’ятовування головного в ньому, використання засвоєний знань до розв’язування текстових задач, глибшого і міцнішого оволодіння математичними знаннями, навичками й уміннями. Актуалізація опорних знань була проведена на достатньо високому рівні, що дозволило «тримати» учнів в піднесеному настрої та високому темпі роботи протягом всіх уроків, а використання наочностей тільки підбурювало зацікавленість школярів.»

Для оцінки результатів дослідження була проведена в цих класах контрольна робота з однаковими завданнями. Результати виявились неочікуваними. Аналіз основних помилок показав, що у класі де проводився експеримент були допущені помилки під час обчислень, а в іншому класі проблеми виникали при розв’язувані задач, а саме при виборі невідомого та складанні основного рівняння за умовою.

Діаграма 2 результатів виконання

контрольної роботи №2 з алгебри в 7 – А та 7 – Б класах

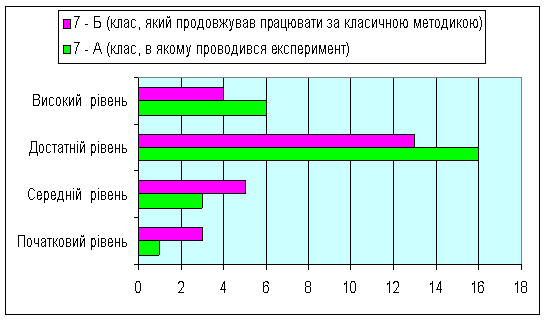
Висновки

У даній магістерській роботі запропоновано методику розв’язування прикладних задач методом рівнянь в основній школі, яка реалізується у три етапи: підготовка, ознайомлення і формування відповідних умінь. Під час підготовчої роботи до введення текстової задачі формуємо у школярів уміння порівнювати задачі, аналізувати умову, шукати способи розв’язання задачі; ознайомлюючи дітей з текстовими задачами, вчимо розв’язувати задачі аналітичним способом і розкладати складені задачі на прості; формуючи уміння і навички розв’язування прикладних задач, ми продовжуємо вчити дітей розв’язувати задачі аналітичним способом та розкладати складені задачі на прості, на підставі чого складати план розв’язування, формувати уміння порівнювати задачі, а також узагальнюємо структуру однотипних задач.

Під час введення даної теми розвиваємо варіативність мислення учнів, його гнучкість та глибину, свідомість розумових процесів школярів за допомогою спеціальних завдань. Звертаємо увагу на постановку запитання до даної умови; складання задач; розв’язування задач з зайвими даними чи недостатньою кількістю числових даних; на порівняння подібних задач; узагальнення структур задач.

У даній магістерській роботі вивчалися історичні аспекти підвищення продуктивності навчання учнів розв’язувати текстові задачі на уроках алгебри в основній школі. Як ми побачили, що навчити учнів розв’язувати прикладні задачі не так то вже і просто. Виходячи з думки вчених, вчителів можна говорити про те, що у методиці навчання учнів розв’язувати прикладні задачі не може бути єдиного і конкретного зразка для пояснення матеріалу. Це зумовлено, насамперед, розумовими здібностями учнів і не до кінця сформованими вміннями та навичками при розв’язуванні простих задач.

Методика може запропонувати лише певні види вправ і запитань, які доцільно проводити перед вивченням текстових задач, а кожен вчитель має можливість встановити свій порядок у їх виборі.

У напрямку удосконалення шляхів навчання учнів розв’язувати прикладні задачі в школі працює багато вчених. Теоретичний матеріал, який нам подано у методиці навчання математики широко розкриває всі питання, і конкретно пояснює той чи інший вид роботи над задачами.

Для ефективного розв’язування текстових задач ще у початкових класах потрібно прививати любов і цікавість до математики і зокрема до задач. Але як свідчить практика, більшість дітей не просто не вміють розв’язувати задачі, а й не люблять. А цю нелюбов можна пояснити декількома факторами: добір учнів у класі, ставлення батьків до навчання своїх дітей, досвід учителя, неправильне перше ознайомлення із задачею, відсутність диференційованого підходу в навчанні дітей розв’язувати задачі, недостатня робота над її змістом, а ще тим, що вчитель на уроці “женеться” за кількістю розв’язаних завдань і не зважає на потреби і бажання дітей. Психологія нам каже, що учень хоче творити, а творити може кожен. Як же бути з уроками математики? Тут простим запевненням “ти це зможеш” не допомогти. Деяким дітям особливо важко дається розв’язання задач. І знову: що робити? Чому школярі не люблять розв’язувати задачі? Тому що не вміють. Як же навчити учнів не тільки розв’язувати прикладні задачі, а ще й викликати інтерес до них? Тут доцільно, при розв’язуванні задач, давати дітям запитання, які б розкривали зміст задачі, ставили додаткові запитання до задачі. Можна запропонувати безліч різних завдань, аби у дітей виникла цікавість до математики. У підручниках з алгебри чітко визначено, чого саме повинні навчити дітей, але в них не можна передбачити необхідну кількість тренувальних вправ для кожного конкретного класу. Тому цю проблему, виходячи з необхідності, має вирішувати сам учитель. Тому доцільно спочатку подати деякі вправи з підручника, для вивчення розв’язування задач певного виду, а потім потрібно використовувати додаткові джерела.

На сьогоднішній день широкого застосування набувають інтегровані уроки, а також інтегровані завдання на уроках. Урок з алгебри теж не є винятком. Доцільно розв’язувати з учнями задачі, які містять тексти, пов’язані з географією, історією.

Нами підібрана добірка завдань для підвищення ефективності методики формування вмінь розв’язувати прикладні задачі. Мета формуючого експерименту полягала у перевірці даної добірки завдань для формування у середніх школярів загального вміння розв’язування текстових задач шляхом порівняльного аналізу результатів виконання контрольної роботи у контрольному і експериментальному класах, цілеспрямованих педагогічних спостережень у класах, де проводилося дослідне навчання. Досвід показує, що учні з великим інтересом розв’язують прикладні задачі, виявляють кмітливість і творчу самостійність. Також одним із важливих засобів організації цілеспрямованої і систематичної роботи щодо розвитку учнів є різні задачі з логічним навантаженням. Виконуючи їх, учні оволодівають новими знаннями, прийомами розумової діяльності, закріплюють та вдосконалюють вміння та навички.

Отже, всі ці та інші види роботи на уроці алгебри, можна вирішити одне з найголовніших завдань, яке стоїть сьогодні перед учителем на цьому етапі навчання – це навчити учнів розв’язувати прикладні задачі.

Список використаних джерел

 

1. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики: Навч. Посібник. – К.: Вища школа, 2001. – 271 с.
2. Ачкан В. Прикладні задачі як засіб формування математичних компетентностей учнів у процесі вивчення рівнянь і нерівностей в курсі алгебри і початків аналізу // Математика в школі. – 2009. – №1-2. – С. 31-34.
3. Бевз Г. П. Методика викладання математики: посібник. – вид. 2-ге, переробл. і доповн. / Г. П. Бевз. – К. : Вища шк., 1977. – 376 с.
4. Бевз Г. П. Алгебра: підруч. для 7 кл. загальноовіт. навч. закл. / Г. П. Бевз, В. Г. Бевз. – К. : Зодіак-ЕКО, 2007. – 224 с.
5. Дубинчук О. С. Методика викладання алгебри 7 – 9 класах: посібник для вчителя. / О. С. Дубинчук, Ю. І. Мальований, Н. П. Дичек. – К. : Рад. шк.., 1991. – 254 с
6. Жалдак М.І. Комп’ютер на уроках математики: Посібник для вчителів. – К.: Техніка, 1997. – 303 с.
7. Забранський В., Вінніченко Н. Прикладні задачі економічного змісту і функції // Математика в школі. – 2011. - №1-2. – С.22-26.
8. Забранський В., Грицик Т. Прикладні задачі під час вивчення лінійних та квадратних рівнянь // Математика в школі. – 2010. - №12. – С.52-60.
9. Книга для вчителя математики: Довідково-методичне видання / Упоряд Н.С. Прокопенко, Н.П. Щекань. – Харків: ТОРСІНГ ПЛЮС, 2005. – 272 с.
10. Концепція математичної освіти 12-річної школи: Проект // Математика в школі. – 2002. - №2. – С. 12-17.
11. Концепція профільного навчання в старшій школі // Інформ. зб. МОН України. – 2003. № 24. –С. 32.
12. Колініченко О., Колініченко Н. Застосування математичних знань у викладанні хімії ті біології // Рідна школа. – 2003. - № 24. – С.32.
13. Кравчук В. Алгебра: підруч. для 7 кл. загальноовіт. навч. закл / В. Кравчук, М. Підручна, Г. Янченко. – Тернопіль, 2005. – 223 с.
14. Костевська Л. Задачі на спільну роботу. Алгебра, 8 клас / Л. Костевська // Математика. – К. : пед. преса, 2005, №10 (310). – С. 14 - 15.
15. Лаврик В.І. Методи математичного моделювання в екології. – Київ: Фітосоціоцентр, 1998. – 132 с.
16. Програми для загальноосвітніх навчальних закладів. Математика.

5-11 класи (авт. В.Г. Бевз, А.Г. Мерзляк, З.І. Слєпкань) Міністерство освіти і науки України. – К.: Навчальна книга, 2003. - С. 4-52.

17. Програма для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв природничого профілю. Математика. 10-11 класи (авт. Я.Б. Бродський, О.Л. Сліпенько, О.М. Афанасьєва). Міністерство освіти і науки України. – К.: Навчальна книга, 2003. – С. 70-132.
18. Програми для загальноосвітніх навчальних закладів. Математика. 5-12  класи. Міністерство освіти і науки України. – К.: Ірпінь, 2005. – 64 с.
19. Слєпкань З. І. Методика навчання математики: підручник. – 2-ге вид., доповн. і переробл. / З. І. Слєпкань. – К. : Вища шк., 2006. – 582 с.
20. Соколенко Л.О., Філон Л.Г., Швець В.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу: практикум. Навчальний посібник. – Київ: НПУ імені М.П. Драгоманова, 2010. – 128 с.
21. Філімонова М.О., Швець В.О. Математичне моделювання в курсі математики основної школи: зміст і вимоги до підготовки учнів // Дидактики математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – вип..34 – Донецьк: Вид-во ДонНу, 2010.
22. Фридман Л. М. Как научиться решать задачи. Пособие для учащихся. 2-е изд., перераб. і доп. / Л. М. Фридман, Е. Н. Турецкий. – М. : Просвещение, 1984. – 175 с.
23. Швець В.О., Білянін Г.І. Математика: Навчальний посібник. – Чернівці: Зелена Буковина, 2003. – 382 с.
24. Швець В.О., Прус А.В. Теорія та практика прикладної спрямованості шкільного курсу стереометрії: Навчальний посібник. – Житомир: Видавництво ЖДУ імені І.Франка, 2007. – 156 с.