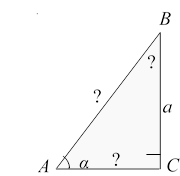
Розв’язування прямокутних трикутників
Нестандартний урок на тему: "Розв'язування прямокутних трикутників.
Мета:
навчальна – закріпити та систематизувати знання учнів про вивчені спів¬відношення між сторонами і кутами в прямокутному трикутнику та їх властивості. Відпрацювати навички застосовувати набуті знання для розв'язування прямокутних трикутників та задач на знаходження еле¬ментів інших фігур.
розвиваюча – розвивати пізнавальні інтереси, уміння визначати головні цілі навчання, уміння вести конспект, пам'ять;
виховна – виховувати культуру учнів, увагу, акуратність, дисциплінованість.

ПЛАН-КОНСПЕКТ УРОКУ
Вчитель: Коваль Артем Васильович
Клас: 8
Предмет: геометрія
Тема. Розв’язування прямокутних трикутників
Урок № 59 Тема уроку. Розв’язування прямокутних трикутників.
Мета:
v навчальна– закріпити та систематизувати знання учнів про вивчені співвідношення між сторонами і кутами в прямокутному трикутнику та їх властивості. Відпрацювати навички застосовувати набуті знання для розв'язування прямокутних трикутників та задач на знаходження елементів інших фігур.
v розвиваюча – розвивати пізнавальні інтереси, уміння визначати головні цілі навчання, уміння вести конспект, пам'ять;
v виховна – виховувати культуру учнів, увагу, акуратність, дисциплінованість.
Обладнання: дошка, крейда, підручник «Геометрія 8 клас», план-конспект уроку, картки з завданнями.
Тип уроку: застосування знань, умінь і навичок;
Хід уроку:
Етап 1. Організація класу.
Заходжу в клас вітаюся з учнями. Пропоную учням сісти групами по 5 чоловік і підготувати все необхідне для уроку. Відмічаю відсутніх.
Епіграф уроку:
Світ, що нас оточує , – це світ геометрії.
Тож давайте його пізнавати!
Піфагор
Етап 2. Перевірка домашнього завдання
Перевірку здійснюють у кожній групі консультанти і їхні помічники. Учитель перед уроком перевіряє виконання домашнього завдання у консультантів і надає їм необхідні інструкції.
Етап 3. Актуалізація опорних знань
Фронтальне опитування(метод незакінчених речень):
1. Відношення протилежного катета до прилеглого це …
2. Відношення прилеглого катета до гіпотенузи це …
3. Сторона, що лежить на проти кута 90° це …
4. Одна з сторін що утворює прямий кут це …
5. Відношення протилежного катета до гіпотенузи це …
6. Найбільша сторона прямокутного трикутника …
Вправа знайди помилку
|
|
|
Етап 4. Розв’язування вправ
Цікаво знати
Піфагор брав участь у кулачному бою на 58 Олімпіаді, яка проходила у 548 році до н.е. Переказують, що судді не хотіли допустити його до змагань через малий зріст. На що Піфагор відповів: «Можливо мій вигляд не викликає у вас довіри, але я буду наносити удари з такою математичною точністю, що супернику буде жарко». І він дотримав свого слова – став чемпіоном з цього виду спорту й утримував цей титул ще на кількох олімпіадах.
Колективне розв’язування прикладних задач:
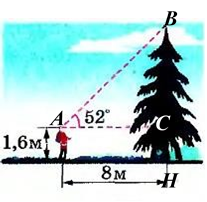 615. (За Мерзляком) . За рисунком знайдіть висоту ялинки.
615. (За Мерзляком) . За рисунком знайдіть висоту ялинки.
Розв’язання
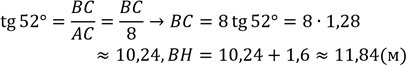
В.: 11,84 м.
Цікаво знати
На прикінці ХІХ ст. було відкрито на Марсі «канали», що тривалий час вважалися штучними для налагодження зв’язку з марсіанами на виличезному просторі Західносибірської низовини запропонували побудувати гіганську геометричну фігуру, що світилася б, - рисунок теореми Піфагора, бо вважали що ця теорема справедлива скрізь і що жителі будь-якої планети повинні зрозуміти такий сигнал. Передбачили, що марсіани, побачивше це зображення, зроблять висновок, що на Землі живуть розумні істоти, і дадуть відповідь також мовою математики. Адже математику вважають універсальною мовою
Всесвіту.
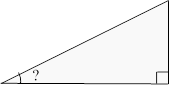
1026. (За Бурдою). За 800 метрів від місця підйому літака ростуть дерева висотою до 20 м. Під яким кутом має підніматися літак, щоб не зачіпити дерево.
Розв’язання
B
![]()
20 м
В.: 𝛼 > 1,26′.
AC
800 м
Цікаво знати
Один професор скористався теоремою Піфагора на практиці. Йому запропонували ліжко, що виявилося коротким для нього. Професор виміряв довжину ліжка а, його ширину b і обчислив з точністю до міліметра, що його довжина менша від ![]() . Тоді він ліг на ліжко по діагоналі, остаточно впевнений у великій практичній користі теореми Піфагора.
. Тоді він ліг на ліжко по діагоналі, остаточно впевнений у великій практичній користі теореми Піфагора.
Робота в групах з задачами за готовими рисунками (метод мозковий штурм)
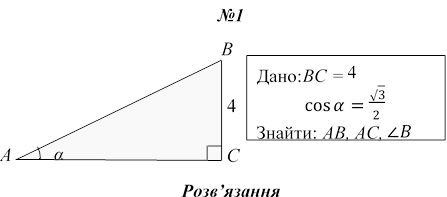
1.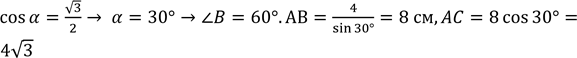
Захист робіт
Учні пояснюють розв’язування задач, супроводжуючи пояснення записами на дошці. Після захисту задач групи ставлять одна одній питання.
Цікаво знати
 «Ослячий міст» - так називали теорему Піфагора у Франції та Німеччині в епоху середньовіччя. Учні, які заучували теорему на пам'ять не розуміючи її були прозвані «віслюками». Вона для них була містком який вони не змогли перейти.
«Ослячий міст» - так називали теорему Піфагора у Франції та Німеччині в епоху середньовіччя. Учні, які заучували теорему на пам'ять не розуміючи її були прозвані «віслюками». Вона для них була містком який вони не змогли перейти.
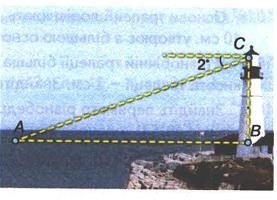 1029. (За Бурдою). З башти висотою 75 м над рівнем моря видно корабель під кутом 2°. Знайдіть відстань від корабля до маяка.
1029. (За Бурдою). З башти висотою 75 м над рівнем моря видно корабель під кутом 2°. Знайдіть відстань від корабля до маяка.
Розв’язання

В.: 2147,7 м.
Цікаво знати
 У 1955 р. у Греції було випущено поштова марка, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитись у тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
У 1955 р. у Греції було випущено поштова марка, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитись у тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Етап 5. Підведення підсумків уроку
Даю відповіді на питання, які виникли підчас уроку. Коментоване оцінювання учнів.
Рефлексія:
vЧи задоволені ви своєю роботою?
vЗ яким настроєм ви працювали на уроці?
vЩо вам запам’яталось на уроці?
vЧи було вам комфортно на уроці?
vДе вам стануть в пригоді здобуті знання?
Релаксація:
(Розглядання геометрична оптичної ілюзії(рух кіл))
Етап 6. Постановка домашнього завдання
Повторити: §18с. 131-132 (за Мерзляком) § 31с. 174-177 (за Апостоловою)
Розв’язати: 612, 616 с. 134-135 (за Мерзляком)


про публікацію авторської розробки
Додати розробку