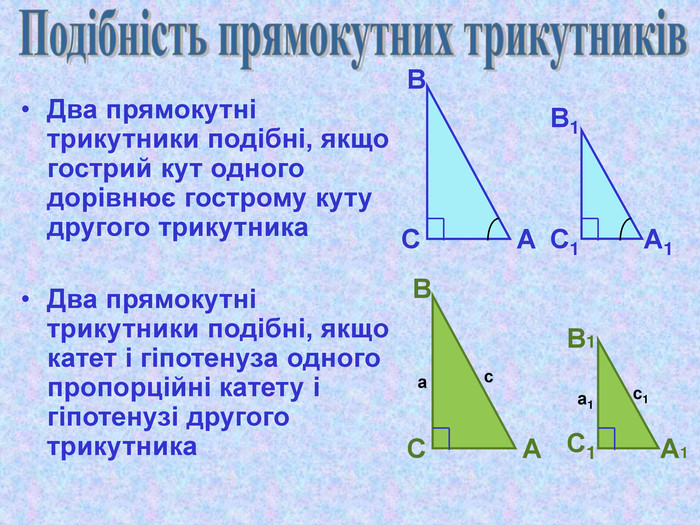
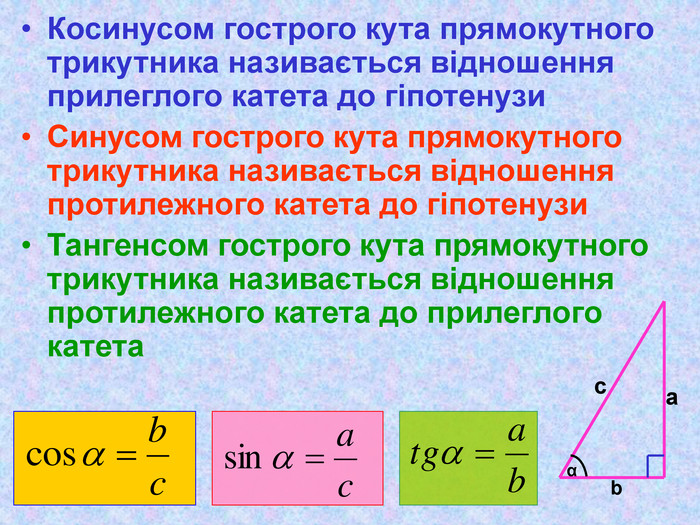
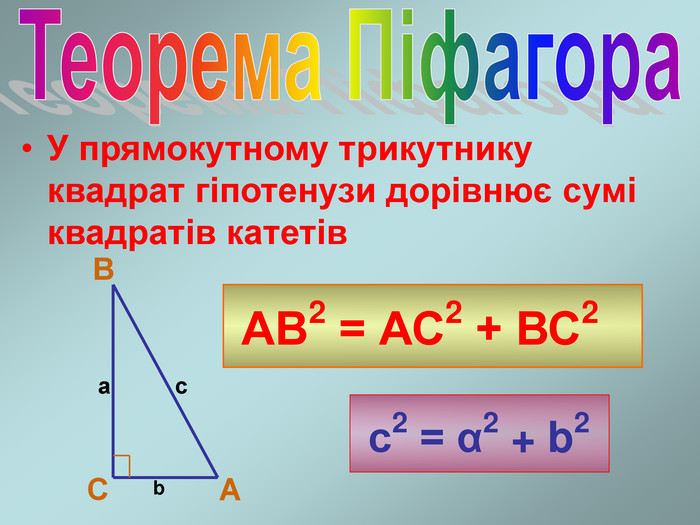
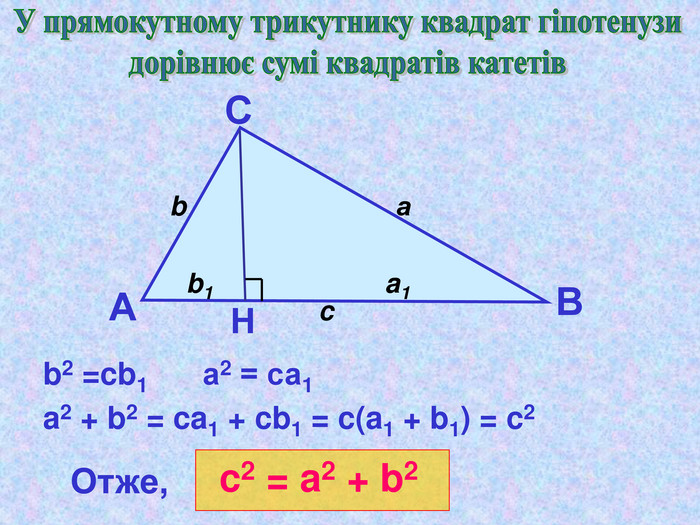
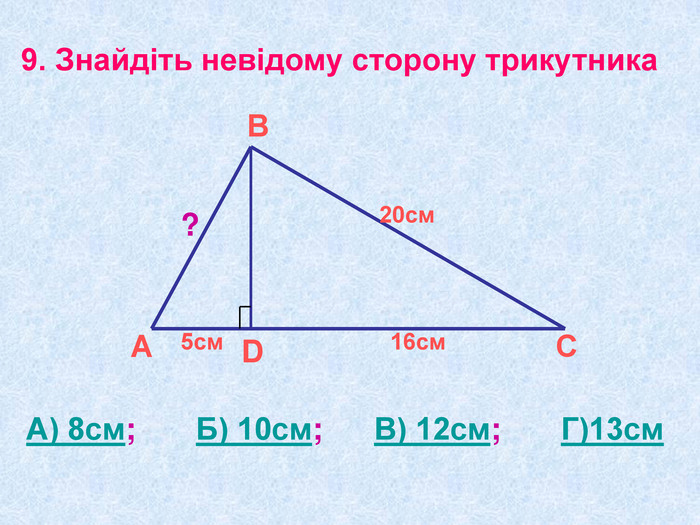
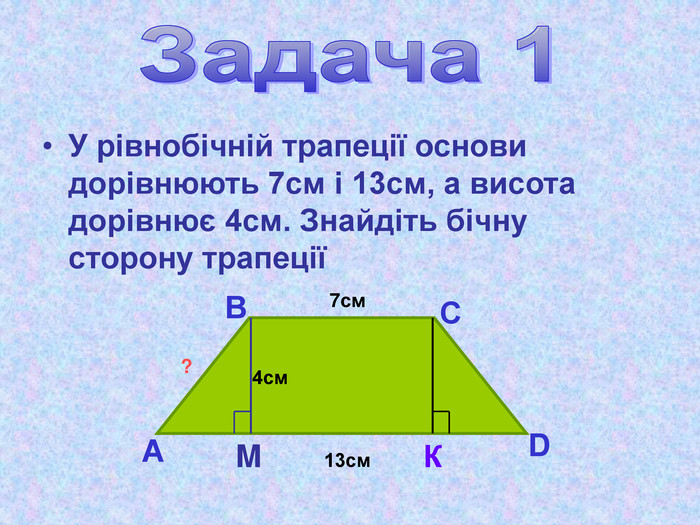
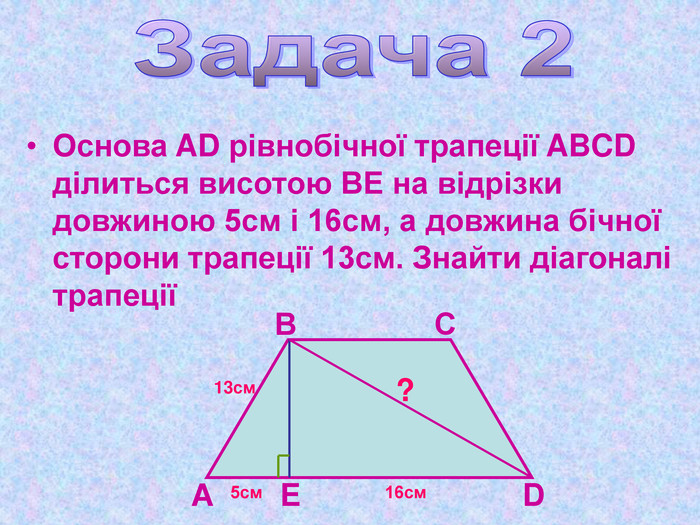
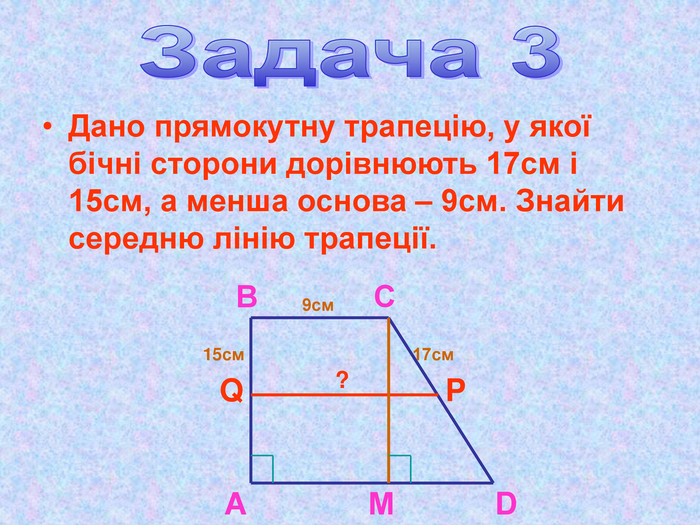
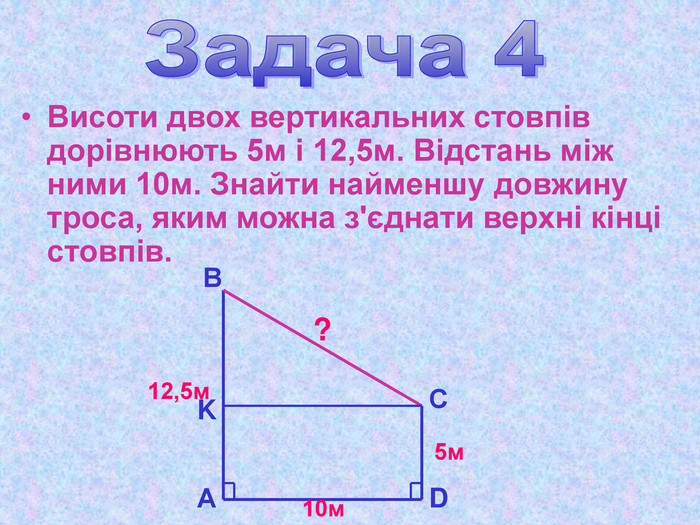
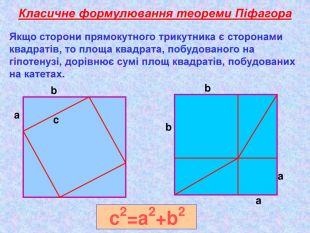
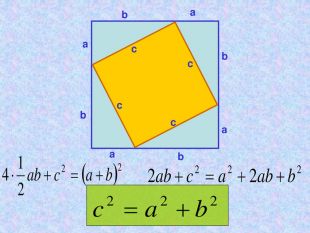
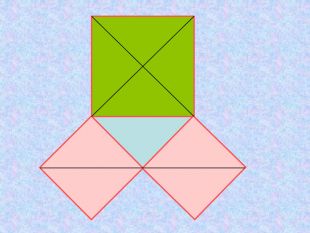
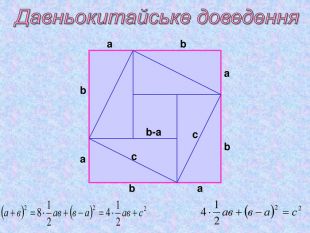
Презентація "Теорема Піфагора"
Про матеріал
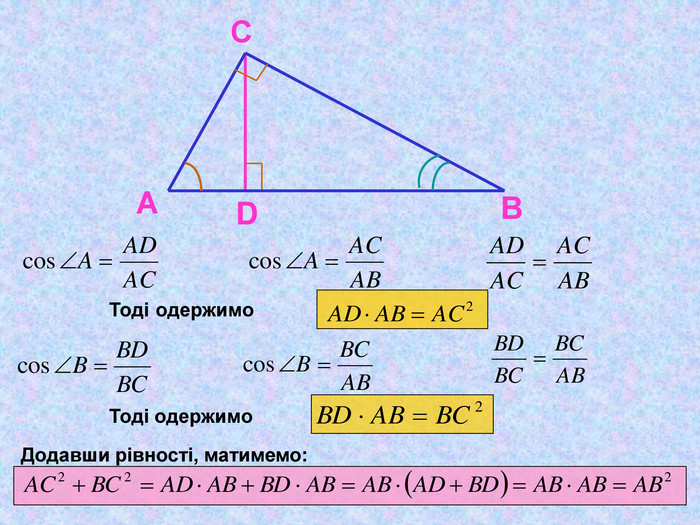
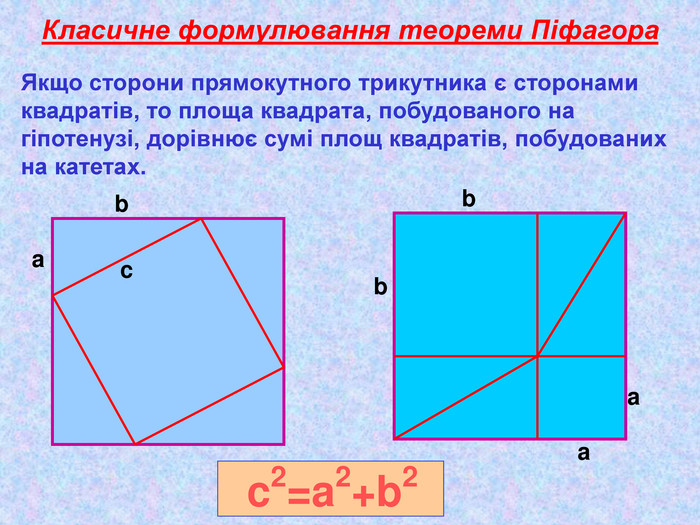
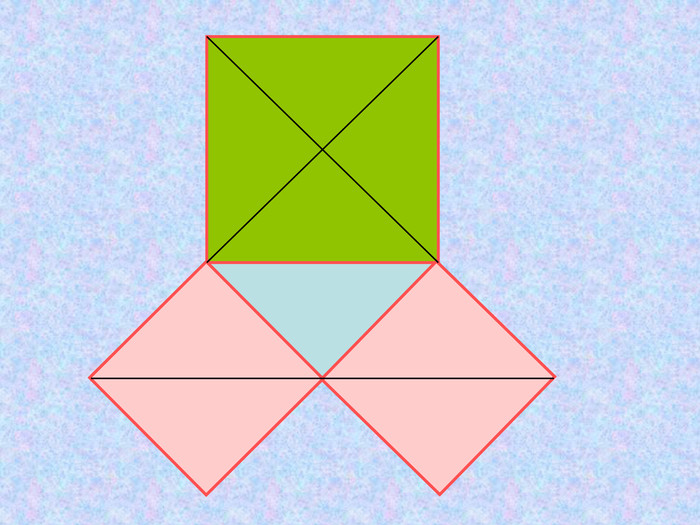
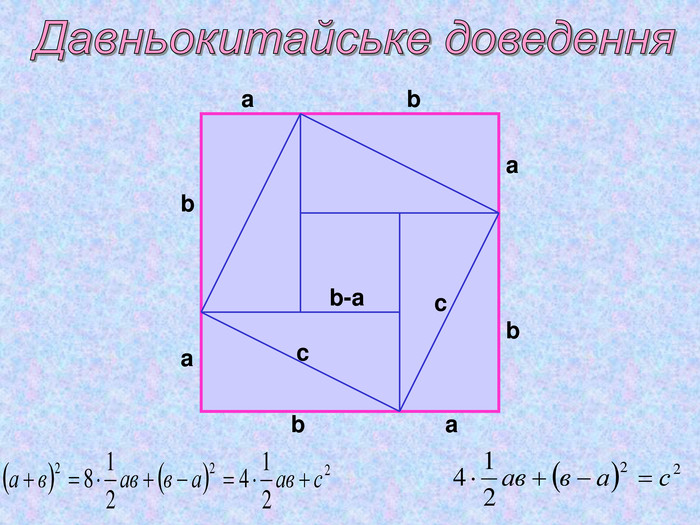
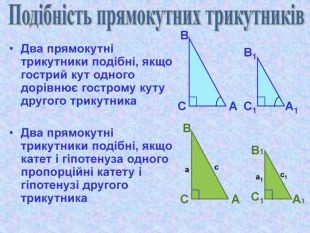
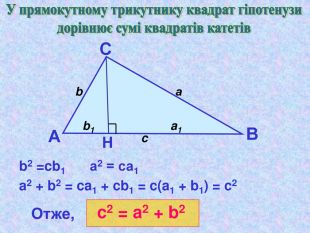
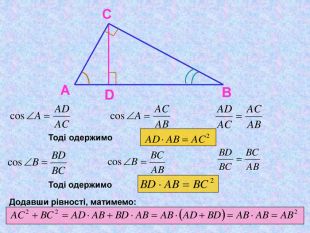
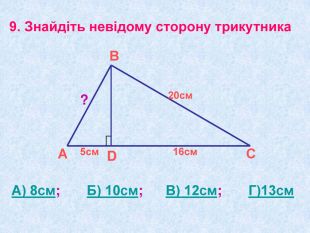
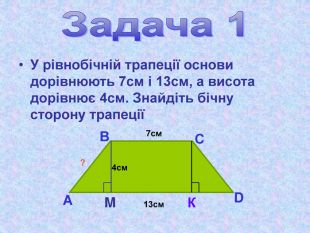
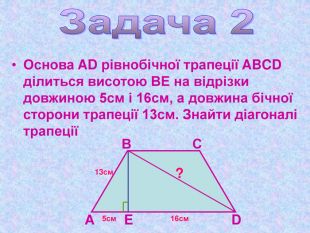
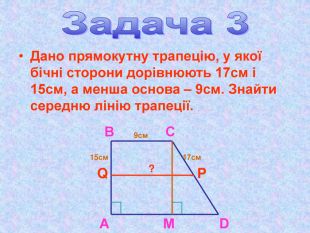
Матеріал презентації "Теорема Піфагора" сприяє узагальненню та систематизації знань учнів, ознайомленню дітей з різними способами доведення теореми Піфагора, допомагає вдосконалювати вміння та навички учнів застосовувати теорему Піфагора при розв'язуванні задач та виконанні тестових завдань Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку