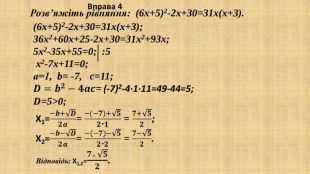Розв’язування рівнянь, що зводяться до квадратних

Розв’язування рівнянь, що зводяться до квадратних

𝒙𝟐−𝒚𝟐=(𝒙−𝒚)(𝒙+𝒚)  Розв’яжіть рівняння 2𝑥3−8𝑥=0. Розв’язання:2𝑥3−8𝑥=0;Застосуємо винесення спільного множника за дужки та використаємо формули скороченого множення:2𝑥𝑥2−4=0;                                            2𝑥𝑥−2𝑥+2=0; 2x=0, або x-2=0, або x+2=0; х1 =0; х2=2; х3=−2. Відповідь: х1 =0; х2=2; х3=−2. І метод Розкладання на множники. Добуток дорівнює нулю тоді, коли хоча б один з множників дорівнює нулю.abc=0 або a=0, або b=0, або c=0 Запам’ятайте!!!Рівняння n-го степеня має не більше ніж n коренів. Вправа 1

Запам’ятайте!!!Рівняння n-го степеня має не більше ніж n коренів. Розв’яжіть рівняння 5𝑥3−2𝑥2+10𝑥−4=0. Розв’язання: Застосуємо розкладання на множники способом групування:5𝑥3−2𝑥2+10х−4=0; 5𝑥3+10𝑥−(2𝑥2+4)=0;5𝑥𝑥2+2−2𝑥2+2=0; 𝑥2+25𝑥−2=0;𝑥2+2=0  або  5𝑥−2=0;𝑥2=−2;                5𝑥=2; Розв’язків немає; 𝑥=25=0,4. Відповідь: 𝑥=0,4. Вправа 2 І метод Розкладання на множники

Розв’язання  (х – 1)2 + 11 – 2х(х – 3) = 0;х2 – 2x + 1 + 11 – 2х2 + 6x = 0 ;-х2 + 4х + 12 = 0;х2 – 4х – 12 = 0;за теоремою Вієта𝑥1+𝑥2=4,𝑥1𝑥2=−12;  𝑥1=−2,𝑥2=6.х1 = -2 , х2 = 6    Відповідь: х1 = -2 , х2 = 6. Розв’яжіть рівняння (х – 1)2 + 11 = 2х(х – 3). Вправа 3 ІІ метод Розкриття дужок

Розв’язання   2𝑥𝑥−5+5=𝑥;2𝑥𝑥−5+5−𝑥=0; 2𝑥2−10𝑥+5−𝑥=0; 2𝑥2−11𝑥+5=0;𝑎=2;𝑏=−11; 𝑐=5;𝐷=𝑏2−4𝑎𝑐=−112−4·2·5=121−40=81 𝐷=81=9 𝑥1=11+94=204=5 𝑥2=11−94=24=12=0,5 Відповідь: 𝑥1=5, 𝑥2=0,5 Розв’яжіть рівняння 2𝑥𝑥−5+5=𝑥. Вправа 3 ІІ метод Розкриття дужок

Розв’яжіть рівняння: (6x+5)2-2x+30=31x(x+3). Вправа 4(6x+5)2-2x+30=31x(x+3);36x2+60x+25-2x+30=31x2+93x;5x2-35x+55=0; :5 x2-7x+11=0;а=1, b= -7, c=11;𝑫=𝒃𝟐−𝟒𝒂𝒄= (-7)2-4·1·11=49-44=5;𝑫=5>0; Х1=−𝒃+𝑫𝟐𝒂= −(−𝟕)+𝟓𝟐·𝟏 = 𝟕+𝟓𝟐; Х2=−𝒃−𝑫𝟐𝒂= −−𝟕−𝟓𝟐·𝟐 = 𝟕−𝟓𝟐. Відповідь: Х1,2=𝟕± 𝟓𝟐. 

ІІІ метод Зведення рівняння до квадратного способом заміни змінних. Рівняння виду 𝑎𝑥4+𝑏𝑥2+𝑐=0, де x-змінна, a, b,c – числа, причому 𝑎≠0, називають біквадратним Метод заміни змінноїВводимо нову змінну t таку, що 𝑥2=𝑡   𝑡>0,   𝑥4=(𝑥2)2= 𝑡2 Тоді біквадратне рівняння 𝑎𝑥4+𝑏𝑥2+𝑐=0, відносно змінної x перетворюється у квадратне рівняння відносно змінної t: 𝑎𝑡2+𝑏𝑡+𝑐=0. 

Розв’яжіть рівняння: x4-3x2-4=0. Вправа 5x4-3x2-4=0 ;Позначимо x2=t, t>0; x4= t2t2-3t-4=0;а=1, b= -3, c=-4;за теоремою Вієтаt1+t2=3,t1t2=−4;  t1=−1,t2=4. Повертаємось до заміни: x2=tx2= -1; або x2=4;Коренів немає х1 = -2 , х2 =2.    Відповідь: х1 =-2 , х2 =2. ІІІ метод Зведення рівняння до квадратного способом заміни змінних

Знадіть корені рівняння 2х4−7х2−4=0 Розв’язання: Використаємо метод заміни змінної.х2=𝑦, тоді х4=(х2)2=𝑦2. Запишемо задане рівняння з використанням змінної y: 2𝑦2−7𝑦−4=0. Розв’яжемо отримане квадратне рівняння 2𝑦2−7𝑦−4=0;  𝑎=2, 𝑏=−7, 𝑐=−4;𝐷=𝑏2−4𝑎𝑐;    𝐷=−72−4∙2∙−4=49+32=81,      𝐷>0.𝑦1=7+92∙2=164=4;           𝑦2=7−92∙2=−24=−12. Повернемося до початкової змінної х2=𝑦:𝑦1=4       або          𝑦2=−12;𝑥2=4  або 𝑥2=−12. Розв’яжемо отримані неповні квадратні рівняння:𝑥2=4  або 𝑥2=−12. 𝑥=±2;          розв′язків немає. Відповідь: ±2 ІІІ метод Зведення рівняння до квадратного способом заміни змінних. Вправа 6

Розв’яжіть рівняння: 2(x-2)2-3(x-2)+6=0. Вправа 72(x-2)2-3(x-2)+1=0;Позначимо x-2=t2t2-3t+1=0а=2, b= -3, c=1;𝑫=𝒃𝟐−𝟒𝒂𝒄= (-3)2-4·2·1=9-8=1;𝑫=1>0; t1=−𝒃+𝑫𝟐𝒂= −(−𝟑)+𝟏𝟐·𝟐 =𝟑+𝟏𝟒= 𝟒𝟒=1; t2=−𝒃−𝑫𝟐𝒂= −−𝟑−𝟏𝟐·𝟐 =𝟑−𝟏𝟒=𝟐𝟒=𝟏 𝟐=0,5;Повертаємось до заміни x-2=t; x-2=1; або x-2=0,5; x=1+2; x=0,5+2;x1=3; x2=2,5. Відповідь: Х1=3, Х2= 2,5. ІІІ Зведення рівняння до квадратного способом заміни змінних

Розв’яжіть рівняння: (x 2 +5х)2-2(x 2 +5х)=24. Вправа 9(x 2 +5х)2-2(x 2 +5х)=24;Позначимо x 2 +5х =t, тоді (x 2 +5х)2 =t 2 t2-2t-24=0а=1, b= -2, c=-24;𝑫=𝒃𝟐−𝟒𝒂𝒄= (-2)2-4·1·(-24)=4+96=100;𝑫=100>0; t1=−𝒃+𝑫𝟐𝒂= −(−𝟐)+𝟏𝟎𝟎𝟐·𝟏 =𝟐+𝟏𝟎𝟐= 𝟏𝟐𝟐=6; t2=−𝒃−𝑫𝟐𝒂= −−𝟐−𝟏𝟎𝟎𝟐·𝟏 =𝟐−𝟏𝟎𝟐=−𝟖𝟐=-4;Повертаємось до заміни x 2 +5х =t ; x 2 +5х =6; або x 2 +5х =-4; x 2 +5х -6=0; x 2 +5х +4=0;за теоремою Вієта за теоремою Вієта𝑥1+𝑥2=−5,𝑥1𝑥2=−6; 𝑥1=−6,𝑥2=1. 𝑥1+𝑥2=−5,𝑥1𝑥2=4; 𝑥1=−4,𝑥2=−1.х1 =-6 , х2 =1;     х3= -4 , х4 = -1    Відповідь: х1 =-6 ; х2 =1; х3= -4 , х4 = -1. ІІІ Метод заміни змінної

Розв’яжіть рівняння: (х2  - 2)2 - 8(х2 - 2) + 7 = 0 Вправа 10(х2  - 2)2 - 8(х2 - 2) + 7 = 0 Позначимо x 2 -2=t, тоді (x 2 -2)2 =t 2 t2-8t+7=0;а=1, b= -8, c=7;за теоремою Вієтаt1+t2=8,t1t2=7;  t1=7,t2=1. Повертаємось до заміни x 2 -2=t ; x 2 -2=7; або x 2 -2=1; x 2=9; x 2 =3;Х1,2= ± 𝟗 Х3,4= ± 𝟑;Х1,2= ± 3;      Відповідь: Х1,2= ± 3; Х3,4= ± 3. ІІІ Метод заміни змінної

Запам’ятайте!!! Необхідною складовою розв’язання раціонального рівняння є обов’язкова перевірка належності знайдених коренів області допустимих значень вихідного рівняння. Значна кількість текстових задач розв’язується за допомогою рівнянь, зокрема дробово-раціональних. Більшість дробово-раціональних рівнянь зводяться до одного з таких: А(х)В(х)=𝟎,  або      А(х)С(х)=В(х)С(х),   або    А(х)С(х)=В(х)𝐃(х) Дані рівняння, у свою чергу, розв’язуються за допомогою рівносильних систем. А(х)В(х)=𝟎;Ах=𝟎,В(х)≠𝟎 А(х)С(х)=В(х)С(х);Ах−Вх=𝟎,С(х)≠𝟎 або Ах=В(х),С(х)≠𝟎 А(х)С(х)=В(х)𝑫(х);Ах𝑫𝒙=Вх𝑪(𝒙),Сх≠𝟎,𝑫𝒙≠𝟎 ІY метод Дробово-раціональні рівняння

Алгоритм розв’язування дробово-раціонального рівняння. Знайдіть область допустимих значень рівняння 𝑄(х)≠𝟎 (обов’язково!!!)Зведіть рівняння до вигляду Р(х)𝑄(х)=0. Використайте правило рівності добутку дробу нулю й розв’яжіть рівняння Р(х)=0. Перевірте, чи задовольняють знайдені роз’язки рівняння P(x)=0 область допустимих значень. (обов’язково!!!) Вилучіть сторонні корені. Запишіть відповідь 

𝑥2𝑥−3=5𝑥𝑥−3;ОДЗ: x ≠3𝑥2𝑥−3−5𝑥𝑥−3=0 𝑥2−5𝑥𝑥−3=0 𝑥2−5𝑥=0𝑥𝑥−5=0 𝑥1=0, 𝑥2=5 Відповідь: 𝑥1=0, 𝑥2=5.  Дробово-раціональні рівняння𝑥2𝑥−3=5𝑥𝑥−3;ОДЗ: x ≠3𝑥2𝑥−3=5𝑥𝑥−3 ·(х-3) 𝑥2=5𝑥;𝑥2−5𝑥=0;𝑥𝑥−5=0; 𝑥1=0; 𝑥2=5;Відповідь: 𝑥1=0, 𝑥2=5. Розв’яжіть рівняння 𝑥2𝑥−3=5𝑥𝑥−3 Оформлення може бути і таким. Вправа 11

Розв’яжіть рівняння 𝑡2−5𝑡+416−𝑡2=0. Розв’язання:𝑡2−5𝑡+416−𝑡2=0;ОДЗ: 16−𝑡2≠0; 𝑡2≠16;           𝑡≠±4;Скористаємося правилом рівності дробу нулю:𝑡2−5𝑡+4=0, 16−𝑡2≠0 Розв’яжемо рівняння 𝑡2−5𝑡+4=0: За теоремою Вієта 𝑡1+𝑡2=5,𝑡1𝑡2=4;  𝑡1=1.𝑡2=4. Перевіримо, чи задовольняють отримані корені ОДЗ рівняння:𝑡1=1 задовольняє ОДЗ;𝑡2=4 не задовольняє ОДЗ. Відповідь: 𝑡=1. ІІ спосіб розв’язання 𝑡2−5𝑡+416−𝑡2=0 Розкладемо тричлен 𝑡2−5𝑡+4 на лінійні множники: 𝑡2−5𝑡+4=(𝑡−1)(𝑡−4)(𝑡−1)(𝑡−4)4−𝑡4+𝑡=0; ;    −𝑡−14+𝑡=0;𝑡−14+𝑡=0;Cкористаємося правилом рівності дробу нулю: 𝑡−1=0,4+𝑡≠0,          𝑡=1,𝑡≠−4;Відповідь: 𝑡=1. Вправа 12

Розв’яжіть рівняння  х+2𝑥=5х+1х+1. х+2𝑥=5х+1х+1;ОДЗ: 𝑥≠0; 𝑥≠−1;Спільним знаменником даних дробів є  х(𝑥+1). х+2𝑥=5х+1х+1; · х(х+1) (х+2)х(х+1)𝑥=(5х+1)х(х+1)х+1; 𝑥+2х+1=5𝑥+1х; 𝑥2+х+2х+2=5𝑥2+х; -4𝑥2+2𝑥+2=0; :(-2)2𝑥2−𝑥−1=0за теоремою Вієта 𝑥1+𝑥2=−0,5,𝑥1𝑥2=−1; 𝑥1=−0,5,𝑥2=1.𝑥1=-0,5 Є ОДЗ, 𝑥2=1 – Є ОДЗ. Відоповідь:𝑥1=-0,5; 𝑥2=1 . Вправа 13

Розв’яжіть рівняння  2𝑥−3+5𝑥+3=14. 2𝑥−3+5𝑥+3=14;ОДЗ: 𝑥≠±3;Спільним знаменником даних дробів є 4(𝑥+3)(𝑥−3). Знаходимо додаткові множники до кожного дробу.2\4(𝑥+3)𝑥−3+5\4(𝑥−3)𝑥+3−1\𝑥2−94=0;8𝑥+3+20𝑥−3−(𝑥2−9)4(𝑥−3)(𝑥+3)=0;Cкористаємося правилом рівності дробу нулю: 8𝑥+24+20𝑥−60−𝑥2+9=0; 𝑥≠±3;−𝑥2+28𝑥−27=0;−𝑥2+28𝑥−27=0      ǀ   ∙−1;𝑥2−28𝑥+27=0;𝑎=1, 𝑏=−28, 𝑐=27;За теоремою Вієта : 𝑥1+𝑥2=28,𝑥1𝑥2=27;       𝑥1=1−задовольняє ОДЗ;𝑥2=27−задовольняє ОДЗ. Відповідь: 1 ; 27.  Вправа 14

Розв’яжіть рівняння 7𝑥−1−12𝑥+1=𝑥2+13𝑥2−1. ОДЗ: x ≠ ± 1 Спільним знаменником є (𝑥−1)(𝑥+1).7𝑥−1−12𝑥+1−𝑥2+13𝑥2−1=0; 7𝑥+1−12𝑥−1−(𝑥2+13)(𝑥−1)(𝑥+1)=0; 7𝑥+1−12𝑥−1−𝑥2+13=0; 7𝑥+7−12𝑥+12−𝑥2−13=0;𝑥2+5𝑥−6=0 ;за теоремою Вієта 𝑥1+𝑥2=−5,𝑥1𝑥2=−6; 𝑥1=−6,𝑥2=1.𝑥1=-6 Є ОДЗ, 𝑥2=1 –не належить ОДЗ. Відоповідь: х=-6. Вправа 15

Розв’яжіть рівняння 7𝑥−1−12𝑥+1=𝑥2+13𝑥2−1 ОДЗ: x ≠ ± 1 Спільним знаменником є (𝑥−1)(𝑥+1). Домножимо всі доданки лівої і правої частини рівняння на спільний знаменник (𝑥−1)(𝑥+1)7𝑥−1−12𝑥+1−𝑥2+13𝑥2−1=0; ·(х-1)(х+1) 7·(х−1)(х+1)𝑥−1−12·(х−1)(х+1)𝑥+1−(𝑥2+13)·(х−1)(х+1)𝑥2−1=0;7𝑥+1−12𝑥−1−𝑥2+13=0; 7𝑥+7−12𝑥+12−𝑥2−13=0; 𝑥2+5𝑥−6=0; за теоремою Вієта 𝑥1+𝑥2=−5,𝑥1𝑥2=−6; 𝑥1=−6,𝑥2=1.𝑥1=-6 Є ОДЗ, 𝑥2=1 –не належить ОДЗ. Відоповідь: х=-6. Вправа 15 ( ІІ спосіб оформлення розв’язання)

Розв’яжіть рівняння 4𝑥2−10𝑥+25−1𝑥+5=10𝑥2−25 ОДЗ: x ≠ ± 5 Спільним знаменником є (𝑥−5)2(𝑥+5). Домножимо всі доданки лівої і правої частини рівняння на спільний знаменник (𝑥−5)2(𝑥+5)4𝑥2−10𝑥+25−1𝑥+5=10𝑥2−25; ·(𝑥−5)2(𝑥+5) 4(𝑥−5)2(𝑥+5)  𝑥2−10𝑥+25−1(𝑥−5)2(𝑥+5)  𝑥+5=10(𝑥−5)2(𝑥+5)  𝑥2−254𝑥+5−1𝑥−52=10𝑥−5; 4𝑥+5−(𝑥2−10𝑥+25)=10𝑥−5; 4𝑥+20−𝑥2+10𝑥−25−10𝑥+50=0; −𝑥2+4𝑥+45=0; 𝑥2−4𝑥−45=0;за теоремою Вієта 𝑥1+𝑥2=4,𝑥1𝑥2=−45; 𝑥1=−5− не належить ОДЗ,𝑥2=9                     Є ОДЗ.       Відоповідь: х=9. Вправа 16 𝑥2−10𝑥+25=(𝑥−5)2𝑥2−25=𝑥−5𝑥+5 

Розв’яжіть рівняння х+3х−4−3𝑥+3=21𝑥2−х−12 𝑥2−х−12=(х+3)(х-4)ОДЗ: x ≠-3; x ≠4; Спільним знаменником є (х+3)(х-4). Домножимо всі доданки лівої і правої частини рівняння на спільний знаменник (х+3)(х-4). х+3х−4−3𝑥+3=21𝑥2−х−12; · (х+3)(х-4). (х+3)(х+3)(х-4)х−4−3(х+3)(х-4)𝑥+3=21(х+3)(х-4)(х+3)(х-4);𝑥+3)(х+3−3(х−4)=21; 𝑥2+6х+9−3𝑥+12−21=0; 𝑥2+3𝑥=0;х(х+3)=0;х=0 або х+3=0;𝑥1=0 Є ОДЗ, 𝑥2=-3 –не належить ОДЗВідоповідь: х=0. Вправа 16 Розкладемо 𝑥2−х−12 на множники 𝑥2−х−12=0;за теоремою Вієта 𝑥1+𝑥2=1,𝑥1𝑥2=−12; 𝑥1=−3,𝑥2=4. 𝑥2−х−12=(х+3)(х-4)