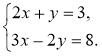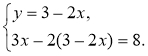Розв'язування систем лінійних рівнянь із двома змінними способом підстановки
Тема. Розв'язування систем лінійних рівнянь із двома змінними способом підстановки
Мета: формувати інтуїтивні уявлення про властивості рівносильності системи рівнянь із двома змінними та свідоме розуміння алгоритму розв'язання систем (лінійних) рівнянь з двома змінними, що має назву «спосіб підстановки»; формувати первісні уміння розв'язувати системи рівнянь із двома змінними за алгоритмом «Спосіб підстановки».
Тип уроку: засвоєння знань.
Хід уроку
І. Організаційний момент
- Перевіряємо готовність учнів до уроку та наявність домашнього завдання.
- Повідомляємо місце уроку в темі (тип уроку).
- Розв'язуємо організаційні питання.
II. Перевірка домашнього завдання
Для перевірки домашнього завдання попереднього уроку збираємо зошити — домашню роботу можна оцінити як домашню самостійну роботу або як корекційну роботу наступної самостійної роботи.
III. Мотивація навчальної діяльності
Завдання. Розв'яжіть графічно систему рівнянь 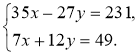
Звісно, застосувавши відомий алгоритм, одразу маємо проблему: побудова або буде неточною 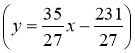 , або точку перетину за відповідного масштабу знайти буде нелегко (дуже великий рисунок). Тому виникає необхідність знайомства з іншим (окрім графічного) способом розв'язування систем рівнянь, які б подолали цю проблему.
, або точку перетину за відповідного масштабу знайти буде нелегко (дуже великий рисунок). Тому виникає необхідність знайомства з іншим (окрім графічного) способом розв'язування систем рівнянь, які б подолали цю проблему.
IV. Актуалізація опорних знань
Виконання усних вправ
-
Чи є розв'язком системи
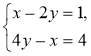 пара чисел:
пара чисел:
1) (-1; 1); 2) (2; -1); 3) (6; 2,5)?
- Виразіть у через х з рівняння:
1) х + у = 2; 2) 2х + у = 2; 3) х + 2у = 2; 4) 2х – 2у = 2; 5) 2х – 3у = 5.
- Розв'яжіть рівняння:
1) ![]() а – 12 = 0; 2)
а – 12 = 0; 2) ![]() ; 3) 0,3у = -6; 4)
; 3) 0,3у = -6; 4) ![]() = 0; 5) 0 · k = 1.
= 0; 5) 0 · k = 1.
-
Серед рівнянь знайдіть пари рівносильних і поясність, чому вибрали їх:
1) х + у = 5; 2) х – у = 5; 3) х = 5 – у; 4) у = х – 5; 5) ху = 5.
V. Вивчення нового матеріалу
l. У радянській школі традиційно, з'ясовуючи зміст рівносильних перетворень рівнянь системи, спирались на графічні ілюстрації. Останнім часом тенденція дещо змінилася — під час обґрунтування перетворень, що передбачені алгоритмами аналітичних способів розв'язування систем (лінійних) рівнянь з двома змінними, на інтуїтивному рівні (на прикладах числових рівностей) вводяться властивості рівносильних перетворень систем k рівнянь з п змінними. Але в будь-якому випадку необхідно, щоб учні усвідомили дві речі, а саме:
1) аналітичні способи розв'язування систем рівнянь є несолідністю, бо найбільша вада графічного способу розв'язування систем рівнянь із двома змінними — це неточність, (а для систем із трьома змінними — неможливість застосування). (Для підтвердження цієї тези можна запропонувати на етапі мотивації відповідний приклад системи);
2) основна мета перетворень, передбачених обома алгоритмами розв'язування систем лінійних рівнянь (підстановки і додавання), — домогтися того, щоб одне з рівнянь системи мало в собі тільки одну змінну.
Звернімо ще раз увагу на те, що доведення властивостей рівносильних систем рівнянь із двома змінними не є (обов'язковою) вимогою, програми з математики.
2. Уведенню алгоритму розв'язання системи лінійних рівнянь із двома змінними передує приклад, у ході розв'язування якого пояснюються основні кроки алгоритму. Тому під час розбору розв'язання цього прикладу треба спеціально зупинитись на етапі вибору тієї змінної, яку будемо виражати із другого (а потім і виключати з іншого) рівняння системи, бо від цього часто суттєво залежить складність перетворень рівняння. Після цього формулювання алгоритму можна подати як коментар до перетворень цього прикладу:
|
Конспект 23 |
|
|
Розв'язування системи лінійних рівнянь із двома змінними способом підстановки |
|
|
Алгоритм |
Приклад: |
|
1. Виразіть з якого-небудь одного рівняння системи одну змінну через іншу |
1. 3 першого рівняння виразимо через х: у = 3 – 2х |
|
2. Підставте в інше рівняння системи замість цієї змінної здобутий вираз |
2. Підставимо в друге рівняння системи замість у вираз 3 - 2х, дістаємо систему:
|
|
3. Розв'яжіть здобуте рівняння з одним невідомим |
3. Розв'яжемо рівняння: 3х – 2(3 – 2х) = 8; 3х – 6 + 4х = 8; 7х = 14; х = 2 |
|
4. Знайдіть відповідне значення іншої змінної |
4. Знайдемо з рівняння у = 3 - 2х значення у при х = 2: у = 3 – 2 · 2 = -1. Відповідь. (2; -1) |
VI. Первинне закріплення
Виконання усних вправ
- Яку змінну зручніше виразити з рівняння?
1) 2х – у = 3; 2) ![]() х + у = 0; 3)
х + у = 0; 3) ![]() ?
?
-
Прокоментуйте, використовуючи алгоритм (конспект 23), хід
розв'язання системи:
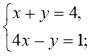
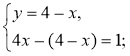
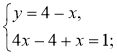
Відповідь. (1; 3).
Виконання письмових вправ
-
Заповніть пропуски так, щоб утворені записи були правильними
(розв'язання системи способом підстановки):
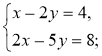
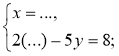
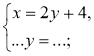
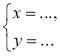
-
Використовуючи алгоритм та приклади, розв'яжіть систему способом
підстановки, перевіривши попередньо, чи має вона скінченну кількість
розв'язків:
1) 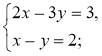 2)
2) 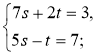 3)
3) 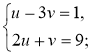 4)
4) 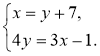
-
Знайдіть координати точок перетину графіків рівнянь, не виконуючи
побудов:
1) х – у = 4 та х + 2у = -2; 2) 5х – у = 10 та 3х – 2у = -8.
-
Знайдіть розв'язки системи рівнянь
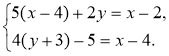
(Звернімо увагу, що перед застосуванням алгоритму бажано записати лінійні рівняння у вигляді ax + by = с.)
VII. Підсумки уроку
Знайдіть «помилку» в розв'язанні:
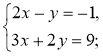
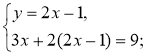
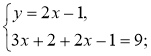
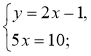
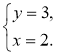
Відповідь. (3; 2).
VIII. Домашнє завдання
№ 1. Вивчіть зміст алгоритму та аналогічно до конспекту «прокоментуйте» розв'язання однієї з таких систем.
№ 2. Розв'яжіть систему способом підстановки:
1) 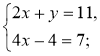 2)
2) 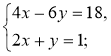 3)
3) 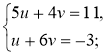 4)
4) 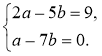
(Перед розв'язанням перевірте, чи дійсно система має єдиний розв'язок.)
№ 3. Відомо, що 2а = b + 1. Виразіть через b:
1) -2a; 2) 4а; 3) 6а; 4) а; 5) 2а + 3.


про публікацію авторської розробки
Додати розробку