Розв'язування систем лінійних рівнянь з двома змінними способом додавання
Тема. Розв'язування систем лінійних рівнянь з двома змінними способом додавання
Мета: закріпити знання алгоритму розв'язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент
- Перевірка готовності до уроку.
- Учитель оголошує план роботи на уроці.
II. Перевірка домашнього завдання
Для того щоб перевірити ступінь засвоєння та свідомого розуміння алгоритму розв'язання систем лінійних рівнянь з двома змінними способом додавання, можна, як і попереднього уроку, організувати роботу в групах (урок № 75) або запропонувати учням самостійно виконати таке завдання.
- Розбийте розв'язання системи на частини, що відповідають алгоритму, і до кожної частини доберіть відповідний коментар:
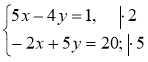
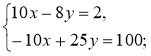
17y = 102; ![]() ; y = 6; 10х – 8 · 6 = 2; 10x = 50; x = 5.
; y = 6; 10х – 8 · 6 = 2; 10x = 50; x = 5.
Відповідь. (5; 6).
-
За складеними коментарями розв'яжіть систему
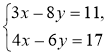 способом додавання.
способом додавання.
Звісно, що по закінченні роботи, учні презентують результати своїх дій та коригують можливі помилки.
III. Формулювання мети й завдань уроку
Мета й відповідні завдання на урок формулюються вчителем разом з учнями, бо зрозуміло (і це можна побачити з перевірки домашнього завдання), що, оскільки з алгоритмом учні познайомились тільки на попередньому уроці, вони ще не досить добре його знають та не дуже досконало ним володіють. Тому основна дидактична (навчальна) мета — закріпити знання алгоритму та відпрацювати його застосування під час розв'язування системи лінійних рівнянь — цілком логічна.
IV. Актуалізація опорних знань
Виконання усних вправ
- Знайдіть НСК чисел: 1) 2 і 3; 2) 2 і 4; 3) 2 і 5; 4) 6 і 9.
- Додайте почленно рівняння системи і розв'яжіть утворене рівняння:
1) 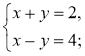 2)
2) 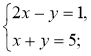 3)
3) 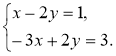
-
Зведіть рівняння до вигляду ах + by – с, де а, b, с — цілі числа, виконавши
рівносильні перетворення рівнянь:
1) 0,1х + 3у = 5; 2) ![]() ; 3) 1,2х + 0,7у = 2,8;
; 3) 1,2х + 0,7у = 2,8;
4) ![]() ; 5) 5(х – 2у) – 1 = 6у + 2.
; 5) 5(х – 2у) – 1 = 6у + 2.
V. Вдосконалення вмінь та навичок
Подальшому засвоєнню змісту відповідного алгоритму сприяє розв'язування вправ, що потребують застосування алгоритму (розв'язування систем лінійних рівнянь саме способом додавання), а навички рівносильних перетворень рівнянь відпрацьовуємо під час розв'язання вправ, що потребують попереднього перетворення рівнянь системи до вигляду ах + by = с. При цьому треба ще раз наголосити, що алгоритми розв'язання систем лінійних рівнянь, розглянуті останнім часом, можуть бути застосовані тільки в тому випадку, якщо система зведена до вигляду 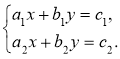
Також бажано на цьому уроці ознайомити учнів зі способом розв'язання нового типу задач — складання рівнянь прямої за двома заданими точками. Цю задачу учні будуть часто зустрічати в курсах алгебри, геометрії та фізики й тому повинні добре її зрозуміти, «впізнавати» її в різних формулюваннях.
Щоб процес відпрацювання навичок не став нудним, підбираємо завдання різноманітного змісту, поширюючи тим самим уявлення про сферу застосування розв'язання систем лінійних рівнянь (див. № 4).
Виконання письмових вправ
- Розв'яжіть систему лінійних рівнянь способом підстановки:
1) 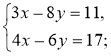 2)
2) 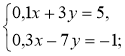 3)
3) 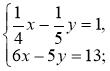
4) 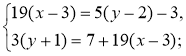 5)
5) 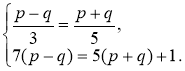
- Пряма y = kx + b проходить через точки А(-2; 1) та В(3; 4). Складіть рівняння цієї прямої.
-
Пара чисел (-2; 3) є розв'язком системи рівнянь
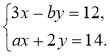 Знайдіть значення а і b.
Знайдіть значення а і b.
4*. Розв'яжіть рівняння:
1) (х – у)2 + (у – 3)2 = 0; 2) (3х – у + 1)2 + (х – 2у)2 = 0.
Перед розв'язанням задачі № 4 необхідно повторити властивість степеня з парним показником та умову, коли сума двох невід'ємних чисел дорівнює 0.
VI. Підсумки уроку
Бажано, щоб на цьому етапі уроку відбулась систематизація знань учнів, тобто, підбивши підсумки виконаних завдань, учні усвідомили:
а) зміст алгоритму розв'язання систем лінійних рівнянь способом підстановки та додавання;
б) місце і значення цього алгоритму під час розв'язування певного виду
завдань.
VII. Домашнє завдання
№ 1. Повторіть зміст алгоритмів розв'язання систем лінійних рівнянь із двома змінними:
а) способом підстановки;
б) способом додавання.
№ 2. Знайдіть розв'язки систем рівнянь найзручнішим способом:
1) 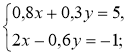 2)
2) 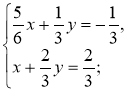 3)
3) 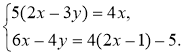
№ 3. Запишіть відповідні рівності:
а) сума чисел х та у в 5 разів більша за їх різницю;
б) добуток чисел а і і на 12 більший за їхню частку;
в) сума чисел х та у становить третину їхнього добутку.
№ 4. Творче завдання. Складіть рівняння прямої, що проходить через дві точки (задайте самі).


про публікацію авторської розробки
Додати розробку
