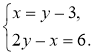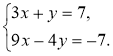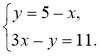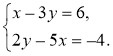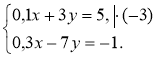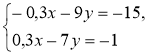Розв'язування систем лінійних рівнянь із двома змінним способом додавання
Тема. Розв'язування систем лінійних рівнянь із двома змінним способом додавання
Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв'язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв'язування систем лінійних рівнянь.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Як перевірку рівня засвоєння знань та вмінь можна дати різнорівневу самостійну роботу, в ході виконання якої перевіряємо вибірково зошити в учнів.
Самостійна робота
Розв'яжіть систему способом підстановки:
|
Варіант І |
Варіант II |
|
А.
Б.
В. Не виконуючи побудови, знайдіть координати точки перетину графіків функцій: |
А.
Б. В. Не виконуючи побудови, знайдіть координати точки перетину графіків
функцій: |
III. Формулювання мети й завдань уроку. Мотивація навчальної діяльності
Для свідомого розуміння необхідності розширення знань учнів щодо способів розв'язування систем лінійних рівнянь, пропонуємо для самостійного виконання.
Завдання. Розв'яжіть систему (відомим вам способом).
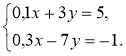
Зрозуміло, що спробувавши: а) побудувати графік; б) виразити одну змінну через іншу (з будь-якого рівняння), маємо певні труднощі (а) неточні побудови; б) незручність обчислень), тому свідомо доходимо висновку про необхідність подальшого вивчення питання про способи розв'язання та їх. застосування під час розв'язування систем лінійних рівнянь із двома змінними (це і є мета й завдання уроку).
IV. Актуалізація опорних знань
Виконання усних вправ
- Знайдіть НСК чисел: 1) 1 і 9; 2) 3; 7; 3) 3 і 6; 4) 6; 15; 5) 2; 5.
- Додайте рівності:
1) а + b = 3 та а – b = 1; 2) 2а – b = 1; 5а + b = 6; 3) 3а + 4b = 1; 3а – 2b = 1.
- Розв'яжіть рівняння:
1) ![]() а – 6 = 0; 2)
а – 6 = 0; 2) ![]() ; 3) 0,5у = -2; 4)
; 3) 0,5у = -2; 4) ![]() = 0; 5) 0 · т = 1; 6) 0 · т = 0.
= 0; 5) 0 · т = 1; 6) 0 · т = 0.
-
Чи проходить через точку М (1; 3) графік рівняння:
1) y = 3x; 2) y = 2x + 1; 3) 5x – 2y = -1; 4) 0 · x + 4y = 13?
V. Вивчення нового матеріалу
Як і в попередній темі, вивченню способу додавання передує приклад, що на числових рівностях показує зміст тих рівносильних перетворень рівнянь системи, що передбачені алгоритмом розв'язування систем способом додавання. Як і на попередньому уроці, зміст самого алгоритму пояснюємо на прикладі. Особливо звертаємо увагу на те, що цей спосіб є більш універсальний, бо для будь-яких значень коефіцієнтів при змінній легко приводить до лінійного рівняння з однією змінною. Також звертаємо увагу на те, що п. 1 в алгоритмі може бути виконаний або повністю (множимо на число обидва рівняння системи), або частково (множимо на число тільки одне рівняння системи).
Записи в зошитах можуть мати вигляд:
|
Конспект 24 |
|
|
Розв'язання систем лінійних рівнянь із двома змінними способом додавання |
|
|
Алгоритм |
Приклад: |
|
1. Помножте обидві частини рівнянь (рівняння) системи на такі числа, щоб коефіцієнти при одній зі змінних стали протилежними числами |
1. помножимо обидві частини 1-го рівняння на (-3); маємо систему:
|
|
2. Додайте почленно ліві й праві частини рівнянь |
2. (-0,3х + 0,3х) + (-9у – 7у) = -15 + (-1) |
|
3. Розв'яжіть здобуте рівняння з однією змінною |
3. -16у = -16; у = 1 |
|
4. Знайдіть відповідне значення іншої змінної |
4. 0,1х + 31 = 5; 0,1х = 2; х = 2 : 0,1; х = 20. Відповідь. (20; 1) |
VI. Первинне закріплення матеріалу
На цьому уроці розв'язуємо велику кількість нескладних вправ, для того щоб виробити стійкі уміння щодо застосування алгоритму.
Виконання усних вправ
Прокоментуйте розв'язання системи рівнянь способом додавання:
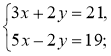
8х = 40; х = 5; 3 · 5 + 2у = 21, 2у = 21 – 15; 2у = 6; у = 3.
Відповідь. (5; 3).
Який крок алгоритму в розв'язанні відсутній? Чому?
Виконання письмових вправ
- Розв'яжіть систему рівнянь способом додавання:
1) 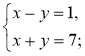 2)
2) 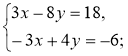 3)
3) 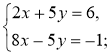 4)
4) 
5)  6)
6) 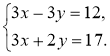
-
Розв'яжіть систему рівнянь способом додавання:
1) 2)
2) 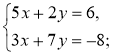 3)
3) 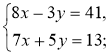 4)
4) 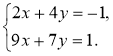
VII. Підсумок уроку
Заповніть пропуски, щоб запис став правильним:
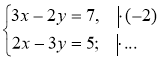
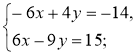
... у = 1; у = ...; 3х – 2 · ...= 7; 3х = ...; х = ...
Відповідь. (...; ...).
VIII. Домашнє завдання
№ 1. Вивчіть зміст способу додавання (розв'язування систем).
№ 2. Розв'яжіть систему рівнянь способом додавання:
1) 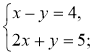 2)
2) 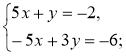 3)
3) 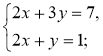 4)
4) 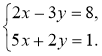
Одну із систем прокоментуйте за алгоритмом (письмово) (див. конспект 23).
№ 3. Чи має розв'язки система рівнянь:
1) 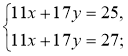 2)
2) 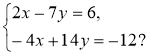
Якщо має, знайдіть хоча б один.


про публікацію авторської розробки
Додати розробку