РОЗВ’ЯЗУВАННЯ СИСТЕМИ РІВНЯНЬ ЗА ДОПОМОГОЮ ГРАФІВ

 

 

 

 

 

 

 

 

 

 

РОЗВ’ЯЗУВАННЯ СИСТЕМИ РІВНЯНЬ ЗА ДОПОМОГОЮ ГРАФІВ

 

 

ЗМІСТ

 

ВСТУП.....................................................…

РОЗДІЛ 1 ОСНОВНА ТЕОРІЯ ГРАФІВ

РОЗДІЛ 2 РОЗВ’ЯЗУВАННЯ СИСТЕМИ РІВНЯНЬ ЗА ДОПОМОГОЮ ГРАФІВ

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ДОДАТКИ

ВСТУП

Перша робота по теорії графів, що належить відомому швейцарському математику Л. Ейлеру, з’явилася в 1736 р. Спочатку теорія графів здавалась досить незначним розділом математики, тому, що вона мала справу в основному з математичними розвагами і головоломками. Проте подальший розвиток математики і особливо її напрямків дав сильний поштовх до розвитку теорії графів. Вже в XIX сторіччі графи використовувалися при побудові схем електричних ланцюгів і молекулярних схем. З іншого боку, ця теорія широко застосовується в різноманітних практичних питаннях: при встановленні різного виду відповідностей, при вирішенні транспортних задач, задач про потоки в мережі нафтопроводів.

Саме з цього часу граф стає однією з найпоширеніших і найпопулярніших математичних моделей у багатьох сферах науки і техніки. Картинка у вигляді набору точок на площині та ліній, проведених між деякими з них, стала зручною і наочною формою зображення найрізноманітніших об’єктів, процесів та явищ.

Великою мірою це пов’язано з виникненням, бурхливим розвитком та поширенням електронних обчислювальних машин і, як наслідок, значним зростанням ролі задач дискретного характеру. Математика від "обслуговування" переважно фізики переходить до проникнення своїх методів у інші сфери людської діяльності. Одним з потужних інструментів такого проникнення є граф.

Із суто формальної точки зору граф можна розглядати як один з різновидів алгебраїчної системи (а саме, як модель), а отже, і всю теорію графів  як розділ сучасної алгебри. Справді, результати та методи алгебри широко використовуються в теорії графів.

Теорія графів тепер застосовується і в таких областях, як економіка, психологія і біологія. Математичні розваги і головоломки також залишаються частиною теорії графів, особливо якщо віднести до них знамениту проблему чотирьох фарб, що інтригує математиків і до цього дня.

У роботові ми розглядаємо деякі прості питання відносно загальної теорії графів; ми вибрали їх так, щоб дати деяке уявлення, з одного боку, про характер досліджень, які можна проводити за допомогою графів, і, з іншого боку, – про деякі конкретні завдання, які можна розв’язувати такими методами.

Актуальність нашої роботи полягає в тому, що на даний момент теорія графів все ширше застосовується в різноманітних сферах нашої життєдіяльності. Зокрема, у фізиці: для побудови схем для розв’язання задач, за допомогою графів значно спрощується розв’язання задач з електротехніки. Архітектори використовують графи для найбільш раціонального розміщення об’єктів і прокладання доріг на плані забудови населеного пункту. Біологи використовують графи для розв’язання задач із генетики. Навіть на математичних заняттях учні використовують графи для розв’язання геометричних задач та задач практичного змісту, для розв’язування системи рівнянь.

Вивчаючи теорію графів, ми поставили таку мету: навчитись застосовувати графи для розв’язування системи рівнянь, тематика яких є актуальною в нинішньому суспільстві.

Також у нашій роботі представлений обширний словник термінів з теорії графів [Додаток А].

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1
ОСНОВНА ТЕОРІЯ ГРАФІВ

 

У основній школі, як правило, розв’язуються системи лінійних рівнянь з двома змінними й окремі види систем лінійних рівнянь із трьома змінними. Розв’язуючи складніші системи лінійних рівнянь способом підстановки або додавання, ми, як правило, змушені виконувати громіздкі перетворення. Інші, раціональніші способи розв’язування систем не вивчаються. Розглянемо один із таких раціональних способів розв’язування систем лінійних рівнянь – спосіб розв’язування їх за допомогою графів. Щоб оволодіти цим способом, треба засвоїти наведені нижче правила побудови й перетворення графів.

Граф – це схема, яка складається з точок і ліній, що сполучають ці точки. Точки називають вершинами або вузлами графа, а лінії – стрілками або вішками. Розрізняють вузли трьох видів: джерела, стоки й прості каскадні вузли. Вузол, із якого вітки тільки виходять, називають джерелом, вузол, в який вітки тільки входять, – стоком. Вузол, який має вхідні й вихідні вітки, називають простим каскадним. Щоб застосовувати графи до розв’язування лінійних рівнянь із кількома змінними або їх систем, домовилися, що вузол графа відповідає змінній, а вітка, що виходить з вузла – коефіцієнту при цій змінній. Кожний вузол характеризується так званим вузловим сигналом х, у тощо, а вітка – передачею вітки а, b, с тощо. Вітку можна побудувати, якщо її передача відмінна від нуля. У противному разі відповідний вузол лишається ізольованим [18, 18].

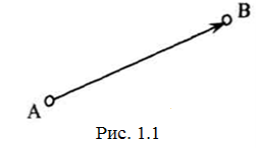
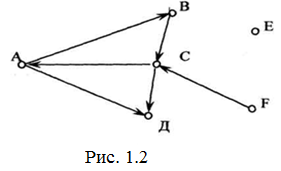
На рисунку орієнтоване ребро зображують стрілкою (рис. 1.1). Говорять, що орієнтоване ребро виходить з вершини А і входить в вершину В. Граф, всі ребра якого орієнтовані, називається орієнтованим графом (рис. 1.2) [13, 92].

Одна і та ж вершина орієнтованого графа може бути початком для одних ребер і кінцем для других. Відповідно розрізняють дві степені вершини: степінь виходу і степінь входу.

Степенем виходу вершини А орієнтованого графа називається число ребер, які виходять з А (позначення: ρ⁺(А)).

Степенем входу вершини А орієнтованого графа називається число ребер, які входять в А (позначення: ρ^–(А)).

Приклад: В графі на рис. 2: ρ ⁺(А)=2, ρ^–(А)=1; ρ⁺(В)=1, ρ^– (В)=1; ρ⁺(С)=2, ρ^–(С)=2; ρ⁺(D)=0, ρ^–(D)=2; р⁺(Е)=0, ρ (Е)=0; ρ⁺(F)=l, ρ^–(F)=0.

В орієнтованих графах будемо розрізняти вершини чотирьох видів [3, 62].

Вершина, у якої степені виходу і входу дорівнюють 0 (ρ⁺=0, ρ^– =0), називається ізольованою. Вершина, у якої степінь виходу більша 0 (ρ⁺>0), а степінь входу дорівнює 0 (ρ^– =0), називається джерелом. Вершина, у якої степінь входу більша 0 (ρ^– >0), а степінь виходу дорівнює 0 (ρ⁺=0), називається стоком. Вершина, у якої і степінь входу і степінь виходу більші 0 (ρ⁺>0, ρ^– >0), називається простою каскадною [18, 28].

На рис. 1.2 вершина Е – ізольована, F – джерело, D – сток, А,В,С – прості каскадні.

Щоб застосувати графи до розв’язування лінійних рівнянь із кількома змінними або їх систем, вважатимемо, що вершина графа відповідає змінній, а ребро, що виходить з вершини – коефіцієнту при цій змінній. Кожна вершина характеризується імпульсом вершини х, у, z, t тощо, а ребро – вагою ребра α, β, γ, ε тощо. Ребро можна побудувати, якщо його вага відмінна від нуля [10, 16].

Кожний вхідний імпульс дорівнює добуткові ваги ребра і імпульсу вершини, з якого це ребро виходить. Ребра, що виходять із вершини, на її імпульс не впливають. Якщо у вершину входить кілька ребер, то її імпульс дорівнює сумі вхідних імпульсів. Розрізняють послідовні і паралельні ребра графа. Якщо початок наступного ребра збігається з кінцем попереднього, то такі ребра називаються послідовними. Ребра, які виходять з одної і тої самої вершини і входять в одну і ту саму вершину, не проходячи через інші, називають паралельними [1, 329].

Кожний вхідний сигнал дорівнює добуткові передачі вітки й сигналу вузла, з якого ця вітка виходить. Вітки, що виходять із вузла, на його сигнал не впливають. Якщо у вузол входить кілька віток, то сигнал його дорівнює сумі вхідних сигналів.

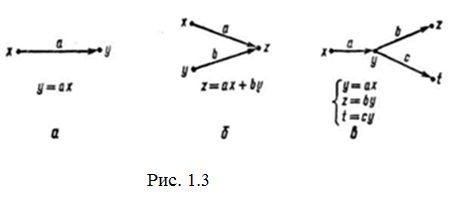
Побудуємо тепер модель лінійного рівняння або системи рівнянь. На рис. 1.3 подано окремі приклади таких моделей. Щоб виключити якусь змінну на графі, треба перетворити відповідний вузол у простий каскадний.

 

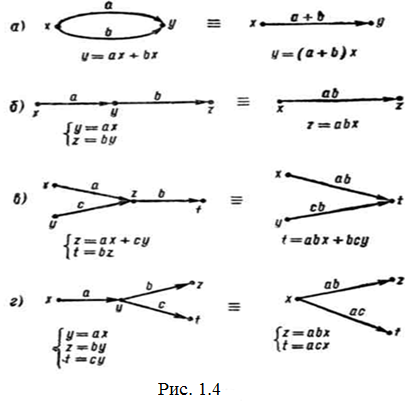
На рис. 1.4 подано основні перетворення графів і відповідні алгебраїчні перетворення рівнянь або систем їх треба розуміти так [16, 14]:

а) дві або кілька паралельних віток можна замінити однією, передача якої дорівнює сумі передач паралельних віток (рис. 1.4, а);

б) дві або кілька послідовних віток можна замінити однією, передача якої дорівнює добутку передач послідовних віток (рис. 1.4, б).

На рис. 1.4 в і 1.4 г показано перетворення послідовних віток графа.

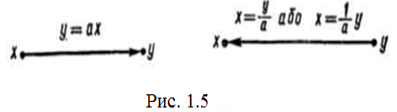
Щоб виразити одну змінну через інші, треба вузол, який відповідає цій змінній, зробити стоком. На рис. 1.5 і 1.6 показано, як змінюється передача кожної вітки при зміні стоку.

Якщо джерело і стік міняються місцями (рис. 1.5), то передача вітки на новому графі виражається числом, оберненим значенню передачі вітки на вихідному.

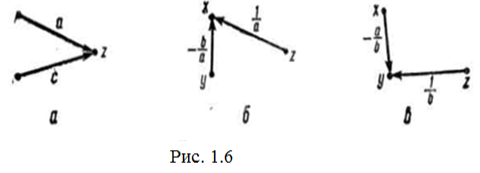
При зміні стоку передача вітки (рис. 1.6, б), яка виходить із того самого джерела, наприклад у, дорівнює добутку числа, протилежного значенню передачі вітки (-b), яка спочатку виходила з цього джерела (рис. 1.6, а), і нової передачі вітки, яка змінила напрям (). Ці висновки можна зробити, побудувавши графи, які відповідають рівнянням

Отже, за допомогою графа одну змінну можна виразити через інші, незалежно від їх кількості.

РОЗДІЛ 2
РОЗВ’ЯЗУВАННЯ СИСТЕМИ РІВНЯНЬ ЗА ДОПОМОГОЮ ГРАФІВ

 

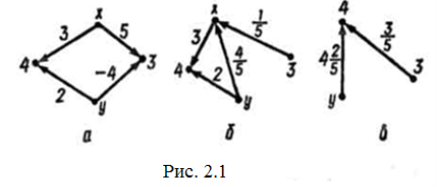
У процесі перетворення графа треба прагнути до поступового перетворення вузлів-джерел у прості каскадні. На мал. 2.1 подано розв’язання за допомогою графів такої системи:

Граф, поданий на рис. 2.1 в, дістали, змінивши послідовні й паралельні вітки графа (рис. 2.1 б) окремими вітками. Розв’язування системи зводиться до розв’язування рівняння першого степеня з однією змінною, яке відповідає графу, зображеному на рис. 2.1 в:

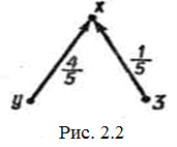
Щоб  знайти х, треба в рівняння, що відповідає графу, поданому на рис. 2.1 б, замість змінної у підставити її значення. Оскільки вітки, що виходять з вузла, на його сигнал не впливають, досить розглянути частину графа, де вузол х є стоком (рис. 2.2), і записати відповідне рівняння: [11, 52].

Відповідь: .

Розглянемо ще один приклад:

 

 

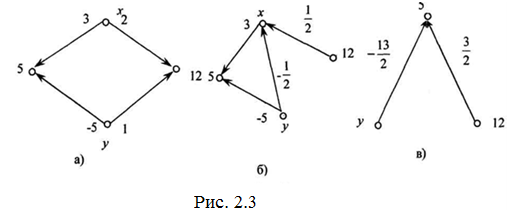
Граф, поданий на рис. 2.3 а, відповідає базовій системі. Граф на рис. 2.3 б, дістали змінивши сток. Вершина-джерело х перетворилась в просту каскадну вершину.

Граф на рис. 2.3 в, дістали, змінивши послідовні й паралельні ребра графа (рис. 2.3 б) окремими ребрами.

Розв’язування системи зводиться до розв’язування рівняння першого степеня з однією змінною, яке відповідає графу, зображеного на рис. 2.3 в: .

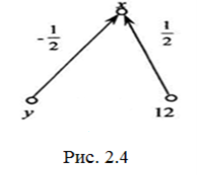
Щоб знайти х, треба в рівняння, що відповідає графу, поданому на рис. 2.3 б, замість змінної у підставити її значення.

Оскільки ребра, що виходять з вершини, на її імпульс не впливають, досить розглянути частину графа, де вершина х є стоком (рис. 2.4) і записати відповідне рівняння: .

Відповідь: (5;2).

Розв’яжемо систему:

На рисунку 2.5 подано її розв’язання:

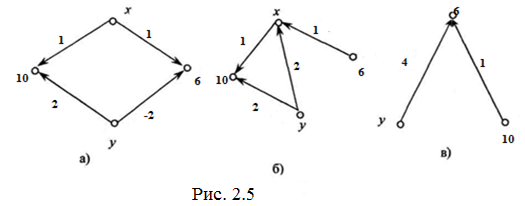
За даними рисунка знайдемо невідомі елементи: .

.

На рис. 2.6 і 2.7 подано розв’язування систем 2 лінійних рівнянь, що не мають розв’язку або мають нескінченну множину розв’язків. Вузол, що відповідає змінній, ізольований від стоку, оскільки передача відповідної вітки дорівнює нулю. Згідно з прийнятими вище домовленостями таку вітку не можна побудувати.

 

 

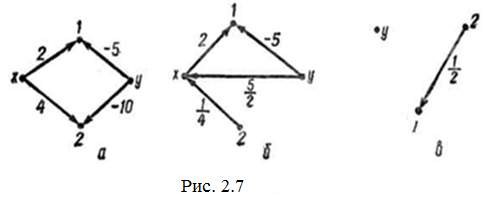
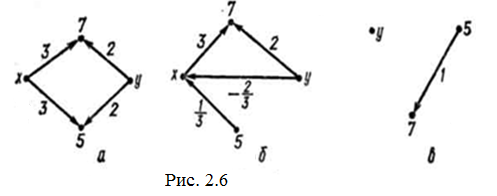
Розглянемо ще приклад такої системи:

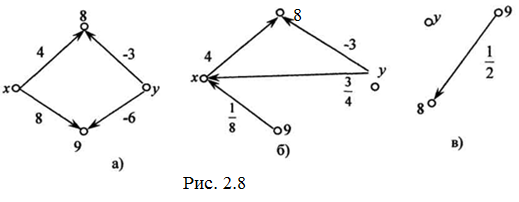
Вершина, що відповідає змінній, ізольована від стоку, оскільки вага відповідного ребра дорівнює нулю. Згідно з прийнятими вище домовленостями таке ребро не можна побудувати.

На рис. 2.8 в ми маємо , це неправильна числова рівність, а отже система розв’язків не має.

Система 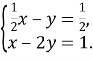розв’язується так:

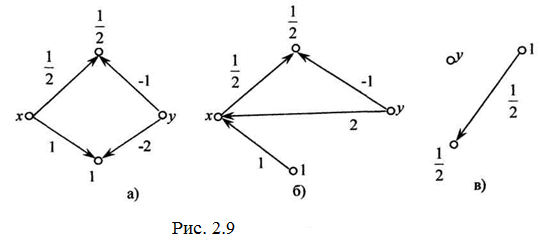
На рис. 2.9 в ми маємо , це правильна числова рівність, і система  має нескінченну множину розв’язків [8].

Рис. 2.10 ілюструє розв'язування системи:

 

 

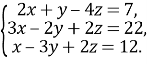
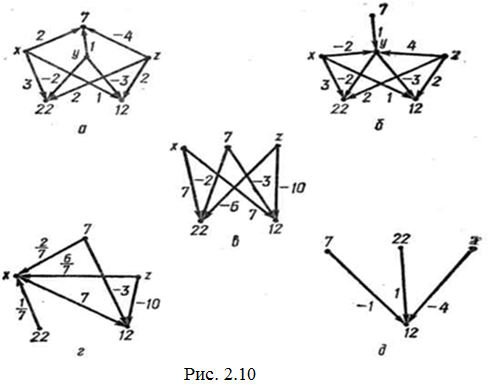
Користуючись цим рисунком

1) встановимо, в якій послідовності виключали змінні, розв’язуючи систему;

2. запишемо рівняння, яке відповідає графу, зображеному на рис. 2.10 д. Знайдемо значення змінної z;
3. значення якої змінної можна знайти, користуючись рис. 2.10 г. Запишемо відповідне рівняння.

Вказівки.

а) До рис. 2.10 д:

б) До рис. 2.10 г:

в) До рис. 2.10 б: .

Відповідь: [7].

 

Розв’яжемо систему трьох лінійних рівнянь з трьома змінними: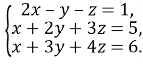

 

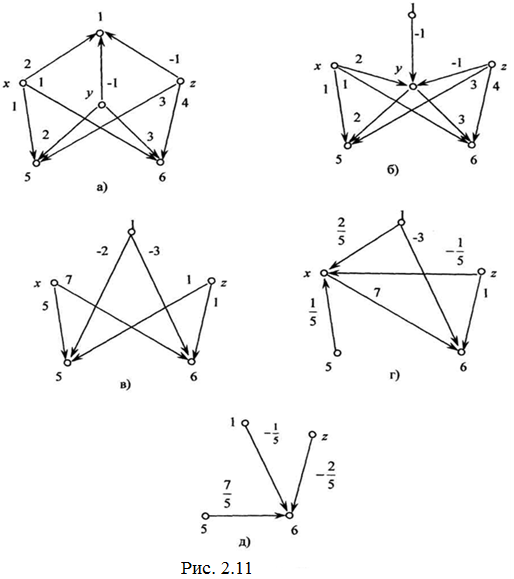
Розв’язування системи зводиться до розв’язування рівняння першого: степеня з однією змінною, яке відповідає графу, зображеного на рис. 2.11 д: [12, 10]

Щоб знайти х, треба в рівняння, значення і записати відповідне що відповідає графу, поданому на рівняння: рис. 2.11 г, замість змінної z підставити її значення і записати відповідне рівняння:

Аналогічно знаходимо у (рис. 2.11 б):

Відповідь: (1;-1;2).

ВИСНОВКИ

У нашій роботі описувались важливі методи, які можуть допомогти розв’язувати системи рівнянь.

Вивчивши основи теорії графів, досліджено розв’язання деяких систем рівнянь за допомогою графів. Розглянуто, як можна використовувати даний метод на практиці.

Дослідження показало, що розглянутий спосіб розв’язування систем лінійних рівнянь:

1.     розвиває творчу активність учнів та формує в них потребу постійно розширювати та поглиблювати свої знання;
2.     розширює математичну культуру учнів і демонструє наявність нетрадиційних підходів до розв’язування математичних задач;
3.     удосконалює прийоми розумової діяльності учнів і розвиває в них дослідницький, творчий підхід до постановки і розв’язування задач у різних сфер людської діяльності.

Працюючи над роботою, ми зрозуміли, що дана тема є актуальною і перспективною в наш час.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.     Акимов О.Е. Дискретная математика: логика, группы, графы, фракталы // «Ульяновский дом печати», 2005, 659 с.
2.     Барболин М.П. Головоломки и графы // Квант, 1975, №2.
3.     Березина Л.Ю. Графи и их применение: Пособие для учителей // М.:Просвещение, 1979, 144 с.
4.     Березина Л.Ю. Графи помогают реишть логические задачи // Математика в школе, 1972, №2, с.62-65.
5.     Березина Л.Ю. О графах с цветними ребрами // Квант, 1973, №8, с. 49-53.
6.     Берж К. Теория графов и ее пременения // М. ИЛ, 1962.
7.     Гарднер М. Математические головоломки и развлечения // М., Мир, 1971.
8.     Генкин С.А., Фомин Д.В. Математический кружок // Санкт-Петербург, 1992.
9.     Головина Л.И. Графы и их применения // Математика в школе, 1965, № 3.
10. Емеличев Л.Ю. Графы и их пременение // М.: Просвещение, 1979.
11. Лисенко В.І. Розв’язування системи лінійних рівнянь за допомогою графів // У світі математики, 1974, № 5, с. 48-56.
12. Мельников О.И. Незнайка в стране графов // Минск, Оракул, 1998.
13. Носов В.А. Комбинаторика и теория графов // МГТУ, 1999, 116 с.
14. Новиков Ф.А. Дискретная математика // Питер, 2001, 104 с.
15. Оре О. Графы и их пременение // М., Мир, 1965.
16. Попов В.М. Дидактика математики: проблеми і дослідження // 2004, Вип.21.
17. Слепкань З.І. Методика навчання математики // К. Зодіак-ЕКО, 2000, 512 с.
18. Уилсон Р. Введение в теорию графов // М., Мир, 1977, 208 с.

                                                      ДОДАТКИ

Додаток А

Словник термінів

Граф. Фігура, що складається з точок (вершин) і відрізків, що сполучають деякі з цих вершин. Сполучаючі відрізки можуть бути прямолінійними або криволінійними; вони називаються ребрами графа.

Дерево. Зв’язний граф, що не має циклів.

Нульовий граф. Граф, що складається тільки з ізольованих вершин: граф, що не має ребер.

Ациклічний граф. Орієнтований граф, що не містить ніякого орієнтованого циклу.

Вершина графа. Або кінець якого-небудь ребра графа, або ізольована точка графа.

Гамільтонова лінія. Елементарний цикл, що проходить по всіх вершинах графа.

Грань багатокутного графа G. Частина площини, обмежена яким-небудь мінімальним циклом G або максимальним циклом C1 графа G; у останньому випадку це частина площини, що лежить поза С1; її називають також нескінченною гранню.

Степінь р(А) вершини A. Число ребер, що сходяться у вершині A. Для орієнтованого графа р(А) означає кількість ребер, що виходять, а р*(А) – кількість вхідних ребер у вершину A; в цьому випадку є два степені.

Ребро графа. Крива, що сполучає дві вершини графа і що не містить інших вершин.

Граф G*, подвійний багатокутному графові G. Багатокутний граф, кожна вершина якого відповідає певній грані графа G, а кожна грань – певній вершині графа G. Дві вершини графа G* сполучено ребром в тому і лише у тому випадку, коли відповідні грані графа G мають загальне ребро.

Дводольний граф. Граф, вершини якого можна розділити на дві непересічні множини так, що вершини однієї і тієї ж множини не сполучені між собою ребрами.

Доповнення G графа G. Граф G+ складається зі всіх ребер (і їх кінців), які необхідно додати до G для того, щоб вийшов повний граф.

Ізольована вершина. Вершина, з якої не виходитиме жодного ребра [18, 22].

Плоский граф. Граф, якого можна накреслити на площині так, щоб його ребра перетиналися тільки в його вершинах.

Ізоморфні графи. Графи G1 і G2 ізоморфні, якщо між їх вершинами можна встановити таку взаємно однозначну відповідність, що пари вершин графа G1 в тому і лише в тому разі сполучені ребром, коли сполучені ребром відповідні пари вершин графа G2. У випадку орієнтованих графів ця відповідність повинна зберігати орієнтацію ребер.

Ікосаедр. Многогранник, обмежений 20 трикутними гранями.

Інцидентність ребра і вершини. Ребро називається інцидентним вершині, якщо вона є одним з його кінців.

Корінь дерева. Будь-яка вершина, яку ми вибираємо за початкову точку дерева.

Кратні ребра. Якщо дві вершини графа сполучено більш ніж одним ребром, то кожне таке ребро називається кратним.

Ліс. Граф. всі зв’язні компоненти якого є деревами (граф без циклів).

Максимальний цикл С1 многокутного графа G. Цикл, що оточує весь граф G.

Мінімальний цикл многокутного графа G. Цикл, утворений граничними ребрами одного з багатокутників, складових G.

Многокутний граф (многокутна мережа) – плоский граф. ребра якого утворюють безліч суміжних, не налягаючих один на одного многокутників.

Непарна вершина. Вершина, степінь якої непарний.

Зворотний граф G* для даного орієнтованого графа G. Граф G* виходить з G через зміну напрямів всіх його ребер.

Однорідний граф степеня r. Граф, степені всіх вершин якого однакові і рівні r

Октаедр. Многогранник, обмежений 8 трикутними гранями.

Орієнтований граф. Граф, на якому вказані напрями всіх його ребер.

Перешийок. Інший термін, для зв’язуючого ребра.

Петля. Ребро графа, обидва кінці якого збігаються.

Повний граф. Граф, будь-які дві вершини якого сполучено ребром. Повний граф, у якого n вершин, має n(n-1) ребер.

Правильний граф. Многокутний однорідний граф, такий, що подвійний до нього граф G* теж є однорідним.

Правильний многогранник. Многогранник, всі грані якого є рівними правильними многокутниками і в кожній вершині якого сходиться однакова кількість ребер.

Зв'язний граф. Граф, кожна вершина якого може бути сполучена деяким ланцюгом з будь-якою іншою його вершиною.

Зв'язуюче ребро. Ребро, видалення якого приводить до збільшення числа зв'язних компонентів графа.

Змішаний граф. Граф, на якому є як орієнтовані, так і неорієнтовані ребра.

Ланцюг. Лінія на графі, що не проходить ні по якому ребру більше одного разу.

Цикл. Замкнутий ланцюг.

Циклічне ребро. Ребро, що не є зв’язуючим.

Цикломатичне число графа G. Кількість ребер графа G мінус число його вершин плюс одиниця.

Граф Ейлера. Граф, що містить ейлерову лінію.

Ейлерова Лінія. Ланцюг, що проходить по всіх ребрах графа в точності по одному разу.

Елементарний ланцюг. Ланцюг, що не проходить ні через одну зі своїх вершин більше одного разу.

Елементарний цикл. Цикл, що не проходить ні через одну зі своїх вершин більше одного разу.