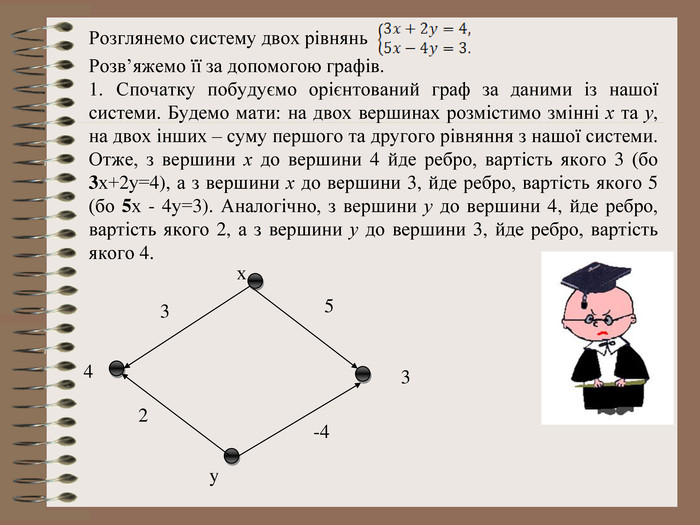
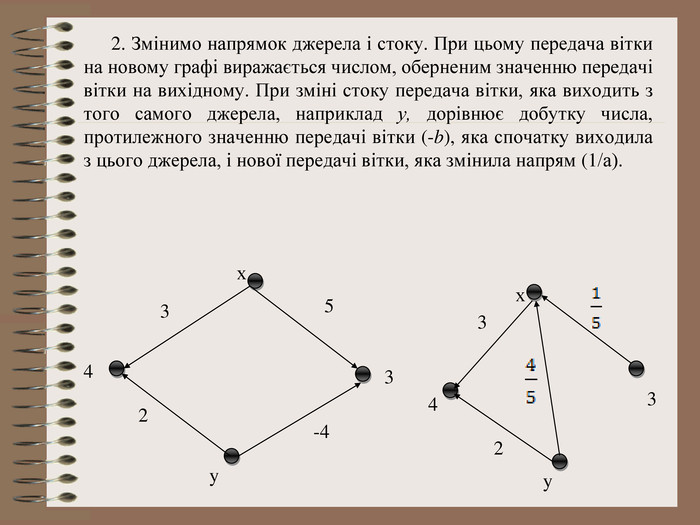
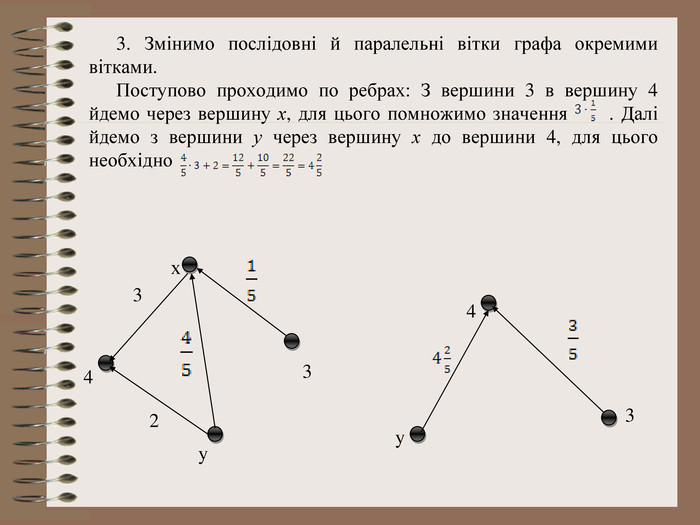
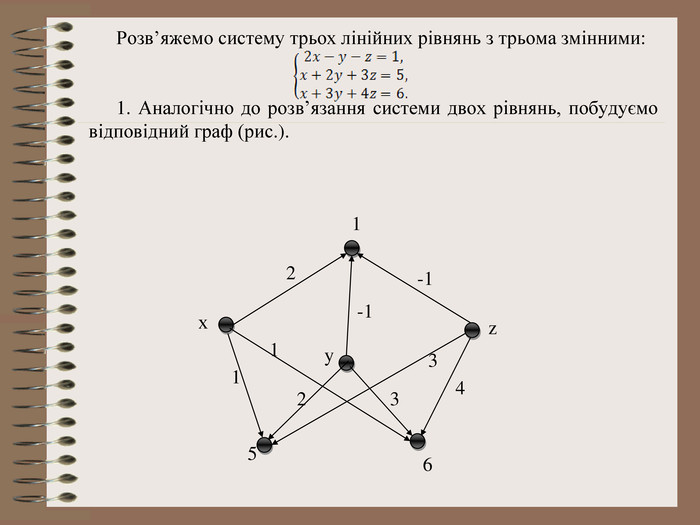
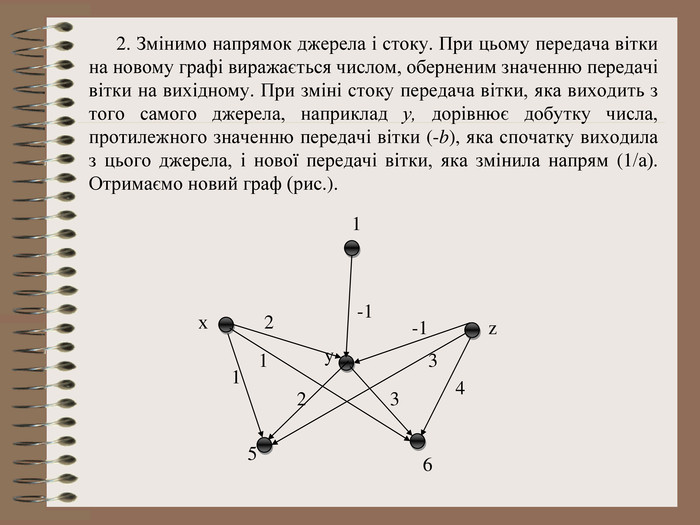
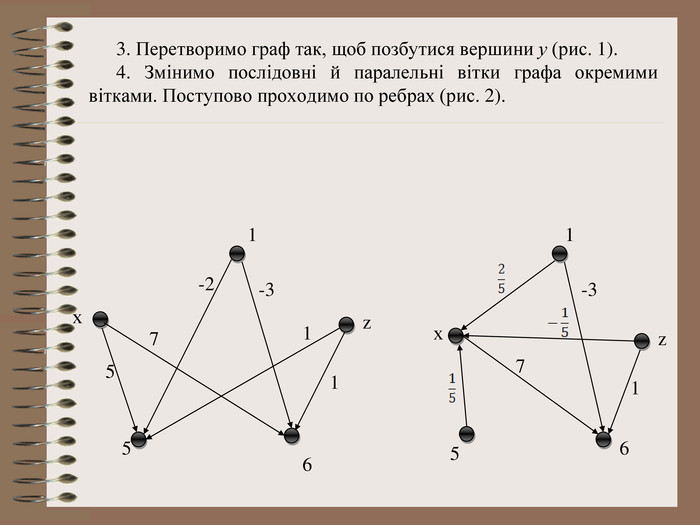
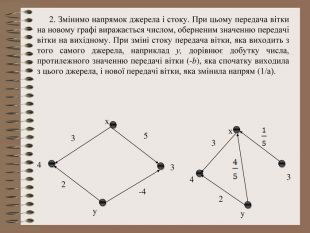
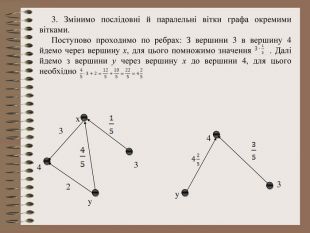
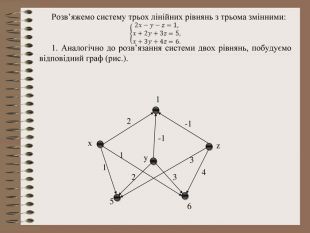
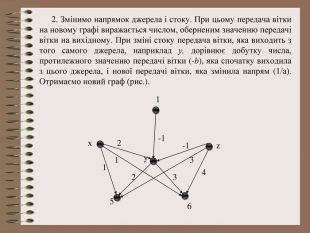
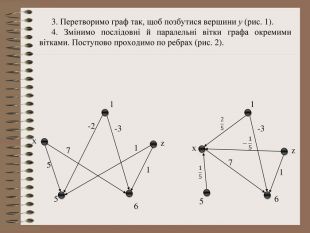
Розв’язування системи рівнянь за допомогою графів

Розв’язування системи рівнянь за допомогою графів

Актуальність: У наш час граф стає однією з найпоширеніших і найпопулярніших математичних моделей у багатьох сферах науки і техніки. Картинка у вигляді набору точок на площині та ліній, проведених між деякими з них, стала зручною і наочною формою зображення найрізноманітніших об’єктів, процесів та явищ. Актуальність нашої роботи полягає у тому, що на даний момент теорія графів все ширше застосовується в різноманітних сферах нашої життєдіяльності.

Історія виникнення графів: Перша робота по теорії графів, що належить відомому швейцарському математику Л. Ейлеру, з’явилася в 1736 р. Спочатку теорія графів здавалась досить незначним розділом математики, тому, що вона мала справу в основному з математичними розвагами і головоломками. Проте подальший розвиток математики і особливо її напрямків дав сильний поштовх до розвитку теорії графів. Вже в XIX сторіччі графи використовувалися при побудові схем електричних ланцюгів і молекулярних схем. З іншого боку, ця теорія широко застосовується в різноманітних практичних питаннях: при встановленні різного виду відповідностей, при вирішенні транспортних задач, задач про потоки в мережі нафтопроводів.

Що ж таке граф?Граф – це схема, яка складається з точок і ліній, що сполучають ці точки. Точки називають вершинами або вузлами графа, а лінії – стрілками. Розрізняють вузли трьох видів: джерела, стоки й прості каскадні вузли. Вузол, з якого вітки тільки виходять, називають джерелом, вузол, в який вітки тільки входять, – стоком. Вузол, який має вхідні й вихідні вітки, називають простим каскадним. На рисунку орієнтоване ребро зображують стрілкою (рис. 1.1). Говорять, що орієнтоване ребро виходить з вершини А і входить в вершину В. Граф, всі ребра якого орієнтовані, називається орієнтованим графом (рис. 1.2).

Моделі рівнянь та системи рівнянь. Побудуємо тепер модель лінійного рівняння або системи рівнянь. На рис. 1.3 подано окремі приклади таких моделей. Щоб виключити якусь змінну на графі, треба перетворити відповідний вузол у простий каскадний.

Щоб виразити одну змінну через інші, треба вузол, який відповідає цій змінній, зробити стоком. Якщо джерело і стік міняються місцями (рис. 1.5), то передача вітки на новому графі виражається числом, оберненим значенню передачі вітки на вихідному.

Основні моменти. При зміні стоку передача вітки (рис. 1.6, б), яка виходить з того самого джерела, наприклад у, дорівнює добутку числа, протилежного значенню передачі вітки (-b), яка спочатку виходила з цього джерела (рис. 1.6, а), і нової передачі вітки, яка змінила напрям (1/а).

Розглянемо систему двох рівнянь. Розв’яжемо її за допомогою графів. Спочатку побудуємо орієнтований граф за даними із нашої системи. Будемо мати: на двох вершинах розмістимо змінні х та у, на двох інших – суму першого та другого рівняння з нашої системи. Отже, з вершини х до вершини 4 йде ребро, вартість якого 3 (бо 3х+2у=4), а з вершини х до вершини 3, йде ребро, вартість якого 5 (бо 5х - 4у=3). Аналогічно, з вершини у до вершини 4, йде ребро, вартість якого 2, а з вершини у до вершини 3, йде ребро, вартість якого 4.хy43352-4

2. Змінимо напрямок джерела і стоку. При цьому передача вітки на новому графі виражається числом, оберненим значенню передачі вітки на вихідному. При зміні стоку передача вітки, яка виходить з того самого джерела, наприклад у, дорівнює добутку числа, протилежного значенню передачі вітки (-b), яка спочатку виходила з цього джерела, і нової передачі вітки, яка змінила напрям (1/а). хy43352-4х3423y

3. Змінимо послідовні й паралельні вітки графа окремими вітками. Поступово проходимо по ребрах: З вершини 3 в вершину 4 йдемо через вершину х, для цього помножимо значення . Далі йдемо з вершини у через вершину х до вершини 4, для цього необхідно х3423y43y

4. Розв’язування системи зводиться до розв’язування рівняння першого степеня з однією змінною, яке відповідає новому графу. Щоб. знайти х, треба в рівняння, що відповідає графу, поданому на 2 рисунку, замість змінної у підставити її значення. Оскільки вітки, що виходять з вузла, на його сигнал не впливають, досить розглянути частину графа, де вузол х є стоком, і записати відповідне рівняння: Отже, отримали результат : х3y

Розв’яжемо систему трьох лінійних рівнянь з трьома змінними:1. Аналогічно до розв’язання системи двох рівнянь, побудуємо відповідний граф (рис.).хy4352-1z311-1261

2. Змінимо напрямок джерела і стоку. При цьому передача вітки на новому графі виражається числом, оберненим значенню передачі вітки на вихідному. При зміні стоку передача вітки, яка виходить з того самого джерела, наприклад у, дорівнює добутку числа, протилежного значенню передачі вітки (-b), яка спочатку виходила з цього джерела, і нової передачі вітки, яка змінила напрям (1/а). Отримаємо новий граф (рис.).хy4352-1z311-1261

3. Перетворимо граф так, щоб позбутися вершини у (рис. 1).4. Змінимо послідовні й паралельні вітки графа окремими вітками. Поступово проходимо по ребрах (рис. 2).х115z75-3-2х175z1-3166

4. Розв’язування системи зводиться до розв’язування рівняння першого степеня з однією змінною, яке відповідає новому графу. Щоб знайти х, треба в рівняння, значення і записати відповідне що відповідає графу, поданому на рівняння: рис. 4, замість змінної z підставити її значення і записати відповідне рівняння: Аналогічно знаходимо у (рис. 2): Відповідь: (1; -1; 2).5z16

Висновки. У нашій роботі описувались важливі методи, які можуть допомогти розв’язувати системи рівнянь. Вивчивши основи теорії графів, досліджено розв’язання деяких систем рівнянь за допомогою графів. Розглянуто, як можна використовувати даний метод на практиці. Дослідження показало, що розглянутий спосіб розв’язування систем лінійних рівнянь:розвиває творчу активність учнів та формує в них потребу постійно розширювати та поглиблювати свої знання;розширює математичну культуру учнів і демонструє наявність нетрадиційних підходів до розв’язування математичних задач;удосконалює прийоми розумової діяльності учнів і розвиває в них дослідницький, творчий підхід до постановки і розв’язування задач у різних сфер людської діяльності.