Розв’язування тригонометричних рівнянь

 

Тема уроку: Розв’язування тригонометричних рівнянь.

Мета:

Навчальна: ознайомити учнів з іншими способами розв'язування тригонометричних рівнянь; навчити раціонально вибирати метод їх розв'язування; удосконалити уміння правильно розв'язувати найпростіші тригонометричні рівняння.

Розвивальна: розвивати навички самоконтролю та взаємоконтролю, логічне мислення, пам’ять, вміння аналізувати ситуацію; творчі здібності та пізнавальну активність.

Виховна: виховувати увагу, активність, інтерес до предмету, правильне математичне мовлення.

Методична мета: конкретизація навчального матеріалу, класифікація і запамятовування вивченого з використанням інтерактивних технологій.

Тип уроку: комбінований (застосування інтерактивних технологій).

Обладнання та наочність: мультимедійний комплекс, таблиці «Значення тригонометричних функцій деяких кутів», «Тригонометричні формули», «Формули для розв’язування найпростіших тригонометричних рівнянь», картки з завданнями, картки самоконтролю, презентація Power Point.

                                                                 Епіграф:                                                   

                                                     Краса і багатство тригонометрії – це її формули. 

Всі вони використовуються при розв’язуванні рівнянь.

 

                                                                Хід уроку

I. Організаційний етап

        Викладач перевіряє готовність учнів до уроку, відмічає відсутніх; роздає учням картки самоконтролю і пояснює  як треба їх заповнювати.

II. Перевірка домашнього завдання.

1. Перевірка завдання, заданого за підручником.

   Перевірити наявність домашніх завдань в зошитах учнів і відповісти на запитання, які  виникли в процесі їх виконання.

2. Самостійна робота з подальшою взаємоперевіркою.

        Викладач нагадує учням, що на минулому уроці були розглянуті види найпростіших тригонометричних рівнянь та  формули для отримання їх коренів, які вони повинні були вивчити на сьогодні.

       Робота по картках. Для перевірки знань учням пропонується письмово на окремих аркушах виконати завдання (слайд № 3). Після його виконання учні  виконують взаємоперевірку за готовими зразками (слайді № 4). Кожна правильна комбінація (відповідність) оцінюється 0,5 бала. Загальна кількість балів за це завдання  вписується до картки самоконтролю.

       Слайд № 3. Знайти відповідність:                                   Слайд № 4.  Відповіді:

               

 

III. Формулювання теми, мети й задач уроку.     

      Мотивація навчальної діяльності учнів

   Притча: З давніх часів, з часів Біблії до нас дійшла притча про трьох сіячів (число 3 символічне своєю триєдиністю – повітря, вода, земля; Бог -отець,Бог-син, Бог –дух святий) Один посіяв зерно при дорозі, інший на камені, а третій вкинув його у родючий грунт. Пройшов час. Зерно при дорозі виросло, але його зламали не достиглим; на камені проросло, але було дуже дрібненьке; на родючому грунті дало гарний врожай.

Отже, ваші знання будуть тоді міцними, коли ви захочете їх взять.

Ви є отим родючим грунтом.

У даний час ви вивчаєте один з розділів математики „ Тригонометрія”, вивчення якого вимагає величезного напруження для осмислення, запам’ятовування  і своєчасного відтворення  ( значна кількість формул).

Цей матеріал виробляє наполегливість,  формує пам’ять  і ось удосконаленню її допоможе розв’язування тригонометричних рівнянь.

Викладач повідомляє   дітям, що тригонометричні функції  застосовуються  також в науці та техніці, тому питання про розв’язування тригонометричних рівнянь досить актуально.  На уроці будуть розглянуті  способи розв’язування тригонометричних рівнянь які зводяться до найпростіших за допомогою тригонометричних формул або винесенням спільного множника за дужки. Кожен учень повинен з’ясувати для себе міру компетентності з метою подальшого відпрацювання теми.

Таким чином на уроці ми маємо систематизувати вже вивчене на попередніх уроках і ознайомитися  з дещо новими міркуваннями, що є важливими при розв’язуванні тригонометричних рівнянь.

        Формулюється тема, мета та епіграф уроку: «Краса і багатство тригонометрії – це її формули. Всі вони використовуються при розв’язуванні рівнянь.» (слайди № 1,2).   

       Викладач пропонує дітям активно попрацювати, бо успіх роботи на уроці буде залежати від праці й внеску кожного з них,   радить  бути уважними, дружними й толерантними.

 

IV. Актуалізація опорних знань

       Учні розбиваються на три групи. Викладач пропонує усно виконати тестові вправи (слайд № 5),  використовуючи метод «Мікрофон», який учні передають із групи в групу. Учень, який дав правильну відповідь, набирає  0,5 бала і записує його до картки самоконтролю.

  Слайд № 5.  Виконання тестових  завдань:

1) Назвати  значення а, при яких рівняння sin t = a  має: а) має один корінь; б) жодного кореня; в) нескінчену множину коренів.

2) Які з наведених тригонометричних рівнянь є найпростішими,  а які ні і чому: а) 2cosx =-1;    б) sin x=1;    в) 4tgx=3;    г) ctg(2x/3)=0 ?

3) Яке з наведених рівнянь не має розв'язків:

    a) sin x=3/7;     б) tg x=5;  в) cos x=5/2;     г) ctg x=-10  ?

4) Коренем рівняння tg x =a  є   t = … .

5) Яка рівність є правильною:

    а)                                  б)                                          в)                                       ?

6) Розв'язати  рівняння sin x=1/2.

    а)                                        б)                                      в)                                г)  

7) Знайти  помилку:

    а)      б)                                              в)                                      г) 

 

V. Засвоєння знань і вмінь

         Викладач нагадує учням, що з шкільного курсу алгебри вони знають, що зведене квадратне рівняння можна розв’язати двома способами: за допомогою дискримінанта  або за теоремою Вієта. Тригонометричні рівняння теж  можна розв’язувати різними способами.  Звертає  увагу дітей на висловлювання: «Якщо результат не залежить від способу розв’язування – це математика, а якщо залежить – це бухгалтерія» (слайд № 6).

         Перед нами стоїть задача – показати знання та вміння з розв’язування тригонометричних рівнянь різних типів (слайд № 7).

 

 

 

 

 

 

 

 

 

 

         Учням пропонується самостійно розв’язати в зошитах  перші три рівняння  з подальшою перевіркою (навички самоконтролю) за готовими зразками (слайд №  8).

 

 

 

 

 

 

        

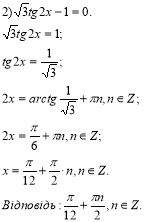
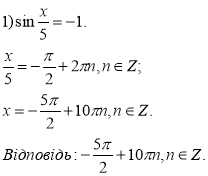
         Відповідь: розв’язків немає. 

Якщо учні  виконали всі три рівняння правильно, то записують до  картки самоконтролю – 3 бали.

 

 

  Проблемні  запитання:

• Чи є наступне четверте рівняння (слайд № 7) найпростішим тригонометричним?
• Як його розв’язати?

  Йде колективне обговорення, після якого рівняння розв’язується учнем

біля дошки (при необхідності з коментарем).

Пошукова  робота.     Далі викладач  пропонує розв’язати рівняння   .

• Як розв’язати це рівняння?
• Чи розв’язували ви колись подібне?

       Учні надають свої пропозиції щодо його розв’язування. Викладач надає можливість учням вибрати один із запропонованих алгоритмів (слайд № 9).

 Слайд № 9. Алгоритм розв’язування рівняння  

1 спосіб:

  З’ясувати чи є дане рівняння найпростішим тригонометричним.

  Застосувати формулу пониження степеня  .

  За допомогою тотожних перетворень звести до найпростішого тригонометричного рівняння.

  Записати відповідь.

2 спосіб:

  Ввести нову змінну sin x = t  і звести дане рівняння до алгебраїчного.

  Пригадати властивості квадратного кореня.

  Розв’язати найпростіше тригонометричне рівняння.

  Записати відповідь.

      Робота в парах. Вибравши алгоритм, учні розв’язують дане рівняння в зошитах. Викладач слідкує за їх роботою. Відповіді учні записують на дошці та порівнюють результати отримані при розв’язуванні різними способами.  Далі діти здійснюють самоконтроль за готовим розв’язанням (слайд № 10, 11). Правильна відповідь  оцінюється в два бали.

 

                                                

 

 

 

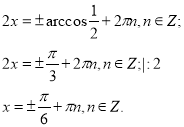
                Відповідь: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Робота в малих групах. 

Для розв’язування наступного рівняння учні об’єднуються в групи (по 4 чол.). 

  Пошукова робота. Викладач надає можливість учням скласти алгоритм одного з способів розв’язування рівняння, використовуючи підказку (слайд № 12)  та розв’язати його.  Записи ведуться на окремих аркушах. Вибір правильного алгоритму – 0,5 бал, правильно розв’язане рівняння  - 2,5 бали.

  Слайд № 12. Скласти алгоритм розв’язування рівняння  двома способами.

  Застосувати формулу синуса подвійного кута.

  Винести спільний множник за дужки.

  За допомогою тотожних перетворень звести до найпростішого тригонометричного рівняння.

  Записати відповідь.

  Добуток дорівнює нулю, якщо хоча б  один із множників дорівнює нулю.

  Застосувати формулу перетворення суми(різниці) тригонометричних функцій у добуток.

  Розв'язати найпростіше тригонометричне рівняння.

        Представники груп записують відповіді на дошці. Перевіряється  розв’язання за готовими зразками (слайд № 13, 14). Учні груп, які отримали правильні відповіді, записують до карток самоконтролю  відповідні бали.

Слайд № 13. Алгоритм розв’язування рівняння   .         

   1-й спосіб:

• Застосувати формулу синуса подвійного кута.
• Винести спільний множник за дужки.
• Добуток дорівнює нулю, якщо хоча б  один із множників дорівнює нулю.
•  За допомогою тотожних перетворень звести до найпростішого тригонометричного рівняння.
• Записати відповідь.

 

      2 – спосіб:

• Застосувати формулу перетворення суми(різниці) тригонометричних функцій у добуток.
• Добуток дорівнює нулю, якщо хоча б  один із множників дорівнює нулю.
• Розв'язати найпростіше тригонометричне рівняння.
• Записати відповідь.

Слайд № 14. Розв’язання рівняння .

              

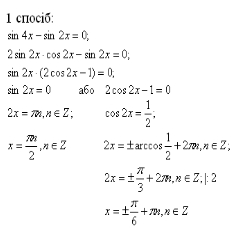
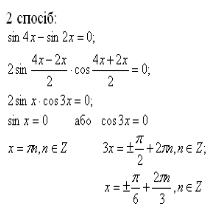
          Далі викладач разом з учнями обговорюють спосіб розв’язування рівняння  . Учні, по черзі, виходять до дошки і записують кожен етап розв’язання (при необхідності його  коментують).

 

VI. Домашнє завдання

     1. Повторити формули для розв’язування найпростіших тригонометричних рівнянь.

     2. Розв’язати рівняння № 8, 9, 4 (застосувати формулу додавання).

     3. Творче завдання. Скласти два тригонометричних рівняння, подібних до № 5, 6. Умову та розв’язання записати на окремих аркушах.

 

 VII. Підсумок уроку

     1. Учні обчислюють кількість балів за картками самоконтролю та віддають їх викладачеві.

     2. Відповідають на запитання, розміщені на слайді № 15:

1)  Про що ви дізналися на уроці?

2)  Які способи розв'язування тригонометричних рівнянь   ви запам'ятали?

3. Під час виконання яких завдань ви відчули труднощі?

 

     3. Рефлексія (слайд № 16).

        Якщо ви не той, хто на вершині, це не значить, що ви той, хто внизу     

       Учні малюють в зошитах ескіз  гори.  Позначають  своє місцезнаходження до вершини гори, яке  відповідає рівню отриманих на уроці знань.  

 

    4. Дякую за співпрацю та старання! (слайд № 17)

 

 

      Картка самоконтролю

 

	Прізвище учня
	Види діяльності	Бали
1.	Робота в парах (взаємоперевірка)
2.	Усне опитування
3.	Розв’язування рівнянь:
	№ 1-3
	№ 5  (робота в парі)
	№ 6 (робота в групах)
4.	Додаткові бали
	Оцінка