«Трансформація зовнішнього і внутрішнього світів Сантьяго у творі П. Коельйо «Алхімік». Стрічка Мебіуса як топологічний символ алхімії»

Біуроки: література і математика

Якщо вірити дослідженням, що проводились на протязі останніх декількох десятиліть в ряді найрозвиненіших країн, IQ в більшості людей не тільки не росте, а навіть зменшується. Дослідники пов'язують це з тим, що люди в загальній масі засвоюють у школах одну і ту ж суму класичних знань. Що відбувається, коли ці знання не трансформувати і пропонувати кільком поколінням підряд в неактуальній формі? Вони перестають дивувати і переходять в ранг рефлексу, а різні дива НТП – в побутову техніку. Ускладнення ж матеріалу, що не відповідає віковим особливостям дітей викличе скоріше відразу, а ніж захоплення знаннями. Наслідком таких кризових процесів у шкільній освіті є те, що вподобання до такого роду знань у більшості дітей падає до нуля. Мозок втрачає свої, вкрай необхідні у навчанні, функції:

• інтерпретувати – будувати всеможливі комбінації із набору елементів/об'єктів;
• відбирати потрібне – інтуїція;
• творити – отримувати нові, корисні об'єкти/предмети.

Хвиля кризових явищ в освіті накрила в тій чи іншій степені всі країни без виключення. Вчителі практики, як найчуттєвіші, давно почали відчувати необхідність змін. У вітчизняній педагогіці неможливо не відмітити уроки В. Сухомлинського – спілкування на природі. Невипадково Юнеско для популяризації досвіду оголосила 2018 рік – роком Сухомлинського. Діти на таких уроках вчаться пізнавати світ у єдності, єдності природи, людини, науки. Будь-який об'єкт/предмет бажано вивчати, розкриваючи його метаморфізм, розглядати з різних боків, збільшуючи вимірність об'єктів. Кроком до якісно нового рівня научіння можуть стати біуроки або сентез-уроки. Вони мають схожі риси з напрямком, що на заході отримав назву STREAM-освіта. Основною позитивною рисою біуроків є творчість, а творчість, породжена інтересом дає розвиток. Окрім того, в цю методику потрібно додати рух – рух по спіралі з елементами реконструкції, та відтворення присутності. Підготовка і проведення таких уроків вимагає якісно нового підходу:

• спільної робота кількох фахівців;
• володіння новітніми засобами навчання.

Пропонуємо для прикладу розробку такого біуроку.

Біурок літератури та математики в 10 класі (2 год.)

Вчителі: Л. Федорова та В. Ловінський

Тема. «Трансформація зовнішнього і внутрішнього світів Сантьяго в романі-притчі Пауло Коельйо «Алхімік». Стрічка Мебіуса як топологічний символ алхімії»

Мета: навчити учнів секулярному сприйняттю твору та топологічних гомеоморфізмів, перетворювати інформацію з однієї форми в іншу; розвивати уяву як основу евристичного методу пізнання; виховувати здоровий інтерес до мультикультурної спадщини людства.

Обладнання: мультимедійне обладнання; набір на кожну парту: аркуш А-4, клей, ножиці.

Є два види подорожніх. Перші можуть ходити тільки по землі.

Другі можуть йти й поводі, але, якщо хоч на мить втратять Віру, то потонуть.

(Із св. письма)

Зміст уроку

І. Дефініція об’єктів вивчення

Організовується пошукова робота в Інтернеті і вибір із всеможливих варіантів найбільш вдалих.

Словник (Вчителі предметними виступають експертами)

Трансформація – зміна, перетворювання виду, форми, істотних властивостей чого-небудь. Езотерика (від грец. ἐσωτερικός — внутрішній) — своєрідний, для непосвячених – містичний погляд на сутність життя, природних процесів. Бачення схованого, незрозумілого для споглядання пересічної людини. Культ таємних знань існував з давніх-давен. Людей, що культивували такі практики, називали жерцями, шаманами, відьмами, екстрасенсами.

Гермес Трисмегіст (грец. Ἑρμῆς ὁ Τρισμέγιστος) — бог у елліністичному Єгипті, який сполучав у собі риси грецького бога Гермеса та єгипетського Тота. Гермесу Трисмегісту приписується авторство герметичної, себто окультної, літератури, доступної тільки для втаємничених: для давніх окультистів навіть «Іліада» та «Одіссея» Гомера фігурували поміж книжками Гермеса Трисмегіста.

Пізніше поняття герметичної літератури та філософії зробилось синонімом алхімії, що намагалася відкрити таємницю перетворення дешевих металів на золото та знайти еліксир довгого, чи навіть безсмертного, життя. З огляду на те, що герметична література була зрозуміла тільки втаємниченим, вважалося, що скарби знання, вкладені в них, Гермес Трисмегіст убезпечив від ока профана магічними печатками. Тому слово герметичність почало означати — щільно замкнений, а герметизм — таємну науку, викладену в тих герметичних книжках.

Алхімік – людина, що займається алхімією.

Алхімія — це загальна назва систем трансформації людини, що засновані на метафорі хімічних перетворень та використанні хімічних сполук, а також спроб отримання дорогоцінних металів, еліксирів, філософського каменю, універсального розчинника, питного золота та інших речовин, які володіють дивовижними властивостями.

Екзотерика — релігійне або філософське вчення, що є відкритим і не являє собою таємниці. Протилежно езотериці (езотеризму) — таємному вченню. Екзотеричне вчення не має глибокого підтексту і зрозуміле всім (загальнодоступне). Екзотеричне (ексотеричне) і езотеричне поняття виникли в давньогрецькій філософії. Зокрема, стародавні дослідники ділили твори Аристотеля на езотеричні і екзотеричні (до них відносилися його діалоги). В західноєвропейській філософії також використовувався такий поділ. Британський філософ Толанд висунув тезу про необхідність двох філософій: екзотеричної (відкритої, публічної) та езотеричної (таємної, для посвячених). Під екзотеричною філософією Толанд мав на увазі релігію, а під езотеричною — матеріалізм.

Іспанський філософ Ортега-і-Гассет в своїй відомій книзі «Бунт мас» говорив про інтелектуальний герметизм масової людини, себто про її щільну закритість небажаним їй ідеям і думкам: «Цей особняк знаходить в своїй духовності репертуар ідей, цілком вироблений (іншими людьми). Він вирішує їх твердо триматися, вважаючи, що йому їх цілком вистачає… Це мірило знаходить у собі ідеї, але не вміє їх творити. Він навіть не підозрює, в якому тонкому оточенні вони витворюються. Він хоче висловити ідею, але не хоче прийняти умови, які потрібні для вироблення думки. І тому його ідеї — тільки бажання, прив'язані до слів… Пересічна людина відчула б себе розгубленою, коли б побачила свою залежність від дискусії з кимсь, — тому вона інстинктивно відкидає цей найвищий трибунал, що знаходиться поза нею…» «Герметизм душі, що не хоче дискусій, кидає маси в так звану безпосередню акцію, що її наказує їм перший-ліпший демагог, який у своїй амбітності, не дбає про те, де правда, а тільки про те, як використати для власної кар'єри інтелектуальний герметизм маси.»

Секуляри́зм (від лат. saecularis — світський) — лояльне ставлення до релігії як такої в суспільстві, родині, політиці тощо. Принцип світськості. Науковий погляд на різні релігії та їх практики, збалансування ролі релігії у політичному, соціальному та особистому житті. Секуляризм не слід плутати із атеїзмом, агностицизмом та індиферентизмом.

Символ (др.-греч. σύμβολον) — походить від двох слів сим і вол, тобто співпадає із суттю. Знак, тощо, який передає сутність чогось іншого.

Діавол – протилежне сутності.

Діалог – навпроти говорити, розмова двох.

Стрічка Мебіуса (німецька вимова [møbiʊs]) є поверхнею лише з однією стороною і лише одним краєм. Вона має математичну властивість неорієнтованості. Також вона є лінійчатою поверхнею. Вона була незалежно відкрита німецькими математиками Мебіусом і Лістінгом 1858 році.

Топологія (грец. τόπος — місце, logos — наука) — розділ математики, який наближений до геометрії. У той час як алгебра починається з розглядання операцій, геометрія — фігур (нерухомих), а математичний аналіз — функцій; найфундаментальніше поняття топології — неперервність. Це геометрія трансформації.

Гомеоморфізм (грец. ομοιο — схожий, μορφη — форма) — в топології, це взаємнооднозначне і неперервне відображення. Простори, зв'язані гомеоморфізмом, топологічно невідмінні (бублик-кружка).

ІІ. Символізм роману «Алхімік» П. Коельйо

Література

Вчитель пропонує найти і прочитати текст із передмови до твору.

1981 року я познайомився зі своїм Учителем, який вивів мене на дорогу, накреслену для мене. І поки він навчав мене своєї науки, я знову повернувся до вивчення алхімії власними зусиллями. Якось увечері, коли ми розмовляли після виснажливого уроку телепатії, я запитав у нього, чому мова алхіміків є такою туманною і такою плутаною.

• Існують три види алхіміків, — сказав мені мій Учитель.

—Ті, котрі висловлюються туманно, бо не знають, про що вони кажуть; ті, котрі висловлюються туманно, бо знають, про що вони кажуть, але вони також знають, що мова алхімії спрямована до серця, а не до розуму.

• А хто належить до третього виду? — запитав я.

Ті, котрі ніколи не чули про алхімію, але в процесі свого життя змогли відкрити Філософський Камінь.

І після тієї розмови мій Учитель — який належав до другого виду — вирішив давати мені також уроки алхімії. Я відкрив, що символічна мова, яка так мене дратувала й так збивала мене з пантелику, була єдиним засобом добутися до Душі Світу або того, що Юнг називав «колективним несвідомим». Я відкрив Персональну Легенду й Знаки Бога, тобто те, що моє інтелектуальне мислення відмовлялося визнати через його простоту. Я відкрив, що досягти Великого Творіння — це не завдання небагатьох, а завдання всіх людських створінь, що населяють поверхню Землі. І є очевидним, що навіть Велике Творіння не завжди постає перед нами у формі яйця та пляшки з рідиною і що всі ми спроможні — поза найменшим сумнівом — поринути в Душу Світу.

Тому «Алхімік» — текст символічний. На його сторінках я не тільки викладаю все, чого навчився з цього питання, а й намагаюся віддати належне великим письменникам, які змогли опанувати Універсальну Мову: Гемінґвею, Блейку, Борхесу (який також використав одну з перських історій для одного зі своїх оповідань), Мальбі Тагану, до речі, теж.

Бесіда-трактування понять з тексту: Алхімія, Душа Світу, Філософський Камінь, Персональна Легенда, Знаки Бога, Велике Творіння. Символізм або метафоричність цих понять і як наслідок –багатогранність. Чи може кожна людина осягнути Мову Світу? Наскільки ми піддаємось загальноприйнятим суспільним нормам? Чи прислухаємось ми до своїх мрій? Їх адекватність?

Математика

Метаматематика символу езотериків.

В пентаграмі (п’ять ліній) (мал. 1, б)) закодовані всі ті поняття, про які згадує автор у передмові: Ім’я Бога, Філософський Камінь, Початок і Кінець, Єдність Природи... Для цього одного уроку непомірно мало. Цей символ містить в собі багато цікавих закономірностей, тому його можна зустріти на емблемах різних організацій, релігій, держав.

Назвіть вам відомі?

Зокрема його ми зустрічаємо у піфагорійців. Зірка – символ «золотого перерізу», здоров’я.

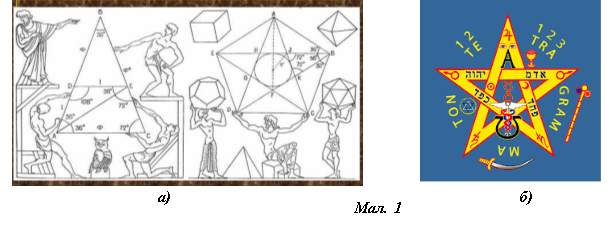
Проаналізуємо за мал. 1, а) трикутник і правильний п’ятикутник як фігури , що містять поділ у

відношенні . В трикутнику або . На пентаграмі серед відрізків HJ, BJ, BH, BE кожен наступний в Ф раз більше попереднього. У такому відношенні знаходяться сторона і діагональ правильного п’ятикутника. Поряд зображені фігури атлетів з правильними пропорціями тіла та його частин – вони знаходяться у відношенні золотого перерізу.

ІІІ. Стрічка Мебіуса і сюжет роману «Алхімік» П. Коельйо

Математика

Проводиться у формі евристичної бесіди.

Що таке поверхня знає кожен. Ми ходимо по поверхні Землі: при грубому наближенні Земля – це куля, а її поверхня – сфера. Дійсна поверхня Землі має різнорівневий рельєф, який на поверхні аркуша паперу в топографії (малювання місця) зображується мапою. Ми звикли до цього перетворення настільки, що воно в нас не викликає подиву. Чи справді аркуш паперу такий звіданий нами?

Розріжемо поздовж аркуш паперу А-4 на 10 стрічок по 2 см.

Склеїмо одну стрічку кільцем. Скільки вона має поверхонь? (дві: внутрішню і зовнішню, проведемо ручкою зовні, а олівцем – всередині)

Так і людина – має зовнішній і внутрішній світи.

Розріжемо кільце посередині по колу. Скільки кілець отримаємо? (два)

Тепер склеїмо одержані кільця одне до одного зовнішніми поверхнями під прямим кутом і розріжемо кожне посередині (мал. 2, а)). Що отримаємо? (квадрат (мал. 2, б)))

Щоб зрозуміти перетворення, з’єднаємо по черзі протилежні сторони квадрата (мал. 2, б) і в)).

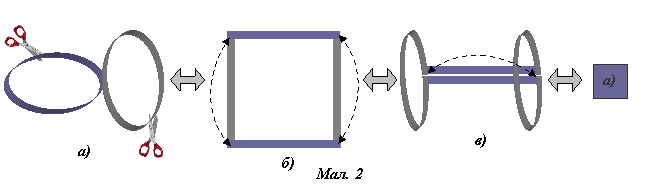
Перетворення, що відбулося, на перший погляд не очевидне.

Продовжимо трансформацію смужок паперу.

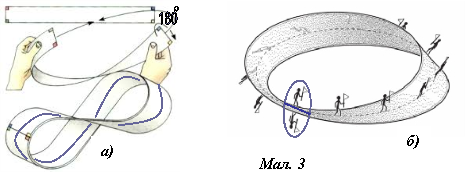
Склеїмо другу стрічку у кільце, але попередньо перекрутивши один її кінець на 180^о – стрічку Мебіуса (мал. 3, а)). Скільки

вона має поверхонь? (одну; проведемо, не відриваючи олівця, лінію – отримаємо замкнену лінію, яка пройде по всій поверхні стрічки)

Стрічка Мебіуса – одностороння поверхня, топологічний об’єкт (наука про місце).

Спробуємо уявити Сантьяго, подорожуючого стрічкою Мебіуса (мал. 3, б)).

Яким буде Сантьяго, коли пройде по стрічці одне коло (два кола)? (дзеркальним відображенням, тим самим?)

Література

Продовження евристичної бесіди, пошук відповідей на питання:

Що відбувається із зовнішнім і внутрішнім світами Сантьяго?

Чи це різні реальності?

Що об’єднує ці реальності?

Як/де/коли об’єднуються зовнішнє і внутрішнє Сантьяго?

Який топологічний об’єкт нагадує шлях Сантьяго у творі?

Чи однаковий Сантьяго на місці розвалин старої церкви на початку і в кінці подорожі?

 

 

Математика

Позначимо на новій стрічці рівномірно цифри від 1 до 5 на одній стороні і від 6 до 0 на іншій. Склеїмо в стрічку Мебіуса.

Прокрутимо стрічку, пропускаючи її між двома пальцями (перед нами пройде послідовність цифр від 1 до 0)

Література

Самостійна робота (в групах та індивідуально – на вибір).

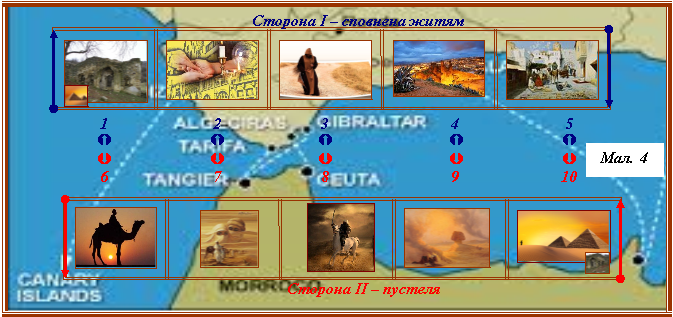
Завдання. Візьмемо нову стрічку. Умовно розбивши на однакові частини з кожного боку (п’ять частин з одного і п’ять з другого боку), позначте (напишіть, намалюйте, створіть презентацію на гаджеті) знаки-символи, які означують кожен з (десяти) етапів подорожі Сантьяго в романі.

Демонструється мапа Середземномор’я.

Приклад символ-стрічки (презентація без детальних коментарів) див. мал. 4.

IV. Дослідницька робота – робота з текстом

Література

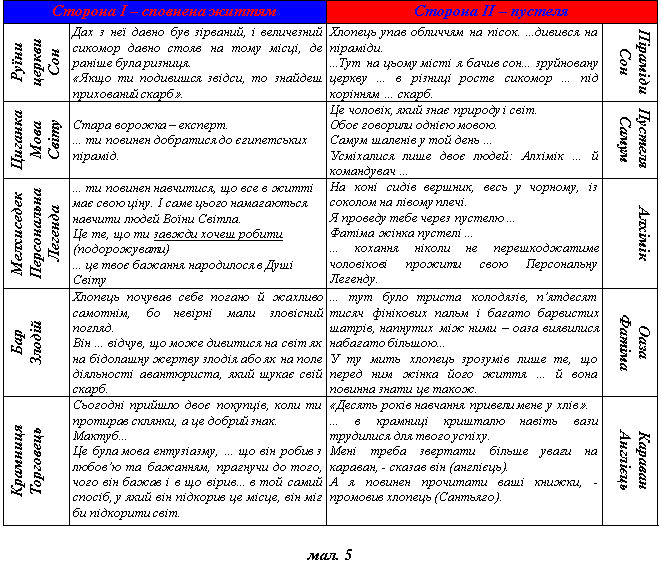
Самостійна робота. Пошук аргументів (цитат), що пояснюють такий поділ стрічки-символа.

Колективна робота. Складання, на основі індивідуальних, єдиної схеми-стрічки (мал. 5).

Математика

Дослідницька робота з трансформації стрічки Мебіуса.

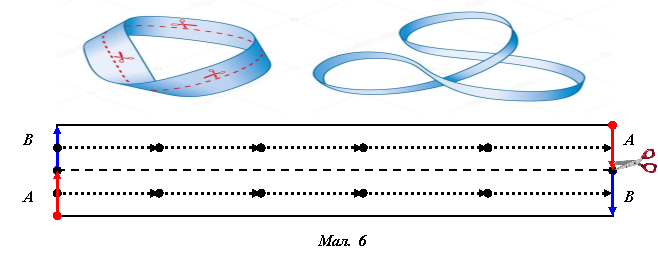
Розріжемо стрічку Мебіуса посередині поздовж. Скільки кілець отримаємо? (одне, довше в два рази вихідного, перекручене два рази, із двома поверхнями – афганська стрічка)

Для пояснення отриманого кільця проаналізуємо мал. 6.

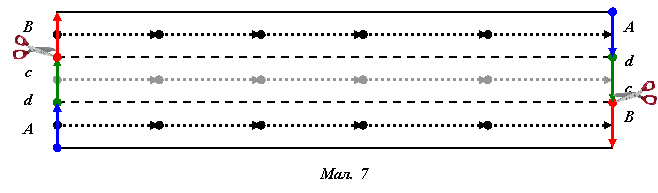
Розріжемо нову стрічку Мебіуса на третину від краю по колу. Скільки кілець отримаємо? (два кільця: одне – довше в два рази, перекручене два рази, із двома поверхнями (афганська стрічка), друге – вужче в три рази (стрічка Мебіуса)).

Один і той же об’єкт може розділитись на два різні топологічні об’єкти з різними властивостями. На мал. 7 схема, що пояснює, як отримуються кільця.

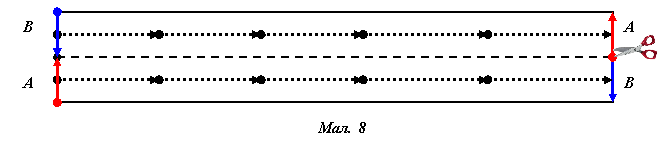
Склеїмо нову стрічку, перекрутивши її один кінець на 360^о (мал. 9, а)). Розріжемо її посередині по колу. Скільки кілець отримаємо? (два однакових кільця, з’єднаних між собою, – афганські стрічки)

Пояснення проводимо, використовуючи мал. 8.

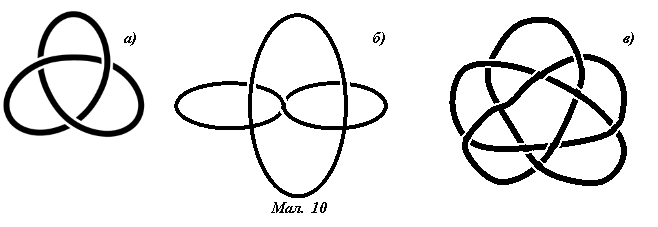
Склеїмо нову стрічку, перекрутивши її один кінець на 540^о (мал. 9, б)), і розріжемо вздовж посередині. Скільки кілець отримаємо? (одне ціле, але скручене у вигляді трилисника – нетривіальний вузол, мал. 10, а))

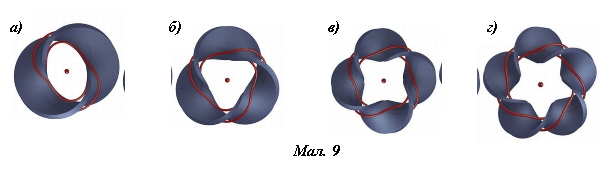
Продовжуємо експериментувати. Склеюємо, перекрутивши один кінець на 720^о (мал. 9, в)), і розрізаємо вздовж посередині. Скільки кілець отримаємо? (два кільця, з’єднаних між собою, формуючи нуль і вісімку мал. 10, б)).

Проробимо для стрічки, скрученої п’ять разів, на 900^о (мал. 9, г)). Скільки кілець отримаємо? (одне ціле, але скручене у вигляді зірки – унікурсальний* граф Ейлера, мал. 10, в)).

* Унікурсальний (латинською – одна дорога) отримується безвідривно від паперу одним розчерком.

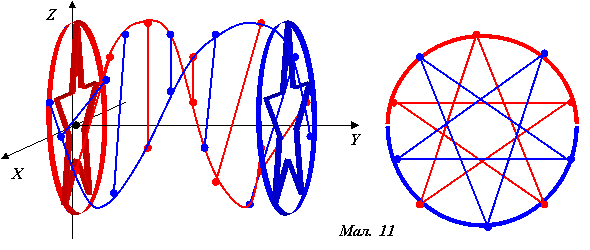
В езотериків така фігура відома як пентаграма. Розглянемо лише деякі цікаві топологічні властивості, що пов’язують зірку в колі і перекручену стрічку (мал. 11). Утворимо конструкцію із двох кілець, що з’єднані між собою двома стрічками на діаметрально протилежних кінцях цих кілець, щось схоже на мал. 2, в), попередньо нанісши на бокові стрічки рівномірно п’ять точок. Коли кільця скручувати в протилежні сторони, то трансформація бокових стрічок покаже знаходження точок на бокових лініях стрічки Мебіуса. Анімацію процесу можна побачити, продемонструвавши частину (з 7.50 до 8.25) відео в YouTube «Кіматика частина 13 ДНК» [https://www.youtube.com/watch?v=ewIUGmeuWI8]

Перекручена стрічка – є лінійчатою поверхнею. Один виток спіралі проектується в коло. Фіксовані відрізки через кожні 36^о проектуються в пряму і перевернуту пентаграму.

V. Застосування набутих знань

Література

«Саме можливість реалізувати сон робить життя цікавішим»

Створити коротку розповідь за сюжетом «Алхіміка», у формі «стрічки Мебіуса», (на реальних своїх або придуманих життєвих моментах) про сон і події, що з ним пов’язані.

Математика

Проблема (спрощений випадок гіпотези Тепліца). Чи в кожну замкнену криву можна вписати прямокутник (мал. 12)?

Для доведення використаємо демонстрацію в YouTube Who cares about topology? (Inscribed rectangle problem) [https://www.youtube.com/watch?v=AmgkSdhK4K8]. Включити режим «звук вимкнено» і коментувати, використовуючи субтитри. Можна провести доведення, використавши малюнки і коментар до них, що запропоновані нижче.

Еліпс, коло, замкнута крива є топологічно еквівалентні або гомеоморфні (подібної форми). Одне трансформується в друге неперервно.

Перефразуємо задачу, використавши ознаку прямокутника: діагоналі рівні і точкою перетину діляться навпіл. Нам потрібно знайти на кривій такі чотири точки, для яких:

AC = BD і AO = BO = CO = DO.

Задамо одну відповідність, взаємнооднозначно і неперервно, між довільною петлею, відрізком і координатною площиною. Таким чином, кожній точці площини відповідають два відрізки з кінцями на петлі. Якщо в квадрата з’єднати сині і червоні сторони, то утвориться тор, кожна точка якого відповідає співвідношенню між довжинами відрізків (мал. 13).

З другого боку, задамо відповідність, взаємнооднозначно неперервно, між довжиною відрізка, розташуванням його кінців на петлі та розташуванням середини в площині x0y і довжиною відрізка по осі 0z. В такому випадку вертикальний відрізок опише поверхню, що нагадуватиме гористий рельєф.

Якщо доведемо, що ці рельєфні поверхні для одного і для другого відрізків перетинаються, то це означатиме співпадання їх середин, а отже існування прямокутника.

Повернімося до площинного прямокутника. Виберемо з кожної пари (х;у) та (у;х) тільки одну. Наш квадрат перейде в трикутник. Трикутник розріжемо навпіл і склеїмо, орієнтуючи бічні сторони від 0 до1. Отримали квадрат. Якщо склеїти його сторони, що розрізалися, враховуючи орієнтацію, то отримуємо стрічку Мебіуса.

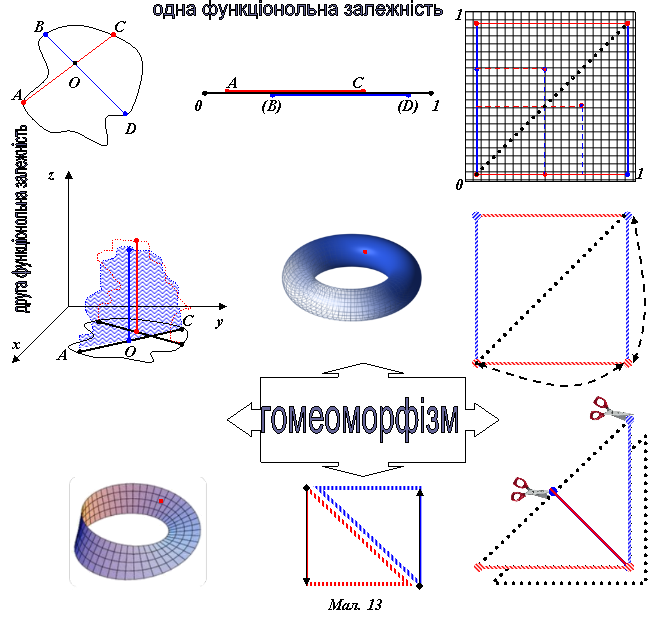
Оскільки ми маємо справу із топологією, то край стрічки сумістимо з петлею на площині x0y, а поверхня стрічки накладеться на рельєфну поверхню і при цьому обов’язково перетне сама себе. А це означає, що для будь-якою довільної петлі існує прямокутник з вершинами на цій петлі.

VІ. Домашнє завдання

Література.

Створити розповідь «Моя Персональна Легенда», спираючись на сюжет роману П. Коельйо «Алхімік».

Математика

Переглянути відео про гіпотезу Тепліца і створити малюнки для доведення її спрощеного випадку із застосуванням топології.