Розв'язування трикутників. Прикладні задачі

Мета:
- закріпити, систематизувати і перевірити знання учнів з теми: «Розв’язування трикутників»; вміння та навички знаходження невідомих елементів трикутника за трьома відомими; уміння застосовувати набуті знання до розв’язування трикутників і прикладних задач; поглибити та розширити діапазон знань учнів з теми;
- формувати навички та уміння практичного використання набутих теоретичних знань, навчити робити облік рівня знань своїх навчальних досягнень, формувати зацікавленість у результатах спільної роботи; розвивати творчі здібності і логічне мислення учнів при знаходженні ними раціональних шляхів для розв’язування практичних задач;
- формувати організаційну, соціально-особистісну, інформаційну, життєтворчу компетентності;
- виховувати прагнення до знань, інтерес до математики, її історії, розглянувши історичні відомості про виникнення тригонометрії як науки, про вклад в розвиток тригонометрії різних вчених-математиків;
- показати застосування тригонометрії в навігації, морехідній астрономії і топографії (профорієнтація: професія судноводія ), показати важливість математичних знань у повсякденному житті , виховувати почуття взаємодопомоги, взаємопідтримки.
Тип уроку: Урок комплексного застосування знань, умінь та навичок учнів.
Форма уроку: Урок - практикум.
Обладнання: картки із завданнями, маршрутні листи, задачі – малюнки, таблиці Брадіса, калькулятори, таблиці-вислови, вимоги до знань та умінь учнів, комп’ютер, презентації, відео «Розв’язування трикутників», проектор, портрети вчених, практичні задачі в малюнках.
Учні повинні знати:
- теореми косинусів і синусів та наслідки з них,
- співвідношення між кутами трикутника і протилежними сторонами.
Учні повинні вміти:
- застосовувати теореми синусів і косинусів та наслідки з них до розв’язування трикутників,
- знаходити невідомі елементи трикутника за трьома відомими,
- застосовувати набуті знання при розв’язуванні прикладних задач.
Математика цікава тоді,
коли живить нашу винахідливість
і здатність міркувати.
Д. Пойа
Хід уроку
І. Організаційний етап.
Організація уваги учнів. Перевірка готовності классу до заняття.
ІІ. Перевірка домашнього завдання.
Збір зошитів.
ІІІ. Оголошення теми та мети уроку.
На попередніх уроках ви розглянули теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників.
Сьогодні перед нами стоїть задача:
- повторити все, що вивчили;
- пригадати те, що забули;
- вміло застосовувати отримані знання до розв’язування геометричних задач.
Незважаючи на те, що попереду у нас велика пізнавальна робота, я сподіваюсь, що ми зможемо зберегти гарний настрій до кінця уроку, а якщо вдасться, то ще його й покращимо.
Але перш, ніж ми почнемо я прошу звернути вашу увагу на «Пам’ятку для учнів». Ознайомтесь, будь-ласка, із запропонованими вам рекомендаціями. Якщо ви будете слідувати їм, то я впевнена, що сьогодні на уроці ви обов’язково виконаєте всі завдання тільки на високому рівні.
Справжній скарб для людини – вміння трудитися.
Езоп
Пам’ятка для учнів.
- Будь уважним.
- Міркуй, шукай, порівнюй, роби висновки, працюй.
- Шукай нові способи розв’язування проблеми.
- Самостійно встановлюй зв’язки відомого з невідомим.
- Будь наполегливим і не бійся помилитися.
- Експериментуй та виправляй невдалі спроби.
- Будь упевнений у своїх здібностях.
Тож давайте познайомимося з планом маршруту нашого уроку.
Маршрутний лист уроку
|
Прізвище, ім’я учня |
|
|
Теоретичний бліц-турнір (правильна відповідь – 1 бал) |
|
|
Математичний диктант (правильна відповідь – 1 бал) |
|
|
Спіймай помилку (правильна відповідь – 1 бал) |
|
|
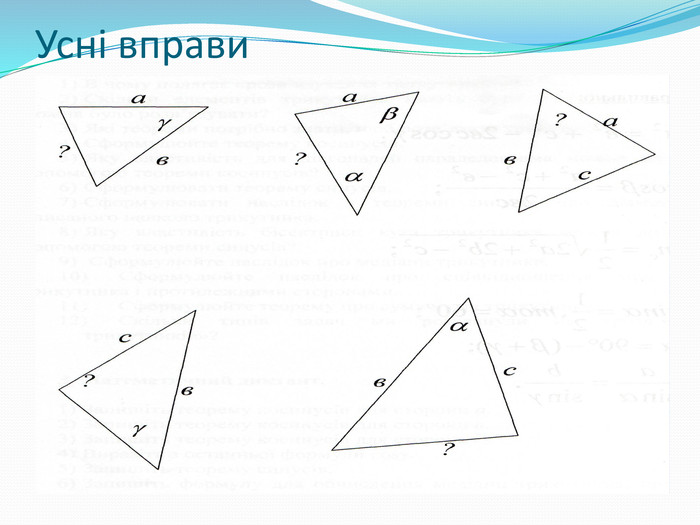
Усні вправи (правильна відповідь – 1 бал) |
|
|
Прикладна задача (повний розв’язок – 3 бали) |
|
|
Історичне дослідження (презентація – 2 бали) |
|
|
Кросворд (правильна відповідь – 1 бал) |
|
|
Всього балів: |
|
Цей лист вказує кроки уроку та їх оцінка. Тому ви самі фіксуете свої бали а в кінці уроку підібʼємо підсумки.
ІV. Мотивація навчальної діяльності.
Математика застосовується абсолютно скрізь. Зараз математика застосовується не тільки в астрономії, механіці, фізиці, хімії і техніці, де вона застосовувалася і раніше, але також – у біології, суспільних науках і навіть у мовознавстві. Математики передбачають погоду, обчислюють орбіти штучних супутників, курси кораблів, перекладають наукові тексти з однієї мови на іншу.
Знання стають міцнішими, якщо вони застосовуються у практичній діяльності.
Тому проведемо урок практичного застосування знань, що ви отримали під час вивчення теми «Розв’язування трикутників» і ви дізнаєтеся як можна застосувати знання даної теми в житті.
ІV. Актуалізація знань, умінь та навичок.
Епіграфом до нашого уроку буде висловлювання Блеза Паскаля:
«Серед рівних розумом – за однакових інших умов – переважає той, хто знає геометрію».
- Теоретичний бліц-турнір.
Учитель зачитує запитання, учні відразу відповідають. Неправильні відповіді виправляють самі учні (і лише за необхідності – вчитель). За правильні відповіді учні виставляють у маршрутний лист кількість набраних балів.
Перелік запитань
- В чому полягає «розв’язування трикутників»?
- Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?
- Які теореми потрібно знати, щоб розв’язати трикутник?
- Сформулюйте теорему косинусів.
- Яку властивість для діагоналей паралелограма можна довести за допомогою теореми косинусів?
- Сформулювати теорему синусів.
- Сформулювати наслідок з теореми синусів про діаметр кола, описаного навколо трикутника.
- Сформулюйте наслідок про медіани трикутника.
- Сформулюйте наслідок про співвідношення між кутами трикутника і протилежними сторонами.
- Сформулюйте теорему про суму кутів трикутника.
- Скільки типів задач ми розглянули на «розв’язування трикутників»?
Другий крок «математичний диктант» за рисунком
- Математичний диктант.
- Запишіть теорему косинусів для сторони а.
- Запишіть теорему косинусів для сторони в.
- Запишіть теорему косинусів для сторони с.
- Виразіть з останньої формули соsγ.
- Запишіть теорему синусів.
- Запишіть формулу для обчислення медіани трикутника, проведеної до сторони а.
7) Запишіть, чому дорівнює квадрат сторони СМ трикутника СDМ.
8) Запишіть рівності, що випливають з теореми синусів для OLK:
9) Який кут трикутника найбільший, якщо його сторони а=7, в=9, с=5?
10) Відомо, що сторона а трикутника менша за кожну з двох інших сторін. Який кут трикутника найменший?
(Учні, що сидять за однією партою, міняються зошитами та виконують взаємоперевірку. Правильні відповіді записані заздалегідь на закритій частині дошки.)
3.Метод «Спіймай помилку».
Неправильно:
-
.
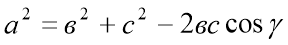
-
.
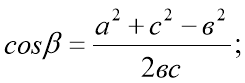
-
.
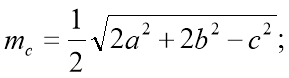
-
.
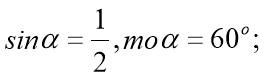
-
.
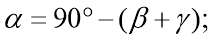
-
.
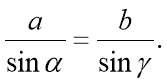
V. Застосування знань, закріплення вмінь і навичок при розв’язуванні задач.
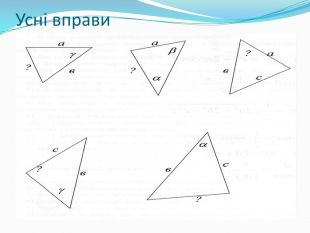
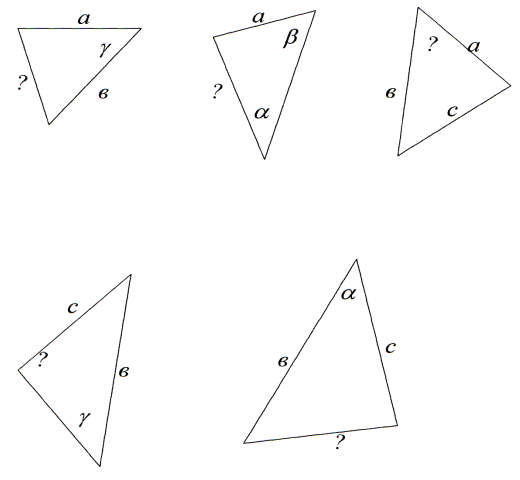
1. Усні вправи.
Розв’язування задач за готовими малюнками, де потрібно знайти невідомі елементи трикутників за готовими малюнками, які проектуються на екрані.
2. Історичні дослідження учнів.
Теорема Піфагора – перше твердження, яке пов’язувало довжини сторін прямокутного трикутника. Згодом люди дізналися, як вимірювати довжини сторін і величини кутів гострокутного і тупокутного трикутників. Виникла наука «тригонометрія» («тригон» – по грецьки означає «трикутник»). Ця наука широко використовується в життєвих ситуаціях, а саме: для вимірювання висоти предмета, вимірювання відстані до недоступної точки.
Учні заздалегідь готують історичні повідомлення:
- Причини зародження тригонометрії. Перші кроки тригонометрії.
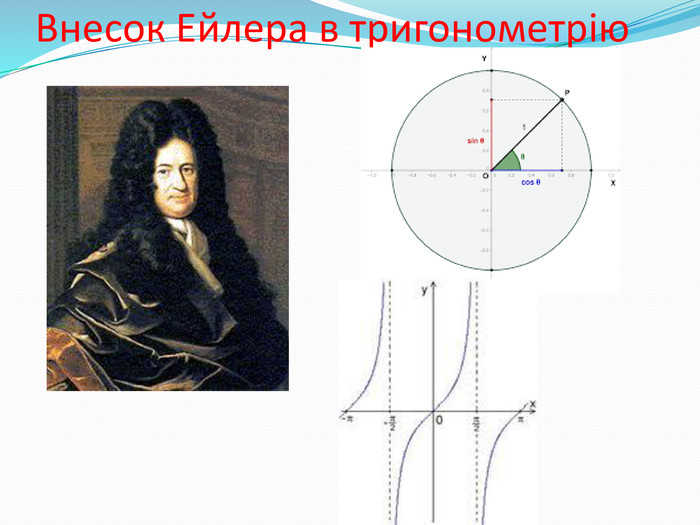
- Вклад вчених в розвиток тригонометрії. Внесок Ейлера в тригонометрію.
Матеріали для рефератів учнів:
- Причини зародження тригонометрії.
Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька
подорожей інший італієць – Америго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.
Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.
Створити все це неможливо було без точного математичного розрахунку. Для виконання цих розрахунків елементарної геометрії Евкліда часто не вистачало. Необхідні були нові способи, нові методи в математиці, і, зокрема, в геометрії.
Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, а розвиток астрономії був неможливий без розвитку тригонометрії.
Перші кроки тригонометрії
Слово “тригонометрія” складається із двох грецьких слів: “триганон” – трикутник і “метрайн” – вимірювати. У буквальному значенні “тригонометрія” означає “вимір трикутників”.
Астрономія, а разом з нею і тригонометрія виникли і розвивалися в народів з розвиненою торгівлею і сільським господарством: у вавілонян, греків, індійців, китайців. Зародилася вона багато століть тому. Про це ми можемо не тільки здогадуватись.
В одному з китайських рукописів, що був написаний близько 2637 року до н.е., є відомості з астрономії, де застосовуються обчислення тригонометричного характеру.
Вавилоняни вже на початку III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру.
Велике значення для розвитку тригонометрії в період її зародження мали праці грецьких учених.
Протягом тисячі років тригонометрія була підсобною наукою у астрономії.
Складалися нові таблиці, знаходилися нові залежності між тригонометричними функціями, за допомогою яких розв’язувалися складні задачі, але тригонометрія залишалася тільки частиною астрономії, самостійної науки не існувало.
- Вклад вчених в розвиток тригонометрії.
У IX – XV ст. на розвиток тригонометрії великий вплив зробили народи, що населяли територію теперішніх середньоазіатських країн, країн Закавказзя, Іраку, Афганістану і Сирії.
Аль – Хорезмі (IX ст.) систематизував індійські таблиці тригонометричних величин.
Абуль – Вефа (940 – 998рр) склав таблиці синусів через кожні 10 мінут.
Вінцем досягнень середньоазіатських вчених у галузі тригонометрії можна вважати відділення її від астрономії і виокремлення в самостійну науку. Головна заслуга в цьому належить азербайджанському вченому Насиреддіну Тусі (1201 – 1274рр). У його праці ми вперше зустрічаємо доведення теореми синусів і теореми тангенсів.
У складанні тригонометричних таблиць видатних успіхів досяг узбецький вчений з м. Самарканда Аль – Каші (помер близько 1430р.). Він обчислив таблиці синусів з точністю до однієї мільярдної. Це були найточніші таблиці на той час.
Німецький математик Йоган Мюллер (1436 – 1476) першим з європейських учених дав послідовний виклад тригонометрії , обчислив дуже точні таблиці синусів і тангенсів.
Багато для розвитку тригонометрії зробили й інші вчені. Завдяки праці кількох поколінь учених тригонометрія стала самостійною наукою.
![C:\Documents and Settings\Papa\Local Settings\Temporary Internet Files\Content.IE5\M1F56TYS\MCj04133020000[1].wmf](/uploads/files/624626/134007/145668_html/images/var-www-naurok-com-ua-web-uploads-files-624626-134007-konspe.010.png)
Внесок Ейлера в тригонометрію.
Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям
Леонарда Ейлера.
Заняття астрономією, географією і морехідними науками неможливі без застосування тригонометрії. Але до початку XVIII ст. вона була наукою неопрацьованою, часто незручною в роботі, що іноді призводило до помилок. Це змусило Ейлера переглянути доведення тригонометричних формул. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С.
Ейлер розробив тригонометрію як науку про тригонометричні функції.
У працях Ейлера тригонометрія набула сучасного вигляду. На підставі його робіт були укладені підручники з тригонометрії, що викладають її в строгій науковій послідовності.
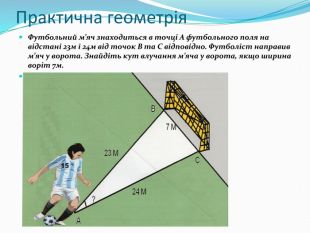
3. Практична геометрія.
Розв’язування задач фронтально, з коментуванням
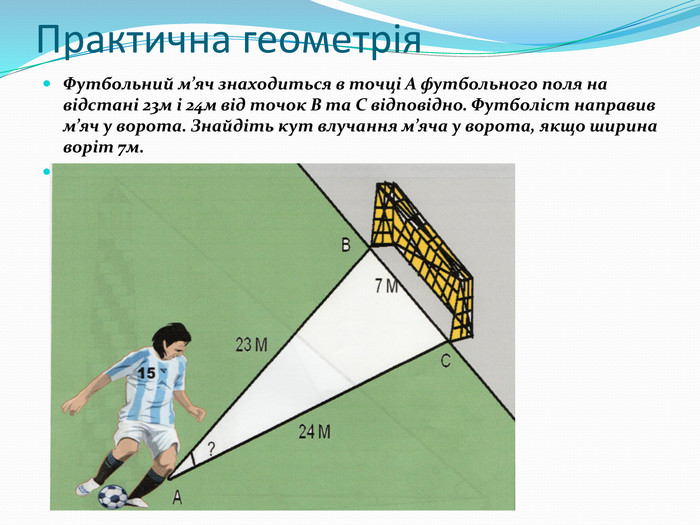
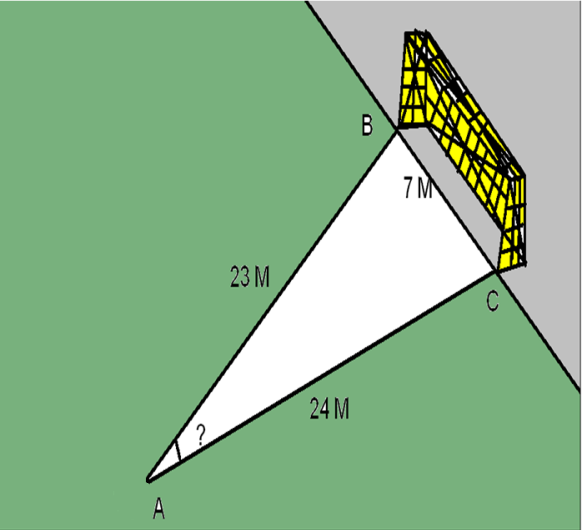
1.Футбольний м’яч знаходиться в точці А футбольного поля на відстані 23м і 24м від точок В та С відповідно. Футболіст направив м’яч у ворота. Знайдіть кут влучання м’яча у ворота, якщо ширина воріт 7м.
![C:\Documents and Settings\Doom\Local Settings\Temporary Internet Files\Content.IE5\GH7WBEGN\MC900440359[1].png](/uploads/files/624626/134007/145668_html/images/var-www-naurok-com-ua-web-uploads-files-624626-134007-konspe.012.png)
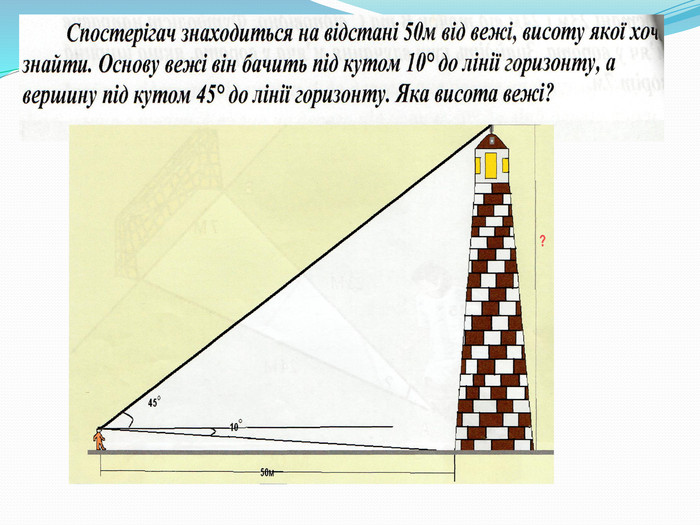
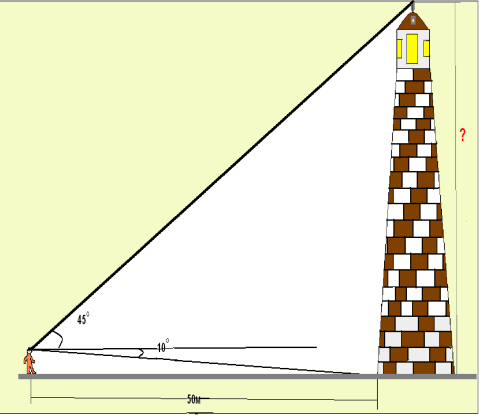
2.Спостерігач знаходиться на відстані 50м від вежі, висоту якої хоче знайти. Основу вежі він бачить під кутом 10° до лінії горизонту, а вершину під кутом 45° до лінії горизонту. Яка висота вежі?
. Розповідь вчителя про професію судноводія (штурмана).
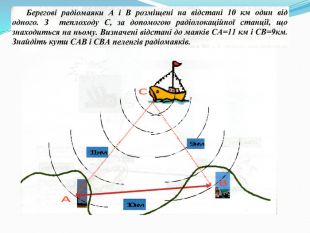
Широко використовується тригонометрія в професії судноводія.
Штурман, судноводій, навігатор в перекладі з латинської – людина, «що може ходити по морю», «їздити по морю». В давнину судноводії приводили кораблі в потрібне місце, користуючись найпримітивнішими засобами. Тому довгий час основними районами плавання залишались прибережні. В плавання, як правило, вирушали влітку, коли небо було безхмарним, вдень світило сонце, а вночі були добре видні зірки. Перша згадка про морські карти відноситься до 490 р. до н.е. Вони були дуже примітивними і скоріше нагадували креслення. Потреба мореплавців у плаваннях далеко від берегів поставили питання про подальше вдосконалення морських карт, морехідних приладів, видвинули на перший план проблему астрономічних спостережень. Тому важливим кроком став винахід інструмента для визначення висоти світил – астролябії (Х ст.).
В ХІІ ст. в Європі з’явився магнітний компас. В XV ст. була винайдена лінійка Герсона- кутомірний прилад, який був більш точним, ніж астролябія.
Застосування цих приладів здійснило революцію в навігації. За допомогою них мореплавці могли орієнтуватися в будь-яких районах Світового океану. Почалася епоха великих
географічних відкриттів. Великі морські плавання значно збагатили науку і вплинули на подальший розвиток астрономії, навігації, топографії – основних складових науки про судноводіння.
Навігація вирішує питання визначення напрямів і пройденої відстані в морі; методи обчислення шляху і способи визначення місця судна в морі по береговим і плавучим
орієнтирам за допомогою штурманських приладів; питання керування і безаварійної проводки судна при особливих умовах плавання.
Морехідна астрономія вирішує питання визначення місця судна в морі за положенням небесних світил.
Картографія допомагає за допомогою теорії картографічних проекцій, що застосовується в судноводінні, розв’язувати аналітичними і графічними способами специфічні штурманські задачі по проведенню судна з врахуванням дії різних факторів( вітру течії і т.д.).
Всі ці науки побудовані на строгій математичній основі. Але конкретні обставини на морі, інколи дуже складні, не завжди дозволяють штурману отримати необхідну інформацію з потрібною точністю навіть за допомогою сучасних технічних засобів. Тому судноводіння, побудоване на науково-математичній основі, забезпечує безпеку судна при плаванні в будь-яких умовах.
Уміння здійснити плавання найзручнішим в даних умовах шляхом, найбільш точно провести судно в порт призначення, з необхідною точністю визначити місце судна в морі практично на будь-яких відстанях – все це залежить від судноводія. І всі ці задачі вирішуються з застосуванням знань з тригонометрії.
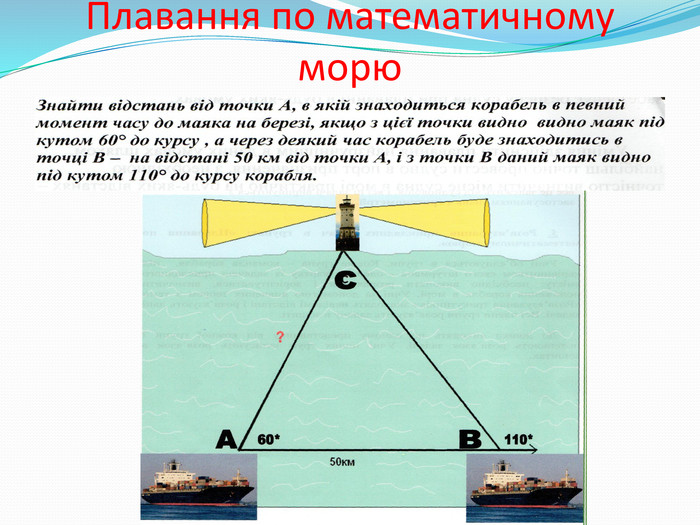
5. Розв’язування прикладних задач в групах: «Плавання по математичному морю».
1 група

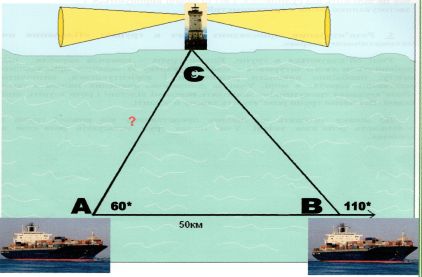
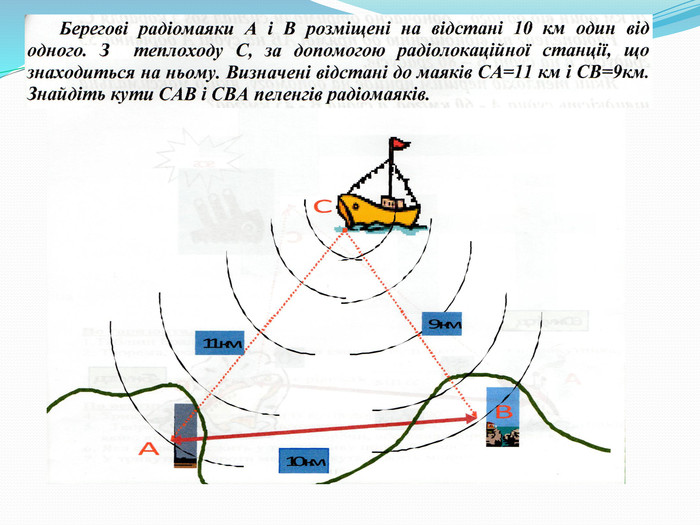
2 група


VІ. Закріплення знань, умінь і навичок.
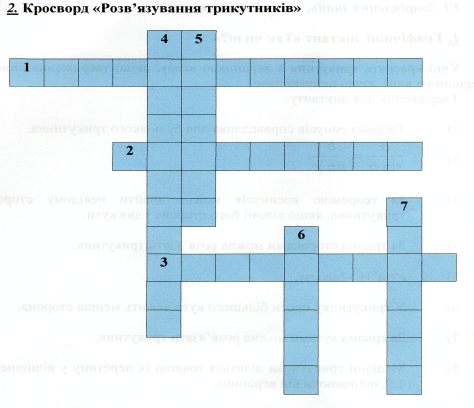


Розв’язати задачу – значить знайти і пройти шлях, що веде до знаходження очікуваної відповіді.
Під час розв’язування прикладних задач зрозуміло яку велику роль грає математика в житті.
Математичні знання потрібні не тільки тим, хто присвятить себе науковій діяльності, але й тим, хто стане займатись практичними справами.
Математика потрібна і в побуті, і в техніці, і на виробництві
VІІ. Підсумок уроку.
- Виставлення і коментування оцінок.
Учні оголошують свої результати.
2.Метод «Чотири ЩО?»
- Що ви дізналися, навчилися на уроці?
- Що сподобалося найбільше?
- Що було найскладнішим?
- Що треба ще вивчити?
VІІІ. Домашнє завдання.
Повторити § 11-13 . Скласти і розв’язати 1-2 практичні задачі на розв’язування трикутників.
ІХ. Рефлексія.
Метод «Похвали себе».
Учні вказують на позитивні сторони своєї роботи на уроці.



про публікацію авторської розробки
Додати розробку