Розв'язування задач на застосовування теореми косинусів і наслідків з неї.

Тема уроку. Розв'язування задач на застосовування теореми косинусів і    

                       наслідків з неї.

Мета уроку: формування вмінь учнів застосовувати теорему косинусів і наслідки з неї до розв'язування задач.

Тип уроку: комбінований.

Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника» [13], посібник [14].

Вимоги до рівня підготовки учнів: застосовують теорему косинусів до розв'язування задач.

Хід уроку

І. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та від­повісти на запитання, які виникли в учнів при їх розв'язуванні

Розв'язування задач

1. c² = a² + b² – 2abcosγ; с² =144 + 64 – 2 ∙ 12 ∙ 8 ∙ 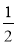= 208 – 96 = 112;
   с =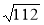 10,6.

a² = b² + c² – 2bccosα; 144 = 64 + 112 – 2 ∙ 8 ∙ 10,6cosα; 169,6cosα = 32;

cosα 0,19; α 79°.

Тоді β = 180° - α - γ 180° - 60° - 79° = 41°.

Відповідь. с = 10,6, α 79°, β 41°.

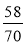
2. a² = b² + c² – 2bccosα; 16 = 49 + 25 – 70cosα; 70cosα = 58; cosα =0,829; α 34°.

b² = a² + c² – 2accosβ; 25 = 16 + 49 – 56cosβ; 56cosβ = 40; cosβ = 0,714; β 44°.

Тоді γ = 180° - α - β 180° - 34° - 44° = 102°.

Відповідь. α 34°, β 44°, γ 102°.

3. Нехай у трикутнику ABC АВ = с, AC = b. BC = a (рис. 15).
   Проведемо висоту CD (два випадки).

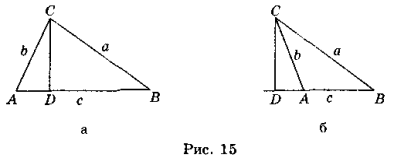
За наслідком із теореми косинусів маємо:

а² = b² + с² ± 2с np_cb = b² + c² ± 2c ∙ AD. Звідси AD = .

Із трикутника ACD за теоремою Піфагора маємо:

CD = = = .

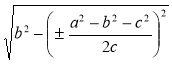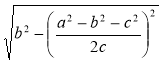Відповідь. .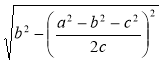

ІІ. Самостійна робота

Самостійну роботу навчального характеру можна провести, скориставшись посібником [14], тест 2 «Теорема косинусів та її наслідки».

III. Формування вмінь і навичок учнів

Застосування теореми косинусів

Користуючись теоремою косинусів, можна довести кілька важливих теорем.

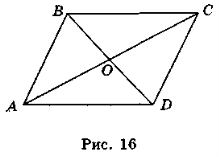
Наприклад: сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін.

Доведемо цю теорему, використовуючи теорему косинусів.

Нехай ABCD — паралелограм, AB = CD = a, AD = BC = b, AC = d₁, BD = d₂ (рис. 16).

За теоремою косинусів із трикутника ABD маємо:

BD² = AB² + AD² – 2 ∙ AB ∙ AD ∙ cosA,

= a² + b² – 2abcosA.         (1)

За теоремою косинусів із трикутника ABC маємо:

АС² = АВ² + ВС² – 2 ∙ AB ∙ BC ∙ cosB, або

АС² = АВ² + ВС² – 2 ∙ АВ ∙ ВС ∙ cos(180°- A),

АС² = АВ² + ВС² + 2 ∙ АВ ∙ ВС ∙ cosA, = a²+ b² + 2abcosA.   (2)

Додавши рівності (1) і (2) почленно, одержимо: + = 2(а² + b²), що і треба було довести.

Розв'язування задач

1. Сторони паралелограма дорівнюють 23 см і 11 см. Знайдіть діагоналі паралелограма, якщо вони відносяться як 2 : 3. (Від­повідь. 20 см і 30 см.)
2. Діагоналі паралелограма дорівнюють 12 см і 14 см, а різни­ця сторін становить 4 см. Знайдіть сторони паралелограма. (Відповідь. 7 см і 11 см.)
3. Дві сторони трикутника дорівнюють 7 см і 11 см, а медіана, проведена до третьої сторони, дорівнює 6 см. Знайдіть третю сторону.

Розв'язання

Нехай у трикутнику ABC (рис. 17) АВ = 7 см, ВС = 11 см, BD — медіана (AD = DC), BD = 6 см.

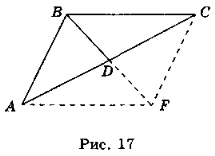
Продовжимо медіану BD і відкладемо на продовженні відрі­зок DF так, що DF = BD. Чотирикутник ABCF — це паралелограм (оскільки діагоналі АС і BF точкою перетину діляться навпіл), тоді AC² + BF² = 2 ∙ (AB² + BC²).

Звідси AC² + 12² = 2 ∙ (7² + 11²), тоді АС² + 144 = 340; АС² =196; АС = = = 14 (см).

Відповідь. 14 см.

4. Доведіть, що в опуклому чотирикутнику сума квадратів діа­гоналей у 2 рази більша від суми квадратів відрізків, які спо­лучають середини протилежних сторін.

Доведення

Нехай у чотирикутнику ABCD (рис. 18) AN = NB, BF = FC, CK = KD, DM = = AM. Оскільки NF = MK= AC, MN = KF = BD і чотирикутник MNFK — паралелограм, то, скориставшись теоремою про суму квадратів діагоналей паралелограма, маємо: NK² + MF² = 2(MK² + MN²) = 2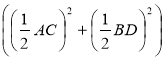=     = (AC² + BD²) або AC² + BD² = 2 ∙ (NK² + MF²), що і треба було довести.

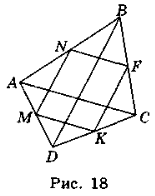
5. За трьома сторонами а, Ь, с трикутника ABC знайдіть його медіани т_а, т_b, т_с (т_а, т_b, т_с —медіани, проведені до сто­рін а, b, с відповідно).

Розв'язання

Нехай у трикутнику ABC (рис. 19) ВС = а, АС = b, АВ = с, АК — медіана, АК = т_а. Продовжимо медіану АК так, що AK = KD. Тоді ABDC — паралелограм, у якому діагональ AD = 2m_a. Оскільки сума квадратів діагоналей паралелогра­ма дорівнює сумі квадратів усіх його сторін, то AD² + BC² = 2(AC² + + АВ²). Звідси (2т_а)² + а² = 2(b² + с²). Із останньої рівності знаходимо, що т_а: т_а = .

Міркуючи аналогічно, знаходимо медіани т_b і т_с:

т_b = ; m_с = .

Відповідь. т_а = ; т_b = ; т_с =

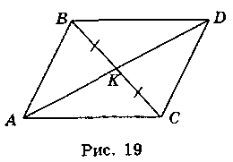
6. За трьома медіанами т_а, т_b, т_с трикутника ABC знайдіть його сторони a, b, c (т_а, т_b, т_с — медіани, проведені до сто­рін а, b, с відповідно).

Розв'язання

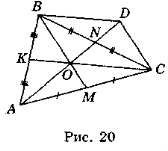Нехай у трикутнику ABC AN = m_a, ВМ = т_b, СК = т_с (рис. 20). Позначимо довжини сторін, які треба знайти, та­ким чином: ВС = а, АС = b, АВ = с. Продовжимо одну із медіан, напри­клад AN, так, що ON = DN. Сполучимо точку D із точками В і С, одержимо паралелограм BOCD, у якого сума ква­дратів діагоналей дорівнює сумі квадра­ тів його сторін, а саме: ВС² + OD² = 2(ОВ² + ОС²) (1). Підставимо в формулу (1): ВС = а, OD = т_а, ОВ = т_b, ОС = т_с, одержимо:

.

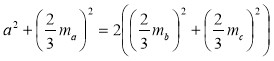Звідси знаходимо а: =.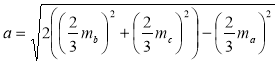

Міркуючи аналогічно, одержимо формули для сторін b і с:

b = ; с = .

Відповідь. a = ; b = ; с = .

IV. Домашнє завдання

Розв'язати задачі.

1. Дано паралелограм з діагоналями с і d і кутом α між ними. Знайдіть сторони паралелограма.
2. Знайдіть медіани трикутника, сторони якого дорівнюють 5 м, 6 м і 7 м.

V. Підбиття підсумків уроку

Завдання класу

1. Сформулюйте теорему про суму квадратів діагоналей пара­лелограма.
2. Діагоналі паралелограма дорівнюють 2 см і 2 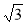см, а кут між ними становить 30°. Визначте, які з наведених тверджень є правильними, а які — неправильними.

а) Сторона паралелограма, що лежить проти кута в 30°, до­рівнює 1 см.

б) Менша діагональ утворює з меншою стороною паралело­грама кут у 120°.

в) Сума квадратів усіх сторін паралелограма становить 20 см².

г) Більша сторона паралелограма дорівнює см.