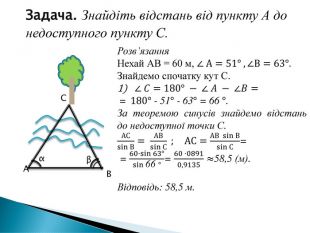
Розв'язування трикутників. Прикладні задачі
Про матеріал
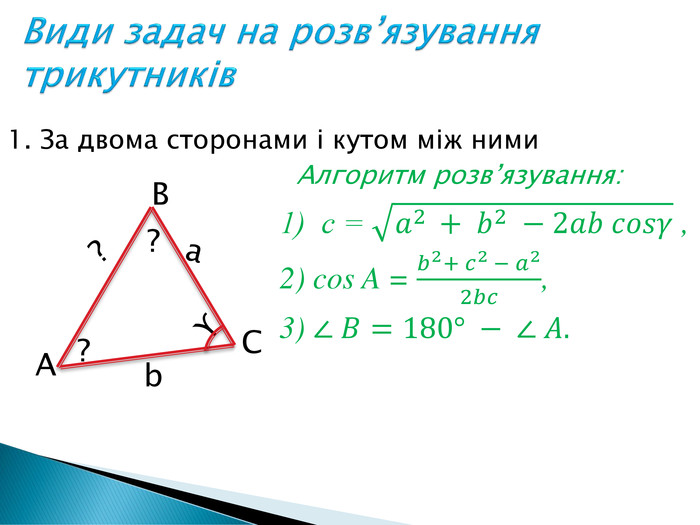
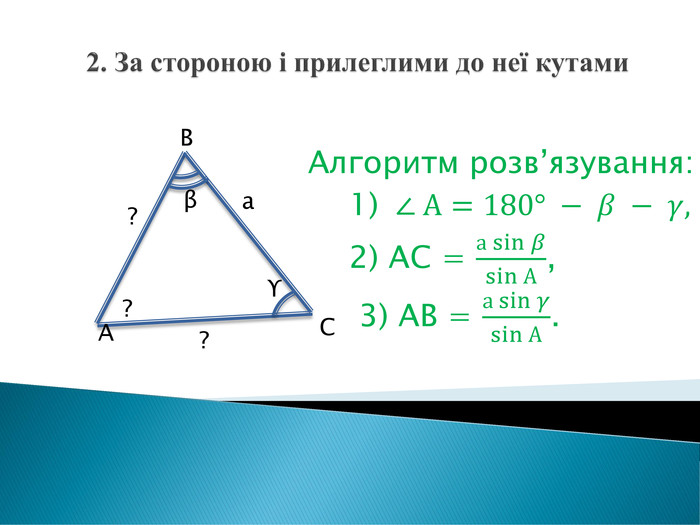
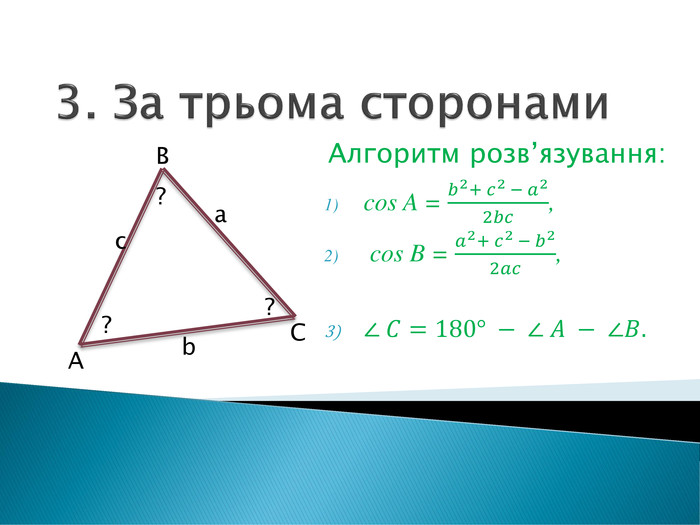
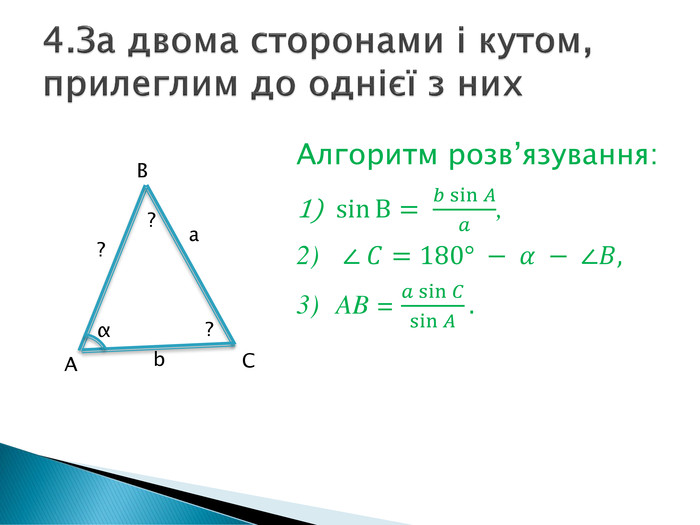
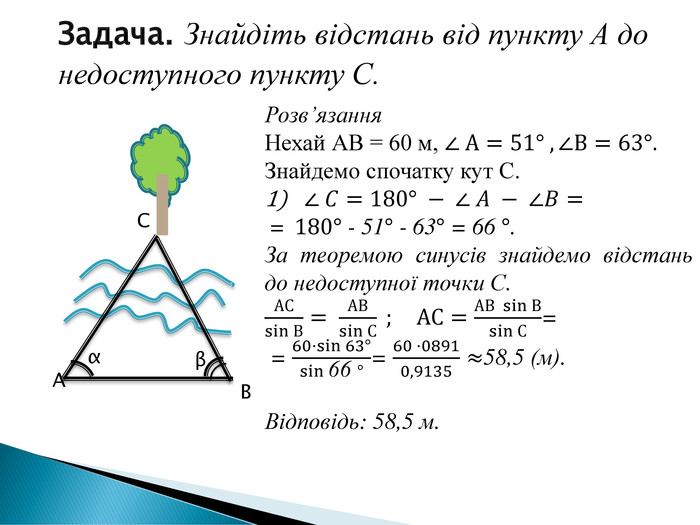
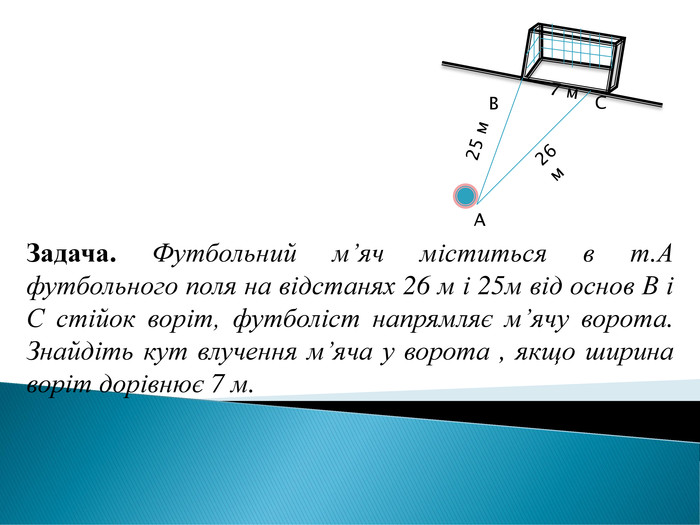
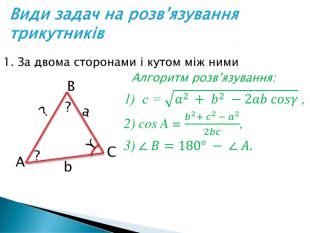
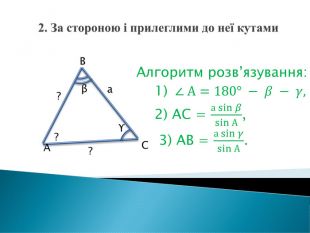
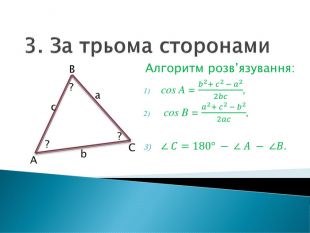
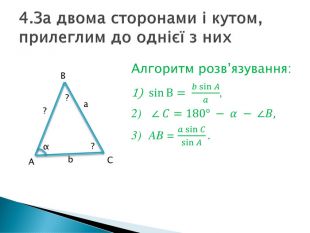
Розв'язування прикладних задач грунтується на розв'язування трикутників. Розглянемо приклади таких задач. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку